"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НЕСГЛАЖИВАЕМОЕ МНОГООБРАЗИЕ
Значение НЕСГЛАЖИВАЕМОЕ МНОГООБРАЗИЕ в математической энциклопедии:
- кусочно линейное или топологическое многообразие, не допускающее гладкой структуры.
Сглаживанием кусочно линейного многообразия Xназ. кусочно линейный изоморфизм  где М- гладкое многообразие. Многообразие, не допускающее сглаживания, и наз. несглаживаемым многообразием. Сказанное с нек-рыми изменениями применимо и к топологическим многообразиям.
где М- гладкое многообразие. Многообразие, не допускающее сглаживания, и наз. несглаживаемым многообразием. Сказанное с нек-рыми изменениями применимо и к топологическим многообразиям.
Пример Н. м. Пусть  - 4k-мерное многообразие Милнора (см. Древовидное многообразие). В частности,
- 4k-мерное многообразие Милнора (см. Древовидное многообразие). В частности,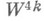 параллелизуемо, его сигнатура равна 8, и его край
параллелизуемо, его сигнатура равна 8, и его край  гомотопически эквивалентен сфере
гомотопически эквивалентен сфере  . Подклейка к
. Подклейка к  конуса
конуса  над
над  приводит к пространству
приводит к пространству  . При этом, так как Месть кусочно линейная сфера (см. обобщенная Пуанкаре гипотеза), то СМ кусочно линейный диск, так что Р- кусочно линейное многообразие. С другой стороны, Ресть Н. м., так как его сигнатура равна 8, а сигнатура гладкого почти параллелизуемого (т. е. параллелизуе-мого после выкалывания точки) 4-х мерного многообразия кратна числу
. При этом, так как Месть кусочно линейная сфера (см. обобщенная Пуанкаре гипотеза), то СМ кусочно линейный диск, так что Р- кусочно линейное многообразие. С другой стороны, Ресть Н. м., так как его сигнатура равна 8, а сигнатура гладкого почти параллелизуемого (т. е. параллелизуе-мого после выкалывания точки) 4-х мерного многообразия кратна числу  , экспоненциально растущему с ростом к. Многообразие Мне диффеоморфно сфере
, экспоненциально растущему с ростом к. Многообразие Мне диффеоморфно сфере  , т. е. М- Милнора сфера.
, т. е. М- Милнора сфера.
Критерий сглаживаемости кусочно линейного многообразия. Пусть  - ортогональная группа, а
- ортогональная группа, а  - группа сохраняющих начало кусочно линейных гомеоморфизмов
- группа сохраняющих начало кусочно линейных гомеоморфизмов  (см. Кусочно линейная топология). Включение
(см. Кусочно линейная топология). Включение  индуцирует расслоение
индуцирует расслоение 
 где BG- классифицирующее пространство группы G. При
где BG- классифицирующее пространство группы G. При  получается расслоение
получается расслоение 
 слой к-рого обозначается через М/О. Кусочно линейное многообразие Xобладает линейным стабильным нормальным расслоением
слой к-рого обозначается через М/О. Кусочно линейное многообразие Xобладает линейным стабильным нормальным расслоением  , классифицируемым отображением
, классифицируемым отображением  Если же Xявляется гладким (сглаживаемым) многообразием, то оно обладает векторным стабильным нормальным расслоением
Если же Xявляется гладким (сглаживаемым) многообразием, то оно обладает векторным стабильным нормальным расслоением  классифицируемым отображением
классифицируемым отображением  причем ро
причем ро  Это условие также и достаточно, т. е. замкнутое кусочно линейное многообразие Xсглаживаемо тогда и только тогда, когда его кусочно линейное стабильное нормальное расслоение допускает векторную редукцию, т. е. когда отображение
Это условие также и достаточно, т. е. замкнутое кусочно линейное многообразие Xсглаживаемо тогда и только тогда, когда его кусочно линейное стабильное нормальное расслоение допускает векторную редукцию, т. е. когда отображение  "поднимается" в ВО (существует такое
"поднимается" в ВО (существует такое  ).
).
Два сглаживания  и
и  наз. эквивалентными, если существует диффеоморфизм
наз. эквивалентными, если существует диффеоморфизм 
 (см. Структура на многообразии). Множество ts(X) классов эквивалентности сглаживаний находится в естественном взаимно однозначном соответствии с классами послойной гомотопности поднятий
(см. Структура на многообразии). Множество ts(X) классов эквивалентности сглаживаний находится в естественном взаимно однозначном соответствии с классами послойной гомотопности поднятий 
 отображения
отображения  . Иными словами, для сглаживаемого Xмножество
. Иными словами, для сглаживаемого Xмножество 
Лит.:[1] Kervaire M., "Comment, math, helv.", 1960, t. 34, p. 257-70; [2] Милнор Д ж., Сташеф Д ж., Характеристические классы, пер. с англ., М., 1979.
Ю. И. Рудяк.

 где М- гладкое многообразие. Многообразие, не допускающее сглаживания, и наз. несглаживаемым многообразием. Сказанное с нек-рыми изменениями применимо и к топологическим многообразиям.
где М- гладкое многообразие. Многообразие, не допускающее сглаживания, и наз. несглаживаемым многообразием. Сказанное с нек-рыми изменениями применимо и к топологическим многообразиям. - 4k-мерное многообразие Милнора (см. Древовидное многообразие). В частности,
- 4k-мерное многообразие Милнора (см. Древовидное многообразие). В частности,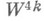 параллелизуемо, его сигнатура равна 8, и его край
параллелизуемо, его сигнатура равна 8, и его край  гомотопически эквивалентен сфере
гомотопически эквивалентен сфере  . Подклейка к
. Подклейка к  конуса
конуса  над
над  приводит к пространству
приводит к пространству  . При этом, так как Месть кусочно линейная сфера (см. обобщенная Пуанкаре гипотеза), то СМ кусочно линейный диск, так что Р- кусочно линейное многообразие. С другой стороны, Ресть Н. м., так как его сигнатура равна 8, а сигнатура гладкого почти параллелизуемого (т. е. параллелизуе-мого после выкалывания точки) 4-х мерного многообразия кратна числу
. При этом, так как Месть кусочно линейная сфера (см. обобщенная Пуанкаре гипотеза), то СМ кусочно линейный диск, так что Р- кусочно линейное многообразие. С другой стороны, Ресть Н. м., так как его сигнатура равна 8, а сигнатура гладкого почти параллелизуемого (т. е. параллелизуе-мого после выкалывания точки) 4-х мерного многообразия кратна числу  , экспоненциально растущему с ростом к. Многообразие Мне диффеоморфно сфере
, экспоненциально растущему с ростом к. Многообразие Мне диффеоморфно сфере  , т. е. М- Милнора сфера.
, т. е. М- Милнора сфера. - ортогональная группа, а
- ортогональная группа, а  - группа сохраняющих начало кусочно линейных гомеоморфизмов
- группа сохраняющих начало кусочно линейных гомеоморфизмов  (см. Кусочно линейная топология). Включение
(см. Кусочно линейная топология). Включение  индуцирует расслоение
индуцирует расслоение 
 где BG- классифицирующее пространство группы G. При
где BG- классифицирующее пространство группы G. При  получается расслоение
получается расслоение 
 слой к-рого обозначается через М/О. Кусочно линейное многообразие Xобладает линейным стабильным нормальным расслоением
слой к-рого обозначается через М/О. Кусочно линейное многообразие Xобладает линейным стабильным нормальным расслоением  , классифицируемым отображением
, классифицируемым отображением  Если же Xявляется гладким (сглаживаемым) многообразием, то оно обладает векторным стабильным нормальным расслоением
Если же Xявляется гладким (сглаживаемым) многообразием, то оно обладает векторным стабильным нормальным расслоением  классифицируемым отображением
классифицируемым отображением  причем ро
причем ро  Это условие также и достаточно, т. е. замкнутое кусочно линейное многообразие Xсглаживаемо тогда и только тогда, когда его кусочно линейное стабильное нормальное расслоение допускает векторную редукцию, т. е. когда отображение
Это условие также и достаточно, т. е. замкнутое кусочно линейное многообразие Xсглаживаемо тогда и только тогда, когда его кусочно линейное стабильное нормальное расслоение допускает векторную редукцию, т. е. когда отображение  "поднимается" в ВО (существует такое
"поднимается" в ВО (существует такое  ).
). и
и  наз. эквивалентными, если существует диффеоморфизм
наз. эквивалентными, если существует диффеоморфизм 
 (см. Структура на многообразии). Множество ts(X) классов эквивалентности сглаживаний находится в естественном взаимно однозначном соответствии с классами послойной гомотопности поднятий
(см. Структура на многообразии). Множество ts(X) классов эквивалентности сглаживаний находится в естественном взаимно однозначном соответствии с классами послойной гомотопности поднятий 
 отображения
отображения  . Иными словами, для сглаживаемого Xмножество
. Иными словами, для сглаживаемого Xмножество 