"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НЕРАЗВЕТВЛЕННЫЙ ХАРАКТЕРЗначение НЕРАЗВЕТВЛЕННЫЙ ХАРАКТЕР в математической энциклопедии:
- характер группы Галуа 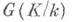 расширения Галуа локальных полей расширения Галуа локальных полей 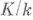 , тривиальный на подгруппе инерции. Любой Н. х. можно рассматривать как характер группы Галуа расширения , тривиальный на подгруппе инерции. Любой Н. х. можно рассматривать как характер группы Галуа расширения 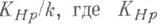 - максимальное неразветвленное подполе в расширении K/k. Н. х. образуют подгруппу в группе всех характеров. Неразветвленным характером наз. также характер мультипликативной группы - максимальное неразветвленное подполе в расширении K/k. Н. х. образуют подгруппу в группе всех характеров. Неразветвленным характером наз. также характер мультипликативной группы 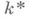 локального поля k, тривиальный на группе единиц поля k. Это определение согласовано с предыдущим, т. к. согласно основной теореме локальной теории полей классов для любого абе-лева расширения локальных полей К/к определен ка-нонич. гомоморфизм взаимности локального поля k, тривиальный на группе единиц поля k. Это определение согласовано с предыдущим, т. к. согласно основной теореме локальной теории полей классов для любого абе-лева расширения локальных полей К/к определен ка-нонич. гомоморфизм взаимности  , позволяющий отождествить характеры группы G(K/k )с нек-рой подгруппой в группе характеров группы k*. , позволяющий отождествить характеры группы G(K/k )с нек-рой подгруппой в группе характеров группы k*. Для расширения Галуа глобальных полей K/k характер 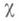 группы Галуа G(K/k )наз. неразветвленным в точке группы Галуа G(K/k )наз. неразветвленным в точке  поля к, если он остается неразветвленным в указанном выше смысле п при ограничении на подгруппу разложения любой точки поля к, если он остается неразветвленным в указанном выше смысле п при ограничении на подгруппу разложения любой точки 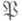 поля К, лежащей над поля К, лежащей над 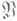 . Аналогично, характер . Аналогично, характер  группы классов иделей С(k)поля кназ. неразветвленным в группы классов иделей С(k)поля кназ. неразветвленным в  , если его ограничение на подгруппу единиц пополнения , если его ограничение на подгруппу единиц пополнения 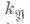 поля котносительно поля котносительно  тривиально, где группа тривиально, где группа  вложена стандартным образом в С(k). Из глобальной теории полей классов следует, что оба эти определения неразветвленности в точке вложена стандартным образом в С(k). Из глобальной теории полей классов следует, что оба эти определения неразветвленности в точке  согласованы, как и в локальном случае. согласованы, как и в локальном случае. Лит.:[1] Вейль А., Основы теории чисел, пер. с англ., М., 1972. Л. В. Кузьмин.
|

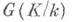 расширения Галуа локальных полей
расширения Галуа локальных полей 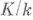 , тривиальный на подгруппе инерции. Любой Н. х. можно рассматривать как характер группы Галуа расширения
, тривиальный на подгруппе инерции. Любой Н. х. можно рассматривать как характер группы Галуа расширения 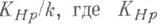 - максимальное неразветвленное подполе в расширении K/k. Н. х. образуют подгруппу в группе всех характеров. Неразветвленным характером наз. также характер мультипликативной группы
- максимальное неразветвленное подполе в расширении K/k. Н. х. образуют подгруппу в группе всех характеров. Неразветвленным характером наз. также характер мультипликативной группы 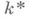 локального поля k, тривиальный на группе единиц поля k. Это определение согласовано с предыдущим, т. к. согласно основной теореме локальной теории полей классов для любого абе-лева расширения локальных полей К/к определен ка-нонич. гомоморфизм взаимности
локального поля k, тривиальный на группе единиц поля k. Это определение согласовано с предыдущим, т. к. согласно основной теореме локальной теории полей классов для любого абе-лева расширения локальных полей К/к определен ка-нонич. гомоморфизм взаимности  , позволяющий отождествить характеры группы G(K/k )с нек-рой подгруппой в группе характеров группы k*.
, позволяющий отождествить характеры группы G(K/k )с нек-рой подгруппой в группе характеров группы k*.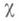 группы Галуа G(K/k )наз. неразветвленным в точке
группы Галуа G(K/k )наз. неразветвленным в точке  поля к, если он остается неразветвленным в указанном выше смысле п при ограничении на подгруппу разложения любой точки
поля к, если он остается неразветвленным в указанном выше смысле п при ограничении на подгруппу разложения любой точки 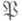 поля К, лежащей над
поля К, лежащей над 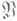 . Аналогично, характер
. Аналогично, характер  группы классов иделей С(k)поля кназ. неразветвленным в
группы классов иделей С(k)поля кназ. неразветвленным в  , если его ограничение на подгруппу единиц пополнения
, если его ограничение на подгруппу единиц пополнения 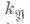 поля котносительно
поля котносительно  тривиально, где группа
тривиально, где группа  вложена стандартным образом в С(k). Из глобальной теории полей классов следует, что оба эти определения неразветвленности в точке
вложена стандартным образом в С(k). Из глобальной теории полей классов следует, что оба эти определения неразветвленности в точке  согласованы, как и в локальном случае.
согласованы, как и в локальном случае.