"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НЕРАЗВЕТВЛЕННЫЙ ИДЕАЛЗначение НЕРАЗВЕТВЛЕННЫЙ ИДЕАЛ в математической энциклопедии:
- простой идеал 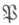 поля алгебраич. чисел К, лежащий над таким простым числом р, что главный идеал (р) имеет в поле Кразложение в произведение простых идеалов вида поля алгебраич. чисел К, лежащий над таким простым числом р, что главный идеал (р) имеет в поле Кразложение в произведение простых идеалов вида 
причем 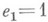 . Точнее этот идеал наз. абсолютно неразветвленным. В общем случае, пусть А- дедекиндово кольцо с полем частных к, К - конечное расширение поля k и В- целое замыкание Ав К. Простой идеал . Точнее этот идеал наз. абсолютно неразветвленным. В общем случае, пусть А- дедекиндово кольцо с полем частных к, К - конечное расширение поля k и В- целое замыкание Ав К. Простой идеал  кольца В, лежащий над идеалом кольца В, лежащий над идеалом  кольца А, наз. неразветвленным в расширении K/k, если кольца А, наз. неразветвленным в расширении K/k, если 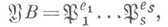
где  - попарно различные простые идеалы кольца В, - попарно различные простые идеалы кольца В,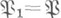 и e1=1. Если все идеалы и e1=1. Если все идеалы  не разветвлены, то иногда говорят, что идеал не разветвлены, то иногда говорят, что идеал 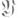 остается неразветвленным в Klk. Для расширения Галуа Klk неразветвленность идеала остается неразветвленным в Klk. Для расширения Галуа Klk неразветвленность идеала  кольца Вэквивалентна тому, что подгруппа разложения кольца Вэквивалентна тому, что подгруппа разложения  в группе Галуа G(K/k )совпадает с группой Галуа расширения полей вычетов в группе Галуа G(K/k )совпадает с группой Галуа расширения полей вычетов  . В любых конечных расширениях полей алгебраич. чисел все идеалы, кроме конечного числа, не разветвлены. . В любых конечных расширениях полей алгебраич. чисел все идеалы, кроме конечного числа, не разветвлены. Лит.:[1] Боревич 3. И., Шафаревич И. Р., Теория чисел, 2 изд., М., 1972; [2] Ленг С, Алгебраические числа, пер. с англ., М., 1966; [3] Алгебраическая теория чисел, пер. с англ., М., 1969. Л. В. Кузьмин.
|

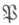 поля алгебраич. чисел К, лежащий над таким простым числом р, что главный идеал (р) имеет в поле Кразложение в произведение простых идеалов вида
поля алгебраич. чисел К, лежащий над таким простым числом р, что главный идеал (р) имеет в поле Кразложение в произведение простых идеалов вида
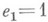 . Точнее этот идеал наз. абсолютно неразветвленным. В общем случае, пусть А- дедекиндово кольцо с полем частных к, К - конечное расширение поля k и В- целое замыкание Ав К. Простой идеал
. Точнее этот идеал наз. абсолютно неразветвленным. В общем случае, пусть А- дедекиндово кольцо с полем частных к, К - конечное расширение поля k и В- целое замыкание Ав К. Простой идеал  кольца В, лежащий над идеалом
кольца В, лежащий над идеалом  кольца А, наз. неразветвленным в расширении K/k, если
кольца А, наз. неразветвленным в расширении K/k, если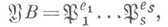
 - попарно различные простые идеалы кольца В,
- попарно различные простые идеалы кольца В,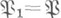 и e1=1. Если все идеалы
и e1=1. Если все идеалы  не разветвлены, то иногда говорят, что идеал
не разветвлены, то иногда говорят, что идеал 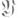 остается неразветвленным в Klk. Для расширения Галуа Klk неразветвленность идеала
остается неразветвленным в Klk. Для расширения Галуа Klk неразветвленность идеала  кольца Вэквивалентна тому, что подгруппа разложения
кольца Вэквивалентна тому, что подгруппа разложения  в группе Галуа G(K/k )совпадает с группой Галуа расширения полей вычетов
в группе Галуа G(K/k )совпадает с группой Галуа расширения полей вычетов  . В любых конечных расширениях полей алгебраич. чисел все идеалы, кроме конечного числа, не разветвлены.
. В любых конечных расширениях полей алгебраич. чисел все идеалы, кроме конечного числа, не разветвлены.