|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НЕПРЕРЫВНОСТИ МОДУЛЬЗначение НЕПРЕРЫВНОСТИ МОДУЛЬ в математической энциклопедии: - одна из основных характеристик непрерывных функций. Н. м. непрерывной на отрезке функции
Определение Н. м. введено А. Лебегом (A. Lebesgue) в 1910, хотя по существу понятие было известно и ранее. Если Н. м. функции
где
где
- конечная разность k-го порядка функции f(x), иН. м. в произвольных пространствах функций, напр, интегральный Н. м. функции
Для Лит.:[1] Зигмунд А., Тригонометрические ряды, пер. с англ., [2 изд.], т. 1, М., 1965; [2] Ахиезер Н. И., Лекции по теории аппроксимации, 2 изд., М., 1965; [3] Дзядык В. К., Вьедение в теорию равномерного приближения функций полиномами, М., 1977. Л. В. Ефимов. |
|
|
|

 определяется как
определяется как
 удовлетворяет условию
удовлетворяет условию
 , то говорят, что функция
, то говорят, что функция  удовлетворяет Липшица условию порядка
удовлетворяет Липшица условию порядка  Для того чтобы неотрицательная функция
Для того чтобы неотрицательная функция  была Н. м. нек-рой непрерывной функции, необходимо и: достаточно, чтобы она обладала следующими свойствами:
была Н. м. нек-рой непрерывной функции, необходимо и: достаточно, чтобы она обладала следующими свойствами:  не убывает,
не убывает,  непрерывна,
непрерывна,  Рассматриваются также Н. м. высших порядков
Рассматриваются также Н. м. высших порядков
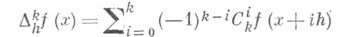
 , интегрируемой на отрезке
, интегрируемой на отрезке  со степенью
со степенью 

 -периодической функции интеграл в выражении (*) берется по отрезку [0,
-периодической функции интеграл в выражении (*) берется по отрезку [0, ].
].