|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НЕПРЕРЫВНОЕ ОТОБРАЖЕНИЕЗначение НЕПРЕРЫВНОЕ ОТОБРАЖЕНИЕ в математической энциклопедии: - отображение а) прообраз б) прообраз в) Понятие непрерывной функции, корректно сформулированное еще Б. Больцано (В. Bolzano) и О. Коши (A. Cauchy), сыграло большую роль в математике 19 в. Функция Вейерштрасса, не дифференцируемая ни в одной точке, "канторовская лестница", кривая Пеано указали на необходимость рассмотрения более частных случаев непрерывности. Необходимость выделения специальных классов Н. о. еще более возросла, когда стали рассматривать Н. о. более общих объектов - топологич. пространств. Можно отметить следующие важнейшие типы Н. о.: топологич. отображения или гомеоморфизмы, совершенные отображения, замкнутые отображения, открытые отображения, факторные отображения. Если даны два Н. о. Эти общие формулировки охватывают, в частности, следующий вопрос: какие топологич. свойства сохраняются теми или иными отображениями при переходе от пространства к его образу или прообразу. 1) Всякое n-мерное в смысле dim пространство может быть существенно отображено (см. Существенное отображение )на re-мерный куб. 2) Точечно-счетная база сохраняется при совершенных (даже при бифакторных) отображениях. 3) Всякое замкнутое отображение f из класса Hom Первые конкретные задачи этого рода были решены более полувека назад. Таковы, напр., представление произвольного компакта в виде непрерывного образа канторова совершенного множества (теорема Александрова); характеристика метрич. пространств со счетной базой как открытых непрерывных образов подпространств пространства иррациональных чисел (теорема Хаусдорфа); описание локально связных континуумов как непрерывных образов отрезка. Решение этих задач не только позволило ответить на вопросы о взаимоотношениях между различными известными ранее классами пространств, но и вызвало появление новых интересных классов пространств. Таковы, напр., диадические бикомпакты, паракомпактные р-пространства, совершенно n-мерные пространства, псевдокомпактные пространства. Понятие действительной непрерывной функции, т. е. Н. о. топология, пространства в Существенную часть теории размерности составляет изучение поведения размерностных характеристик пространств при переходе к образу или прообразу относительно отображений тех или иных классов. Большую роль здесь играют Одной из характеристик размерности является возможность продолжения с замкнутого подмножества Н. о. в re-мерную сферу. Эта теорема является одним из вариантов теоремы о продолжении отображений, которая, как и тесно связанная с ней теорема о неподвижной точке, имеет кардинальное значение для таких разделов современной математики, как топология, алгебра, теория функций и функциональный анализ, дифференциальные уравнения. Одним из наиболее изученных классов Н. о. является класс совершенных неприводимых отображений. Теорема об абсолюте регулярного пространства породила целый ряд исследований в этой области. В частности, понятие абсолюта было распространено на класс всех хаусдорфовых пространств. С понятием Н. о. оказалось тесно связанным понятие Выделение равномерно непрерывных функций из класса всех числовых функций одной или нескольких действительных переменных стало одной из отправных точек исследований, приведших к созданию равномерной топологии. Н. о. того или иного типа лежат в основе теории ретрактов, спайнов, гомологии. Большую роль в современной математике играют различные аспекты теории многозначных отображений. Интересны богатством идейного содержания вопросы Н. о. евклидовых пространств. Лит.:[1] Александров П. С, Введение в теорию множеств и общую топологию, М., 1977; [2] Бурбаки Н., Общая топология. Основные структуры, пер. с франц., М., 1968; [3] Келли Дж, Общая топология, пер. с англ., 2 изд., М., 1981; [4] Архангельский А. В., Пономарев В. И, Основы общей топологии в задачах и упражнениях, М., 1974; [5] Александрян Р. А., Мирзаханян Э. А., Общая топология, М., 1979. В. В. Федорчук. |
|
|
|

 топологич. пространства Xв топологич. пространство У такое, что для всякой точки
топологич. пространства Xв топологич. пространство У такое, что для всякой точки  и для всякой окрестности
и для всякой окрестности  ее образа f(x0) существует такая окрестность
ее образа f(x0) существует такая окрестность  точки х 0 , что
точки х 0 , что  Это определение является перефразировкой окрестност-ного определения непрерывности функций действительного переменного (см. Непрерывная функция). Существует много эквивалентных определений непрерывности. Так, для непрерывности отображения
Это определение является перефразировкой окрестност-ного определения непрерывности функций действительного переменного (см. Непрерывная функция). Существует много эквивалентных определений непрерывности. Так, для непрерывности отображения  необходимо и достаточно, чтобы выполнялось любое из следующих условий:
необходимо и достаточно, чтобы выполнялось любое из следующих условий: всякого открытого в Y множества Gоткрыт в X;
всякого открытого в Y множества Gоткрыт в X; всякого замкнутого в Y множества Fзамкнут в X;
всякого замкнутого в Y множества Fзамкнут в X; для всякого множества
для всякого множества  (образ замыкания содержится в замыкании образа).
(образ замыкания содержится в замыкании образа). то их композиция
то их композиция 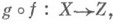 т. е. сквозное отображение
т. е. сквозное отображение  непрерывна. Очевидно непрерывно и всякое тождественное отображение
непрерывна. Очевидно непрерывно и всякое тождественное отображение  . Поэтому топологич. пространства и Н. о. образуют категорию. Одним из методов топологии является метод взаимной классификации пространств и отображений. Его сущность состоит в следующем: выделяются три основные, тесно связанные между собой задачи. 1) В каком случае каждое пространство нек-рого фиксированного класса
. Поэтому топологич. пространства и Н. о. образуют категорию. Одним из методов топологии является метод взаимной классификации пространств и отображений. Его сущность состоит в следующем: выделяются три основные, тесно связанные между собой задачи. 1) В каком случае каждое пространство нек-рого фиксированного класса  может быть отображено на нек-рое пространство класса
может быть отображено на нек-рое пространство класса  посредством Н. о., принадлежащего классу
посредством Н. о., принадлежащего классу  ? 2) Какими внутренними свойствами характеризуются пространства, принадлежащие классам МС, являющимся образами пространств из класса Спри Н. о. из класса M?3) Пусть
? 2) Какими внутренними свойствами характеризуются пространства, принадлежащие классам МС, являющимся образами пространств из класса Спри Н. о. из класса M?3) Пусть  - обозначение множества Н. о., областью определения к-рых служат пространства из класса
- обозначение множества Н. о., областью определения к-рых служат пространства из класса  , а областью значений - пространства из класса
, а областью значений - пространства из класса  - нек-рый другой класс отображений. Каковы свойства отображений из класса
- нек-рый другой класс отображений. Каковы свойства отображений из класса  ?
? , где
, где  - класс n-мерных пространств со счетной базой,
- класс n-мерных пространств со счетной базой,  - класс нульмерных пространств со счетной базой, по крайней мере (n+1)-кратно.
- класс нульмерных пространств со счетной базой, по крайней мере (n+1)-кратно. , лежащее в основании теории функций, играет большую роль и в общей топологии. Здесь прежде всего стоит отметить Урысона лемму, теорему Брауэра - Урысона о продолжении непрерывных функций с замкнутых подмножеств нормальных пространств, определение А. Н. Тихоновым вполне регулярных пространств, Вейерштрасса- Стоуна теорему. Эти и другие исследования привели к созданию теории колец непрерывных функций, методы к-рой оказались достаточно плодотворными в общей топологии.
, лежащее в основании теории функций, играет большую роль и в общей топологии. Здесь прежде всего стоит отметить Урысона лемму, теорему Брауэра - Урысона о продолжении непрерывных функций с замкнутых подмножеств нормальных пространств, определение А. Н. Тихоновым вполне регулярных пространств, Вейерштрасса- Стоуна теорему. Эти и другие исследования привели к созданию теории колец непрерывных функций, методы к-рой оказались достаточно плодотворными в общей топологии. -сдвиги,
-сдвиги,  -отображения и w-отображения, существенные отображения, конечно-кратные отображения, счетнократные отображения, нульмерные отображения, n-мерные отображения и др. При этом метод Н. о. приводит к взаимному обогащению и проникновению друг в друга таких совершенно различных по своему происхождению областей общей топологии, как имеющая наглядно-геометрич. смысл теория размерности и абстрактная по характеру теория кардинальнозначных инвариантов.
-отображения и w-отображения, существенные отображения, конечно-кратные отображения, счетнократные отображения, нульмерные отображения, n-мерные отображения и др. При этом метод Н. о. приводит к взаимному обогащению и проникновению друг в друга таких совершенно различных по своему происхождению областей общей топологии, как имеющая наглядно-геометрич. смысл теория размерности и абстрактная по характеру теория кардинальнозначных инвариантов. -близости, к-рое дало возможность внутреннего описания всех совершенных неприводимых прообразов произвольного бикомпакта. Распространение теории неприводимых Н. о. на класс всех хаусдорфовых пространств показало, что Н. о. не хватает для изучения нерегулярных пространств и что более естественно здесь рассматривать
-близости, к-рое дало возможность внутреннего описания всех совершенных неприводимых прообразов произвольного бикомпакта. Распространение теории неприводимых Н. о. на класс всех хаусдорфовых пространств показало, что Н. о. не хватает для изучения нерегулярных пространств и что более естественно здесь рассматривать  -непрерывные отображения.
-непрерывные отображения.