|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НЕПРАВИЛЬНОСТИ КОЭФФИЦИЕНТЫЗначение НЕПРАВИЛЬНОСТИ КОЭФФИЦИЕНТЫ в математической энциклопедии: линейной системы обыкновенных дифференциальных уравнений - неотрицательные функции s(А), равные нулю в том и только в том случае, если система
где 1) Коэффициент неправильности Ляпунова [1]
где 2) Коэффициент неправильности IIеррона [2]
где Если система (*) есть система уравнений в вариациях гамильтоновой системы
поэтому для правильности системы уравнений в вариациях гамильтоновой системы необходимо и достаточно, чтобы Лит.:[1] Ляпунов А. М., Собр. соч., т. 2, М., 1956; [2] Реrrоn О., "Math. Z.", 1929/1930, Bd 31, S. 748-66; [3] Малкин И. Г., Теория устойчивости движения, 2 изд., М., 1966, § 79; [4] Былов Б. Ф., Виноград Р. Э., Гробман Д. М., Немыцкий Б. В., Теория показателей Ляпунова,.., М., 1966; [5] Изобов Н. А., в кн.: Итоги науки и техники. Математический анализ, т. 12, М., 1974, с. 71-146; [6] Прохорова Р. А., "Дифференц. уравнения", 1976, т. 12, № 3, с. 475-83; №4, с. 760-69. В. М. Миллионщиков. |
|
|
|
- суммируемое на каждом отрезке отображение 
,- правильная линейная система. Наиболее известны (и наиболее просто определяются) следующие Н. к.
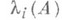- Ляпунова характеристические показа тели системы (*), занумерованные в порядке невозрастания, a tr A(t)- след отображения A(t).
- отображение, сопряженное к A(t).
(теорема Персидского) Имеются также другие Н. к. (см. [4] - [61).