|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НЕОПРЕДЕЛЕННЫХ КОЭФФИЦИЕНТОВ МЕТОДЗначение НЕОПРЕДЕЛЕННЫХ КОЭФФИЦИЕНТОВ МЕТОД в математической энциклопедии: построения численных алгоритмов - специальный метод построения алгоритмов, основанный на требовании, чтобы алгоритм был точен или имел погрешность определенного порядка точности на нек-ром множестве задач. Типичным примером задач, к-рые наряду с другими методами могут решаться Н. к. м., являются следующие (см. [1], [2]). Известны значения функции
формулу для вычисления производной:
формулу для вычисления интеграла:
Для решения последней из этих задач задаются нек-рой формой приближенного решения, напр, линейной
и определяют коэффициенты
где
выполнялось при всех
Отсюда определяют (если это возможно) искомые
В случае формул численного интегрирования в качестве неизвестных параметров часто выступают и координаты узлов интегрирования. Напр., в квадратурных формулах Гаусса вида
рассматриваются как свободные параметры координаты узлов Особенно широко Н. к. м. используется при построении аппроксимаций уравнений с частными производными (см. [3]). Лит.:[1] Березин И. С, Жидков Н. П., Методы вычислений, 3 изд., т. 1, М., 1966; 2 изд., т. 2, М., 1962; [2] Бахвалов Н. С, Численные методы, 2 изд., М., 1975; [3] Годунов С. К., Рябенький В. С, Разностные схемы. Введение в теорию, 2 изд., М., 1977. Н. С. Бахвалов. |
|
|
|


 . Требуется построить формулу для приближения функции:
. Требуется построить формулу для приближения функции:



 из требования, чтобы приближенная формула
из требования, чтобы приближенная формула  была точной для функций из нек-рой совокупности, напр, вида
была точной для функций из нек-рой совокупности, напр, вида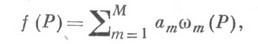
 фиксированы,
фиксированы,  произвольны. Как правило, берут
произвольны. Как правило, берут  . Чтобы равенство
. Чтобы равенство
 , достаточно выполнения соотношений
, достаточно выполнения соотношений
 Иногда задаются более сложной формой зависимости. Напр., при приближении функций часто известно, что рассматриваемая функция хорошо приближается функциями вида
Иногда задаются более сложной формой зависимости. Напр., при приближении функций часто известно, что рассматриваемая функция хорошо приближается функциями вида  где
где  неизвестны. Параметры а т подбирают из системы уравнений
неизвестны. Параметры а т подбирают из системы уравнений

 ; благодаря этому удается построить квадратуры, точные для многочленов степени
; благодаря этому удается построить квадратуры, точные для многочленов степени  . При конструировании аппроксимаций дифференциальных уравнений с помощью Н. к. м. требуют, чтобы при подстановке в конечноразностную схему решения задачи получалась величина рассогласования (невязка )требуемого порядка малости по отношению к шагу сетки. Такой прием положен в основу способов построения методов Рунге - Кутта и конечноразностных методов (см. [1], [2]).
. При конструировании аппроксимаций дифференциальных уравнений с помощью Н. к. м. требуют, чтобы при подстановке в конечноразностную схему решения задачи получалась величина рассогласования (невязка )требуемого порядка малости по отношению к шагу сетки. Такой прием положен в основу способов построения методов Рунге - Кутта и конечноразностных методов (см. [1], [2]).