|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НЕЛИНЕЙНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИЗначение НЕЛИНЕЙНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ в математической энциклопедии: - уравнение вида
где Из существенно нелинейных уравнений наиболее известным является Монжа- Ампера уравнение
здесь и ниже Если
с, производная дu/дp22 имеет вес равный двум. Так как линеаризация уравнения (1) относительно старших производных проводится в окрестности фиксированного решения, то в отличие от линейного уравнения тип уравнения (1) (даже в фиксированной точке х)может зависеть от этого фиксируемого решения. Напр., уравнение
является уравнением эллиптич. типа на решениях с с Тип уравнения определяет постановку корректных краевых (смешанных) задач для этого уравнения и методы их исследования. Если функция Fявляется линейной относительно старших производных, то уравнение (1) наз. квазилинейным уравнением. Напр., уравнение (3) является квазилинейным уравнением. В противном случае уравнение наз. существенно нелинейным уравнением. Напр., уравнение Мон-жа - Ампера (2) является существенно нелинейным. Если коэффициенты квазилинейного уравнения при старших производных не зависят от искомого решения (и его производных), то это уравнение наз. слабо нелинейным уравнением. Напр., уравнение
является слабо нелинейным уравнением. Разделение Н. у. с ч. п. на квазилинейные и слабо нелинейные носит условный характер и не отражает внутреннего существа самих уравнений. Слабо нелинейное уравнение может обладать более сильными нелинейными свойствами, нежели квазилинейное и даже существенно нелинейное уравнение. Напр., существуют слабо нелинейные уравнения вида (4), к-рые при заданном граничном условии Дирихле в ограниченной области обладают счетным множеством разных решений. Уравнения вида (1) могут рассматриваться во всем пространстве Н. у. с ч. п. вместе с граничным условием (условиями) порождает нелинейную задачу. Эта нелинейная задача рассматривается в соответствующем пространстве функций. Выбор этого функционального пространства решений определяется структурой нелинейного дифференциального оператора F, задаваемого в области, и структурой граничных операторов. Выбор функционального пространства для нелинейной задачи является существенным моментом при исследовании этой задачи. Напр., нелинейной задаче
в ограниченной области При исследовании задач для Н. у. с ч. <п. рассматриваются вопросы о существовании решения, о числе решений, об отсутствии решения, о разрушении решения, о бифуркации (ветвлении) решения, об асимптотике решения при аргументе, стремящемся к границе, в частности к бесконечности, в случае неограниченных областей. Теория таких задач имеет два аспекта: локальный и глобальный. Локальная теория относительно полно развита для общих нелинейных задач, принадлежащих либо к эллиптич. типу, либо к параболич. типу, либо к гиперболич. типу. Эта теория основана на теореме о неявной функции из нелинейного функционального анализа и общей теории линейных задач соответствующего типа. В случае краевых (смешанных) задач для нелинейных параболич. либо гиперболич. уравнений эта локальная теория позволяет установить разрешимость задачи либо на достаточно малом временном промежутке, либо на фиксированном временном промежутке при условии достаточно малого отклонения (в соответствующей метрике) данных задачи от данных известного решения (как правило нулевого решения) близкой задачи. Глобальная теория нелинейных задач развита менее полно и только для отдельных классов уравнений. Нелинейные уравнения с частными производными первого порядка. Для широкого класса квазилинейных скалярных уравнений первого порядка вида
установлена теорема существования и единственности решения задачи Коши с начальным условием при t=0 для всех t>0. Для более узкого класса уравнений вида (5) рассмотрены также вопросы асимптотики решений таких задач при Теория систем квазилинейных уравнений с частными производными первого порядка развита менее полно (см. Квазилинейные гиперболические уравнения и систем ы). Нелинейные уравнения с частными производными второго порядка. Уравнения эллиптич. типа и парабол и ч. т и п а. Относительно полно развита теория разрешимости в целом краевых задач для широкого класса квазилинейных скалярных уравнений эллиптич. типа второго порядка, имеющих вид
либо
при условии существования априорной оценки Аналогично положение и с теорией разрешимости в целом краевых (смешанных) задач для широкого класса квазилинейных скалярных уравнений параболич. типа второго порядка, имеющих вид
либо
Эта теория разрешимости основана на теории априорных оценок и методе Лере - Шаудера. Получение априорной исходной оценки Разрешимость в целом краевой (смешанной) задачи для существенно нелинейных скалярных уравнений параболич. типа установлена для широкого класса уравнений параболич. типа вида
в случае одной пространственной переменной Вопросы разрешимости в целом задач для систем квазилинейных уравнений эллиптич. типа либо параболич. типа рассмотрены для отдельных узких классов таких систем. Одним из эффективных методов в исследовании Н. у. с ч. п. второго порядка, принадлежащих либо к эллиптич., либо к параболич. типу, является метод верхних и нижних решений. Напр., пусть поставлена краевая задача
с непрерывной функцией f, определенной на
при всех Исследование поведения в целом решений краевых (смешанных) задач для нелинейных параболич. уравнений, как и в случае обыкновенных дифференциальных уравнений, связано с исследованием стационарных решений краевых задач для соответствующих не-лпнейных эллиптич. уравнений. В связи с тем, что краевые задачи для нелинейных эллиптич. уравнений не всегда имеют решение и для краевых (смешанных) задач для нелинейных параболич. и гиперболич. уравнений не при всех t>0 существует решение, развивается теория отсутствия решений задач для Н. у. с ч. п. Уравнения гиперболич. типа. Эти уравнения занимают особое место среди Н. у. с ч. п. второго порядка. "Потеря одной производной" при обращении гиперболич. оператора второго порядка приводит к принципиальным трудностям при исследовании нелинейных гиперболич. уравнений. Даже для создания локальной теории нелинейных гиперболич. уравнений и систем потребовалось развитие специальной теории о неявных функциях в нелинейном функциональном анализе, так как классич. теорема о неявной функции из функционального анализа оказалась здесь неприменимой. Для (существенно) квазилинейных гиперболич. уравнений второго порядка с числом независимых переменных больше двух вопрос о разрешимости в целом даже задачи Коши не исследован. В случае двух независимых переменных (
сводимых к специальным квазилинейным гиперболич. системам - законам сохранения (см. Квазилинейные гиперболические уравнения и системы). В случае квазилинейных гиперболич. уравнений вида
установлена разрешимость в целом (для любого T>0) смешанной задачи с условиями: u=0 на
Разрешимость в целом задачи Коши, а также краевой (смешанной) задачи установлена для широкого класса слабо нелинейных гиперболич. уравнений вида
Особое место в теории нелинейных гиперболич. уравнений занимает вопрос о существовании периодических по tрешений краевых задач для этих уравнений. Даже для слабо нелинейных уравнений этот вопрос рассмотрен только для уравнений вида
в случае двух переменных
При этом относительно функций
для уравнения (11) достаточно выполнение условий: 1) Функции
с
2) Выполнено следующее условие коэрцитивности: для любой функции
3) Выполнено условие монотонности: для любых функций
Тогда при выполнении условий 1) -3) краевая задача (12) для уравнения (11) при любой функции f из сопряженного пространства
Все эти условия можно существенно расширить. Напр., для дифференциальных операторов вида (11) с граничными условиями (12), к-рые являются нечетными и однородными в главном при нек-рых условиях, но без условия коэрцитивности, справедлива альтернатива Фредгольма: если соответствующая краевая задача с нулевыми граничными условиями (12) для уравнения (11) с f=0 имеет только тривиальное решение, то эта задача разрешима при любой функции f из соответствующего сопряженного пространства. Для широкого класса краевых (смешанных) задач для Н. у. с ч. п. развита теория нормальной разрешимости, к-рая обобщает теорию нормальной разрешимости (по Хаусдорфу) линейных операторных уравнений на нелинейный случай. Эта теория дает достаточные условия разрешимости краевых (смешанных) задач для нелинейных уравнений и систем уравнений парабо-лич. типа и для слабо нелинейных уравнений и систем гиперболич. типа. В теории краевых задач для нелинейных уравнений эллиптич. типа особое место занимает вопрос о существовании собственных функций. Теория собственных функций краевых задач для квазилинейных уравнений эллиптич. типа развита для достаточно широкого класса задач. В частности, на широкий класс задач перенесена абстрактная теория Люстерника - Шнирельмана о существовании счетного множества собственных функций. Особое место в теории нелинейных уравнений эллиптич. типа высшего порядка и в теории систем нелинейных уравнений эллиптич. типа с числом независимых переменных, большим двух, занимает вопрос о регулярности решений этих уравнений и систем. В случае скалярного квазилинейного равномерно эллиптич. уравнения второго порядка с достаточно гладкими коэффициентами, удовлетворяющими вместе со своими первыми производными определенным условиям роста, решение обладает гладкостью внутри области на две производные, превышающие гладкость правой части из соответствующего пространства. В случае квазилинейных уравнений эллиптич. типа порядка выше двух и систем квазилинейных уравнений эллиптич. типа второго либо более высокого порядка с числом независимых переменных, большим двух, соответствующая гладкость решений имеет место не всюду внутри области, а почти всюду. При дополнительных условиях удается уточнить размерность этой нулевой (хаусдорфовой) меры, на множествах к-рой, вообще говоря, гладкость решений теряется. Для специального класса квазилинейных эллиптич. систем с ограниченными нелинейностями установлена регулярность решений всюду в области. Развита теория краевых задач для широкого класса квазилинейных уравнений дивергентного вида бесконечного порядка. Теория точных решений. К методам точных решений относятся: метод, основанный на групповом анализе Н. у. с ч. п.; метод, основанный на преобразованиях Ли - Беклунда; метод, основанный на обратной задаче теории рассеяния, и нек-рые др. Метод обратной задачи рассеяния позволил исследовать ряд физически важных уравнений, таких, как нелинейные уравнения Кортевега - де Фриса:
нелинейное уравнение синус-Гордона:
нелинейное уравнение Шрёдингера:
и ряд других с одной пространственной переменной Лит.:[1] Курант Р., Уравнения с частными производными, пер. с англ., М., 1964; [2] Ладыженская О. А., Уральцева Н. Н., Линейные и квазилинейные уравнения эллиптического типа, 2 изд., М., 1973; [3] Gilbarg D., Trudinger N. S., Elliptic Partial Differential Equations of Second Order, В.- N. Y., 1977; [4] Ладыженская О. А., Солонников В. А., Уральцева Н. Н., Линейные и квазилинейные уравнения параболического типа, М., 19В7; [5] Фридман А., Уравнения с частными производными параболического типа, пер. с англ., М., 1968; [6] Ниренберг Л., Лекции по нелинейному функциональному анализу, пер. с англ., М., 1977; [7] Лионе Ж.-Л., Некоторые методы решения нелинейных краевых задач, пер. с франц., М., 1972; [8] Рождественский Б. Л., Яненко Н. Н., Системы квазилинейных уравнений..., М., 1978; [9] Скрипник И. В., Нелинейные эллиптические уравнения высшего порядка, К., 1973: [10] Pucik S., Netas J., Sоucеk J., Soucek V., Spectral Analysis of Nonlinear Operators, В., 1973: [11] Овсянников Л. В., Групповой анализ дифференциальных уравнений, М., 1978; [12] Захаров В. Е., Манаков С. В., Новиков С. П., Питаевский Л. П., Теория солитонов. Метод обратной задачи, М., 1080: [13] Вишик М. И., "Тр. Моск. матем. об-ва", 1003, т. 12, с. 125-64; [14] Giaquinta M., Modica G., "Manuscripta math.", 1979, v. 28, № 1-3, p. 109-58; [15] Дубинский Ю. А., "Матем. сб.", 1975, т. 98, .№ 2, с. 163-84; [16] Kazdan J. L., Kramer R., "Comm. pure and appl. Math.", 1978, v. 31, MS 5, p. 619-45; [17] Кoшелев А. И., "Успехи матем. наук", 1978, т. 33, в. 4, с. 3-49; [18] Кружков С. Н., "Матем. сб.", 1970, т. 81, № 2, с. 228-55: [19] его же, "Тр. Моск. матем. об-ва", 1967, т. 16, с. 329-46; [20] Олейник О. А., "Успехи матем. наук", 1959, т. 14, в. 2, с. 165 - 70; [21] Похожаев С. И., "Матем. сб.", 1970, т. 82, № 2, с. 192-212; [22] его же, "Матем. сб.", 1975, т. 90, № 1, с. 152-66; [23] его же,. "Матем. сб.", 1980, т. 113, № 2, с. 324-38. С. И. Похожаев. |
|
|
|




 есть мультииндекс с целыми неотрицательными
есть мультииндекс с целыми неотрицательными 
 где.
где.  Аналогично определяется Н. у. <с ч. п. в случае комплекснозначных функций. Если k>l, то векторное Н. у. с ч. п. обычно наз. системой Н. у. о ч. п. Порядком уравнения (1) наз. наивысший порядок производной, входящей в это уравнение.
Аналогично определяется Н. у. <с ч. п. в случае комплекснозначных функций. Если k>l, то векторное Н. у. с ч. п. обычно наз. системой Н. у. о ч. п. Порядком уравнения (1) наз. наивысший порядок производной, входящей в это уравнение.
 .
. и функция Fдифференцируема относительно своих "старших" переменных, соответствующих старшим производным, то тип уравнения (2) определяется типом главной линейной относительно старших производных частью функции F(см. Дифференциальное уравнение с частными производными). При этом производным по соответствующим переменным, либо соответствующим дифференциальным операциям, в общем случае, присваивается соответствующий определенный вес. Напр., в нелинейном уравнении теплопроводности
и функция Fдифференцируема относительно своих "старших" переменных, соответствующих старшим производным, то тип уравнения (2) определяется типом главной линейной относительно старших производных частью функции F(см. Дифференциальное уравнение с частными производными). При этом производным по соответствующим переменным, либо соответствующим дифференциальным операциям, в общем случае, присваивается соответствующий определенный вес. Напр., в нелинейном уравнении теплопроводности


 и уравнением гиперболич. типа на решениях
и уравнением гиперболич. типа на решениях

 либо в нек-рой области этого пространства. В первом случае функциональный класс решений включает условия поведения решений на бесконечности. В случае области на границе этой области либо на части ее ставятся определенные граничные условия либо одно граничное условие. Эти граничные условия также могут содержать нелинейные операторы.
либо в нек-рой области этого пространства. В первом случае функциональный класс решений включает условия поведения решений на бесконечности. В случае области на границе этой области либо на части ее ставятся определенные граничные условия либо одно граничное условие. Эти граничные условия также могут содержать нелинейные операторы.
 и
и  на границе
на границе  соответствует пространство Соболева
соответствует пространство Соболева  . Эта задача при любой функции f из сопряженного пространства
. Эта задача при любой функции f из сопряженного пространства 
 ,
,  , имеет единственное решение и из
, имеет единственное решение и из  . Здесь и ниже
. Здесь и ниже  есть замыкание множества всех бесконечнодифференцируемых финитных в
есть замыкание множества всех бесконечнодифференцируемых финитных в  функций в пространстве Соболева
функций в пространстве Соболева  .
.
 и краевые задачи.
и краевые задачи.

 . При этом коэффициенты уравнений удовлетворяют определенным условиям.
. При этом коэффициенты уравнений удовлетворяют определенным условиям.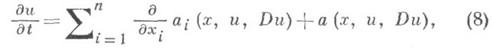

 для определенных классов нелинейных уравнений (6) - (9) основано либо на максимума принципе, либо на специальных интегральных неравенствах и соответствующих вложения теоремах функциональных пространств. Теория разрешимости в целом краевых задач для существенно нелинейных скалярных уравнений эллиптич. типа развита для узкого класса таких уравнений в случае двух независимых переменных.
для определенных классов нелинейных уравнений (6) - (9) основано либо на максимума принципе, либо на специальных интегральных неравенствах и соответствующих вложения теоремах функциональных пространств. Теория разрешимости в целом краевых задач для существенно нелинейных скалярных уравнений эллиптич. типа развита для узкого класса таких уравнений в случае двух независимых переменных.
 .
.
 и такой, что выполнено условие Бернштейна
и такой, что выполнено условие Бернштейна
 с возрастающей функцией
с возрастающей функцией  . Тогда если существуют функции
. Тогда если существуют функции  с
с  такие, что
такие, что  почти всюду в
почти всюду в  на
на  ,
,  почти всюду в
почти всюду в  на
на  (u + - верхнее решение задачи (10),
(u + - верхнее решение задачи (10),  - нижнее решение задачи (10)), и
- нижнее решение задачи (10)), и  в
в  , то существует решение
, то существует решение  задачи (10) и
задачи (10) и  в
в  . Правильный выбор верхних и нижних решений исходных нелинейных задач, основанный на решениях модельных задач, дает возможность устанавливать не только разрешимость и нижнее число решений, но и получать тонкие априорные оценки и асимптотику для этих решений исходных нелинейных задач.
. Правильный выбор верхних и нижних решений исходных нелинейных задач, основанный на решениях модельных задач, дает возможность устанавливать не только разрешимость и нижнее число решений, но и получать тонкие априорные оценки и асимптотику для этих решений исходных нелинейных задач. ,
,  ) разрешимость задачи Коши в целом установлена для отдельных уравнений вида
) разрешимость задачи Коши в целом установлена для отдельных уравнений вида

 и
и  при
при  в определенном классе бесконечно гладких по хфункций. Здесь
в определенном классе бесконечно гладких по хфункций. Здесь  - ограниченная область из
- ограниченная область из  с границей
с границей  класса
класса  и
и 


 . Сложность этого вопроса обусловлена бесконечномерностью ядра соответствующей линейной задачи. Слабо нелинейные и квазилинейные гиперболич. уравнения, содержащие диссипативные слагаемые, исследованы более полно. Нелинейные уравнения с частными производными высшего порядка. Разрешимость краевых (смешанных) задач исследована для широкого класса квазилинейных уравнений дивергентного вида
. Сложность этого вопроса обусловлена бесконечномерностью ядра соответствующей линейной задачи. Слабо нелинейные и квазилинейные гиперболич. уравнения, содержащие диссипативные слагаемые, исследованы более полно. Нелинейные уравнения с частными производными высшего порядка. Разрешимость краевых (смешанных) задач исследована для широкого класса квазилинейных уравнений дивергентного вида
 предполагается выполненным ряд условий, к-рые обеспечивают, что нелинейные операторы будут определены в соответствующих функциональных пространствах и обладать рядом свойств. Напр., для разрешимости краевой задачи в ограниченной области
предполагается выполненным ряд условий, к-рые обеспечивают, что нелинейные операторы будут определены в соответствующих функциональных пространствах и обладать рядом свойств. Напр., для разрешимости краевой задачи в ограниченной области  с условиями
с условиями
 являются измеримыми по хпри всех
являются измеримыми по хпри всех  , непрерывными по
, непрерывными по  почти при всех
почти при всех  и удовлетворяют неравенству
и удовлетворяют неравенству
 и
и  ,
, 
 из пространства Соболева
из пространства Соболева  справедливо неравенство
справедливо неравенство
 и
и  из
из  справедливо неравенство
справедливо неравенство
 имеет решение
имеет решение из
из 



 . С помощью этого метода удалось рассмотреть отдельные нелинейные уравнения типа уравнения Кортевега - де Фриса с двумя пространственными переменными.
. С помощью этого метода удалось рассмотреть отдельные нелинейные уравнения типа уравнения Кортевега - де Фриса с двумя пространственными переменными.