|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НЕКРАСОВА ИНТЕГРАЛЬНОЕ УРАВНЕНИЕЗначение НЕКРАСОВА ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ в математической энциклопедии: - нелинейное интегральное уравнение вида
где R, К- известные функции, причем К- симметричная функция, Иногда уравнения типа (*) наз. Гаммерштейна уравнением, хотя А. И. Некрасов [2] свои исследования опубликовал раньше А. Гаммерштейна [3]. Лит.:[1] Некрасов А. И., Собр. соч., т. 1, М., 1961; [2] его же, "Изв. Иваново-Возн. политехи, ин-та", 1922, № 6, с. 155-71; [3] Нammеrstein A., "Acta math." 1930 Bd 54, S. 117 - 76. Б. В. Хведелидзе. |
|
|
|
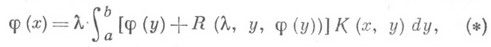
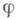- искомая функция,
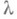- числовой параметр. Интегральные уравнения такого типа были получены А. И. Некрасовым (см. [1]) при решении задач, возникающих в теории волн на поверхности жидкости. А. И. Некрасов в определенных условиях строит решение уравнения (*) в виде ряда по степеням малого параметра, сходимость к-рого доказывается методом мажорант.