Математический словарь
|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НЕЙМАНА ФУНКЦИИЗначение НЕЙМАНА ФУНКЦИИ в математической энциклопедии: - цилиндрические функции2-го рода. Н. ф.
Н. ф. действительны при действительном положительном хи стремятся к нулю при
Н. ф. связаны рекуррентными формулами
При р=п целых:
для малых х:
где
Н. ф. для "полуцелого" порядка
Н. ф. предложены К. Нейманом (К. Neumann, 1867). Лит. см. при ст. Цилиндрические функции. В. И. Битюцков. |
|
|
|

 [иногда применяется обозначение
[иногда применяется обозначение  ] могут быть определены через Бесселя функ ции
] могут быть определены через Бесселя функ ции следующим образом:
следующим образом:
 . При больших хсправедливо асимптотич. представление
. При больших хсправедливо асимптотич. представление
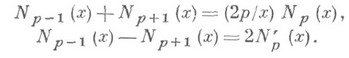


 - постоянная Эйлера.
- постоянная Эйлера.
 выражаются через тригонометрич. функции, в частности
выражаются через тригонометрич. функции, в частности