"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НЕЙМАНА МЕТОД ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ
Значение НЕЙМАНА МЕТОД ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ в математической энциклопедии:
- один из методов доверительного оценивания, позволяющий получать интервальные оценки для неизвестных параметров вероятностных законов по результатам наблюдений. Предложен и развит Ю. Нейманом (см. [1], [2]). Суть метода заключается в следующем. Пусть  - случайные величины, совместная функция распределения к-рых
- случайные величины, совместная функция распределения к-рых  зависит от параметра
зависит от параметра  Далее, пусть в качестве точечной оценки параметра
Далее, пусть в качестве точечной оценки параметра  используется статистика
используется статистика  функция распределения к-рой есть
функция распределения к-рой есть  Тогда для любого числа Риз интервала
Тогда для любого числа Риз интервала  можно определить систему из двух уравнений относительно переменной
можно определить систему из двух уравнений относительно переменной  :
:

При определенных условиях регулярности функции  к-рые выполняются почти во всех интересных для практики случаях, система
к-рые выполняются почти во всех интересных для практики случаях, система  имеет единственное решение
имеет единственное решение

такое, что

Множество  наз. доверительным интервалом (доверительной оценкой) для неизвестного параметра
наз. доверительным интервалом (доверительной оценкой) для неизвестного параметра  с доверительной вероятностью
с доверительной вероятностью  . Статистики
. Статистики  наз. нижним и верхним доверительными пределами, отвечающими выбранному коэффициенту доверия Р. В свою очередь, число
наз. нижним и верхним доверительными пределами, отвечающими выбранному коэффициенту доверия Р. В свою очередь, число

наз. коэффициентом доверия доверительного интервала  . Таким образом, Н. м. д. и. приводит к интервальным оценкам, коэффициент доверия к-рых
. Таким образом, Н. м. д. и. приводит к интервальным оценкам, коэффициент доверия к-рых 
Пример 1. Пусть независимые случайные величины  подчиняются одному и тому же нормальному закону
подчиняются одному и тому же нормальному закону  математич. ожидание к-рого
математич. ожидание к-рого  неизвестно. В этом случае наилучшей оценкой для
неизвестно. В этом случае наилучшей оценкой для  является достаточная статистика
является достаточная статистика  к-рая распределена по нормальному закону
к-рая распределена по нормальному закону  . Фиксируя Риз интервала
. Фиксируя Риз интервала  и решая уравнения
и решая уравнения

находят нижний и верхний доверительные пределы

отвечающие выбранному коэффициенту доверия Р. Так как

то доверительный интервал для неизвестного математич. ожидания G нормального закона  имеет вид
имеет вид

причем коэффициент доверия его в точности равен 2P-1.
Пример 2. Пусть  - случайная величина, подчиняющаяся биномиальному закону с параметрами nи
- случайная величина, подчиняющаяся биномиальному закону с параметрами nи  , т. е. для любого целого
, т. е. для любого целого 

где 
- неполная бета-функция  . Если параметр "успеха"
. Если параметр "успеха"  неизвестен, то для определения доверительных пределов нужно согласно Н. м. д. и. решить уравнения
неизвестен, то для определения доверительных пределов нужно согласно Н. м. д. и. решить уравнения

где  . По таблицам математич. статистики определяют корни
. По таблицам математич. статистики определяют корни  и
и  этих уравнений, являющиеся соответственно верхним и нижним доверительными пределами с коэффициентом доверия Р. Полученный таким образом доверительный интервал
этих уравнений, являющиеся соответственно верхним и нижним доверительными пределами с коэффициентом доверия Р. Полученный таким образом доверительный интервал 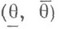 имеет коэффициент, в точности равный
имеет коэффициент, в точности равный  . Очевидно, что если в эксперименте получают
. Очевидно, что если в эксперименте получают  то в этом случае
то в этом случае  если же
если же 
Н. м. д. и. существенно отличается от бейесовского метода и метода, основанного на фидуциальном подходе Фишера. В Н. м. д. и. неизвестный параметр  функции распределения
функции распределения  трактуется как постоянная величина, а сам доверительный интервал
трактуется как постоянная величина, а сам доверительный интервал 
 строится до эксперимента, в ходе к-рого вычисляется значение статистики Т. Следовательно, согласно Н. м. д. и. вероятность одновременного выполнения неравенств
строится до эксперимента, в ходе к-рого вычисляется значение статистики Т. Следовательно, согласно Н. м. д. и. вероятность одновременного выполнения неравенств  есть априорная вероятность того, что доверительный интервал
есть априорная вероятность того, что доверительный интервал  "накрывает" неизвестное истинное значение параметра
"накрывает" неизвестное истинное значение параметра  . Очевидно, что на самом деле доверительный метод Неймана остается в силе, если
. Очевидно, что на самом деле доверительный метод Неймана остается в силе, если  является случайной величиной, так как в Н. м. д. и. интервальная оценка строится до проведения эксперимента и, следовательно, не зависит от априорного распределения параметра. Н. м. д. и. выгодно отличается от бейесовского и фидуциального подходов своей независимостью от априорной информации о параметре
является случайной величиной, так как в Н. м. д. и. интервальная оценка строится до проведения эксперимента и, следовательно, не зависит от априорного распределения параметра. Н. м. д. и. выгодно отличается от бейесовского и фидуциального подходов своей независимостью от априорной информации о параметре  , и при этом, в отличие от метода Фишера, логически безупречен. В общем случае Н. м. д. и. приводит к целой системе доверительных интервалов для неизвестного параметра, в связи с чем возникает задача построения оптимальной интервальной оценки, обладающей, напр., свойствами несмещенности, селективности или подобия, к-рая находит свое решение в рамках теории проверки статистич. гипотез.
, и при этом, в отличие от метода Фишера, логически безупречен. В общем случае Н. м. д. и. приводит к целой системе доверительных интервалов для неизвестного параметра, в связи с чем возникает задача построения оптимальной интервальной оценки, обладающей, напр., свойствами несмещенности, селективности или подобия, к-рая находит свое решение в рамках теории проверки статистич. гипотез.
Лит.:[1] Neyman J., "Ann. Math. Statistics", 1935, v. 6, p. 111 -16; [2] eго же, "Philos. Trans. Roy. Soc. London. Ser. A.", 1937, v. 236, p. 333-80; [3] Большев Л. Н., Смирнов Н. В., Таблицы математической статистики, 2 изд., М., 1968; [4] Большев Л. Н., "Теория вероятн. и ее примен.", 1965, т. 10, № 1, с. 187-92; [5] Леман Э., Проверка статистических гипотез, пер. с англ., 2 изд., М., 1979.
М. С. Никулин.

 - случайные величины, совместная функция распределения к-рых
- случайные величины, совместная функция распределения к-рых  зависит от параметра
зависит от параметра  Далее, пусть в качестве точечной оценки параметра
Далее, пусть в качестве точечной оценки параметра  используется статистика
используется статистика  функция распределения к-рой есть
функция распределения к-рой есть  Тогда для любого числа Риз интервала
Тогда для любого числа Риз интервала  можно определить систему из двух уравнений относительно переменной
можно определить систему из двух уравнений относительно переменной  :
:
 к-рые выполняются почти во всех интересных для практики случаях, система
к-рые выполняются почти во всех интересных для практики случаях, система  имеет единственное решение
имеет единственное решение

 наз. доверительным интервалом (доверительной оценкой) для неизвестного параметра
наз. доверительным интервалом (доверительной оценкой) для неизвестного параметра  с доверительной вероятностью
с доверительной вероятностью  . Статистики
. Статистики  наз. нижним и верхним доверительными пределами, отвечающими выбранному коэффициенту доверия Р. В свою очередь, число
наз. нижним и верхним доверительными пределами, отвечающими выбранному коэффициенту доверия Р. В свою очередь, число
 . Таким образом, Н. м. д. и. приводит к интервальным оценкам, коэффициент доверия к-рых
. Таким образом, Н. м. д. и. приводит к интервальным оценкам, коэффициент доверия к-рых 
 подчиняются одному и тому же нормальному закону
подчиняются одному и тому же нормальному закону  математич. ожидание к-рого
математич. ожидание к-рого  неизвестно. В этом случае наилучшей оценкой для
неизвестно. В этом случае наилучшей оценкой для  является достаточная статистика
является достаточная статистика  к-рая распределена по нормальному закону
к-рая распределена по нормальному закону  . Фиксируя Риз интервала
. Фиксируя Риз интервала  и решая уравнения
и решая уравнения


 имеет вид
имеет вид
 - случайная величина, подчиняющаяся биномиальному закону с параметрами nи
- случайная величина, подчиняющаяся биномиальному закону с параметрами nи  , т. е. для любого целого
, т. е. для любого целого 


 . Если параметр "успеха"
. Если параметр "успеха"  неизвестен, то для определения доверительных пределов нужно согласно Н. м. д. и. решить уравнения
неизвестен, то для определения доверительных пределов нужно согласно Н. м. д. и. решить уравнения
 . По таблицам математич. статистики определяют корни
. По таблицам математич. статистики определяют корни  и
и  этих уравнений, являющиеся соответственно верхним и нижним доверительными пределами с коэффициентом доверия Р. Полученный таким образом доверительный интервал
этих уравнений, являющиеся соответственно верхним и нижним доверительными пределами с коэффициентом доверия Р. Полученный таким образом доверительный интервал 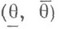 имеет коэффициент, в точности равный
имеет коэффициент, в точности равный  . Очевидно, что если в эксперименте получают
. Очевидно, что если в эксперименте получают  то в этом случае
то в этом случае  если же
если же 
 функции распределения
функции распределения  трактуется как постоянная величина, а сам доверительный интервал
трактуется как постоянная величина, а сам доверительный интервал 
 строится до эксперимента, в ходе к-рого вычисляется значение статистики Т. Следовательно, согласно Н. м. д. и. вероятность одновременного выполнения неравенств
строится до эксперимента, в ходе к-рого вычисляется значение статистики Т. Следовательно, согласно Н. м. д. и. вероятность одновременного выполнения неравенств  есть априорная вероятность того, что доверительный интервал
есть априорная вероятность того, что доверительный интервал  "накрывает" неизвестное истинное значение параметра
"накрывает" неизвестное истинное значение параметра  . Очевидно, что на самом деле доверительный метод Неймана остается в силе, если
. Очевидно, что на самом деле доверительный метод Неймана остается в силе, если  является случайной величиной, так как в Н. м. д. и. интервальная оценка строится до проведения эксперимента и, следовательно, не зависит от априорного распределения параметра. Н. м. д. и. выгодно отличается от бейесовского и фидуциального подходов своей независимостью от априорной информации о параметре
является случайной величиной, так как в Н. м. д. и. интервальная оценка строится до проведения эксперимента и, следовательно, не зависит от априорного распределения параметра. Н. м. д. и. выгодно отличается от бейесовского и фидуциального подходов своей независимостью от априорной информации о параметре  , и при этом, в отличие от метода Фишера, логически безупречен. В общем случае Н. м. д. и. приводит к целой системе доверительных интервалов для неизвестного параметра, в связи с чем возникает задача построения оптимальной интервальной оценки, обладающей, напр., свойствами несмещенности, селективности или подобия, к-рая находит свое решение в рамках теории проверки статистич. гипотез.
, и при этом, в отличие от метода Фишера, логически безупречен. В общем случае Н. м. д. и. приводит к целой системе доверительных интервалов для неизвестного параметра, в связи с чем возникает задача построения оптимальной интервальной оценки, обладающей, напр., свойствами несмещенности, селективности или подобия, к-рая находит свое решение в рамках теории проверки статистич. гипотез.