"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НЕАТОМИЧЕСКАЯ ИГРА
Значение НЕАТОМИЧЕСКАЯ ИГРА в математической энциклопедии:
- игра, в к-рой на множестве всех игроков I задана s-алгебра подмножеств и на  существует такая неатомическая мера, что множества игроков
существует такая неатомическая мера, что множества игроков  , имеющие нулевую меру, не оказывают влияния на исход игры. Н. и. служат моделями ситуаций, в к-рых имеются большие количества очень "малых" индивидуумов, подобных потребителям в экономич. системе, и развитие теории Н. и. было тесно связано с изучением моделей, экономик с большим числом участников (см. [1]). Н. и. подчиняются общей классификации, принятой в игр теории, и основные теоретико-игровые принципы оптимальности (см. Ядро в теории игр, Шепли вектор )естественным образом на них распространяются. При этом стратегич. принципы оптимальности в Н. и. реализуются, как правило, без обычных предположений о выпуклости (см. [2]), и различные принципы оптимальности в Н. и. оказываются более тесно связанными между собой; напр., для широкого класса неатомич. моделей типа рынков множество конкурентных равновесий совпадает с с-ядром, к-рое состоит из единственного элемента, совпадающего со значением игры (аналогом вектора Шепли для Н. и., см. [1]). Разрабатываются два направления - кооперативная теория Н. и. (см. [1], [3], [4]) и теория бескоалиционных Н. и. (см. [2]).
, имеющие нулевую меру, не оказывают влияния на исход игры. Н. и. служат моделями ситуаций, в к-рых имеются большие количества очень "малых" индивидуумов, подобных потребителям в экономич. системе, и развитие теории Н. и. было тесно связано с изучением моделей, экономик с большим числом участников (см. [1]). Н. и. подчиняются общей классификации, принятой в игр теории, и основные теоретико-игровые принципы оптимальности (см. Ядро в теории игр, Шепли вектор )естественным образом на них распространяются. При этом стратегич. принципы оптимальности в Н. и. реализуются, как правило, без обычных предположений о выпуклости (см. [2]), и различные принципы оптимальности в Н. и. оказываются более тесно связанными между собой; напр., для широкого класса неатомич. моделей типа рынков множество конкурентных равновесий совпадает с с-ядром, к-рое состоит из единственного элемента, совпадающего со значением игры (аналогом вектора Шепли для Н. и., см. [1]). Разрабатываются два направления - кооперативная теория Н. и. (см. [1], [3], [4]) и теория бескоалиционных Н. и. (см. [2]).
Кооперативная неатомическая и г-р а, по аналогии с обычной кооперативной игрой, задается в виде тройки 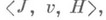 где
где 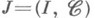 - измеримое пространство игроков, элементы
- измеримое пространство игроков, элементы  наз. коалициями, v- действительнозначная функция на
наз. коалициями, v- действительнозначная функция на  , наз. характеристической функцией, а H - нек-рое подмножество множества
, наз. характеристической функцией, а H - нек-рое подмножество множества 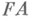 всех конечно аддитивных мер ограниченной вариации на
всех конечно аддитивных мер ограниченной вариации на  {обычно предполагается, что
{обычно предполагается, что  для всех
для всех  ).
).
В простейшем случае vявляется функцией от неатомич. меры на 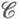 . Предполагается, что пространство J стандартно, а функция множества vимеет ограниченную вариацию (т. е. представима в виде разности двух монотонных функций). Описаны [1] различные подпространства пространства BV всех функций ограниченной вариации на
. Предполагается, что пространство J стандартно, а функция множества vимеет ограниченную вариацию (т. е. представима в виде разности двух монотонных функций). Описаны [1] различные подпространства пространства BV всех функций ограниченной вариации на  , для к-рых можно построить аналог вектора Шепли (как положительный линейный оператор со значениями в FA).
, для к-рых можно построить аналог вектора Шепли (как положительный линейный оператор со значениями в FA).
Понятия сбалансированной игры, игры рынка, игры без побочных платежей (см. Кооперативная игра )и "вязанные с ними результаты переносятся на кооперативные Н. и. (см. [3], [4]).
Определение бескоалиционной неатомической игры аналогично определению жлассич. понятия бескоалиционной игры. Для бескоалиционных Н. и. известны аналог Нэша теоремы, а также общие результаты о существовании ситуаций равновесия без предположений о выпуклости, к-рые не имеют места для игр с конечным числом участников (см. [2]).
Лит.:[1] Ауман Р., Щепли Л., Значения для неатомических игр, пер. с англ., М., 1977; [2] Кирута А. Я., в кн.: Математические методы в социальных науках, в. 6, Вильнюс, 1975, с. 18-71; [3] Розенмюллер И., Кооперативные игры и рынки, пер. с нем., М., 1974; [4] Rоsenmullеr J., "Operat. Res. Verfahren", 1975, Bd 20, S. 107-28.
А. Я. Кирута, Е. Б. Яновская.

 существует такая
существует такая  , имеющие нулевую меру, не оказывают влияния на исход игры. Н. и. служат моделями ситуаций, в к-рых имеются большие количества очень "малых" индивидуумов, подобных потребителям в экономич. системе, и развитие теории Н. и. было тесно связано с изучением моделей, экономик с большим числом участников (см. [1]). Н. и. подчиняются общей классификации, принятой в игр теории, и основные теоретико-игровые принципы оптимальности (см. Ядро в теории игр, Шепли вектор )естественным образом на них распространяются. При этом стратегич. принципы оптимальности в Н. и. реализуются, как правило, без обычных предположений о выпуклости (см. [2]), и различные принципы оптимальности в Н. и. оказываются более тесно связанными между собой; напр., для широкого класса неатомич. моделей типа рынков множество конкурентных равновесий совпадает с с-ядром, к-рое состоит из единственного элемента, совпадающего со значением игры (аналогом вектора Шепли для Н. и., см. [1]). Разрабатываются два направления - кооперативная теория Н. и. (см. [1], [3], [4]) и теория бескоалиционных Н. и. (см. [2]).
, имеющие нулевую меру, не оказывают влияния на исход игры. Н. и. служат моделями ситуаций, в к-рых имеются большие количества очень "малых" индивидуумов, подобных потребителям в экономич. системе, и развитие теории Н. и. было тесно связано с изучением моделей, экономик с большим числом участников (см. [1]). Н. и. подчиняются общей классификации, принятой в игр теории, и основные теоретико-игровые принципы оптимальности (см. Ядро в теории игр, Шепли вектор )естественным образом на них распространяются. При этом стратегич. принципы оптимальности в Н. и. реализуются, как правило, без обычных предположений о выпуклости (см. [2]), и различные принципы оптимальности в Н. и. оказываются более тесно связанными между собой; напр., для широкого класса неатомич. моделей типа рынков множество конкурентных равновесий совпадает с с-ядром, к-рое состоит из единственного элемента, совпадающего со значением игры (аналогом вектора Шепли для Н. и., см. [1]). Разрабатываются два направления - кооперативная теория Н. и. (см. [1], [3], [4]) и теория бескоалиционных Н. и. (см. [2]).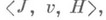 где
где 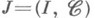 - измеримое пространство игроков, элементы
- измеримое пространство игроков, элементы  наз. коалициями, v- действительнозначная функция на
наз. коалициями, v- действительнозначная функция на  , наз. характеристической функцией, а H - нек-рое подмножество множества
, наз. характеристической функцией, а H - нек-рое подмножество множества 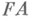 всех конечно аддитивных мер ограниченной вариации на
всех конечно аддитивных мер ограниченной вариации на  {обычно предполагается, что
{обычно предполагается, что  для всех
для всех  ).
).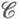 . Предполагается, что пространство J стандартно, а функция множества vимеет ограниченную вариацию (т. е. представима в виде разности двух монотонных функций). Описаны [1] различные подпространства пространства BV всех функций ограниченной вариации на
. Предполагается, что пространство J стандартно, а функция множества vимеет ограниченную вариацию (т. е. представима в виде разности двух монотонных функций). Описаны [1] различные подпространства пространства BV всех функций ограниченной вариации на  , для к-рых можно построить аналог вектора Шепли (как положительный линейный оператор со значениями в FA).
, для к-рых можно построить аналог вектора Шепли (как положительный линейный оператор со значениями в FA).