"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НАКРЫТИЕ
Значение НАКРЫТИЕ в математической энциклопедии:
- отображение 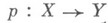 пространства Xна пространство У, при к-ром прообраз нек-рой окрестности U(у)каждой точки
пространства Xна пространство У, при к-ром прообраз нек-рой окрестности U(у)каждой точки 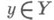 распадается на открытые подмножества, гомеоморфно отображающиеся посредством рна U(у). Эквивалентно: р- локально тривиальное расслоение с дискретным слоем.
распадается на открытые подмножества, гомеоморфно отображающиеся посредством рна U(у). Эквивалентно: р- локально тривиальное расслоение с дискретным слоем.
Обычно Н. рассматривается в предположении связности Xи Y и также локальной связности и локальной односвязности Y. При этих предположениях устанавливается связь между фундаментальными группами 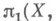
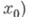 и
и 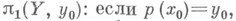 то индуцированный гомоморфизм р * отображает
то индуцированный гомоморфизм р * отображает 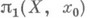 изоморфно на подгруппу в
изоморфно на подгруппу в 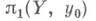 и, меняя точку
и, меняя точку 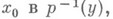 можно получить в точности все подгруппы из нек-рого класса сопряженных подгрупп. Если этот класс состоит из одной подгруппы Н(т. е. Н - нормальный делитель), то Н. наз. регулярным. В этом случае возникает свободное действие группы
можно получить в точности все подгруппы из нек-рого класса сопряженных подгрупп. Если этот класс состоит из одной подгруппы Н(т. е. Н - нормальный делитель), то Н. наз. регулярным. В этом случае возникает свободное действие группы 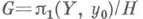 на X, причем роказывается факторотображением на пространство орбит Y. Это действие порождается поднятием петель: если петле
на X, причем роказывается факторотображением на пространство орбит Y. Это действие порождается поднятием петель: если петле 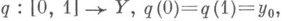 сопоставить единственный путь
сопоставить единственный путь 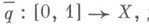 для к-рого
для к-рого 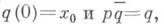 то точка
то точка 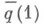 будет зависеть только от класса этой петли в Gи от точки х 0 . Таким образом, элементу из G отвечает перестановка точек в
будет зависеть только от класса этой петли в Gи от точки х 0 . Таким образом, элементу из G отвечает перестановка точек в 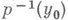 . Эта перестановка не имеет неподвижных точек, если
. Эта перестановка не имеет неподвижных точек, если 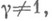 и непрерывно зависит от точки у 0 . Возникает гомеоморфизм X.
и непрерывно зависит от точки у 0 . Возникает гомеоморфизм X.
В общем случае эта конструкция определяет лишь перестановку в 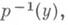 т. е. имеется действие
т. е. имеется действие 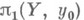 на
на 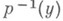 , наз. монодромией накрытия.
, наз. монодромией накрытия.
Частным случаем регулярного Н. является универсальное накрытие, для к-рого 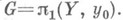 Вообще, по каждой группе
Вообще, по каждой группе 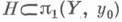 однозначно строится Н. р: X,
однозначно строится Н. р: X, 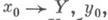 для к-рого
для к-рого 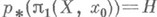 .В качестве точек Xберутся классы путей
.В качестве точек Xберутся классы путей 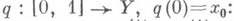 два пути q1 и q2 отождествляются, если q1(l) = q2(l) и петля
два пути q1 и q2 отождествляются, если q1(l) = q2(l) и петля 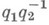 лежит в элементе из Н. Точка q(1)для путей из одного класса считается образом этого класса, что определяет р. Топология в X однозначно задается требованием, чтобы роказалось Н.: при этом существенна локальная односвязность Y. Для любого отображения f линейно связного пространства Z, z0 в Y, у 0 поднятие его до отображения
лежит в элементе из Н. Точка q(1)для путей из одного класса считается образом этого класса, что определяет р. Топология в X однозначно задается требованием, чтобы роказалось Н.: при этом существенна локальная односвязность Y. Для любого отображения f линейно связного пространства Z, z0 в Y, у 0 поднятие его до отображения 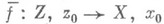 существует тогда и только тогда, когда
существует тогда и только тогда, когда 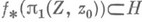 . Между накрытиями Y имеется отношение частичного порядка (накрытие накрытия есть накрытие), двойственное включению подгрупп в
. Между накрытиями Y имеется отношение частичного порядка (накрытие накрытия есть накрытие), двойственное включению подгрупп в 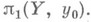 В частности, универсальное Н. является единственным максимальным элементом.
В частности, универсальное Н. является единственным максимальным элементом.
Примеры. Параметризация окружности (cos j, sin j) задает ее Н. числовой прямой 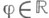 , к-рое часто записывают в комплексной форме е ij и наз. экспоненциальным. Аналогично, тор накрывается плоскостью. При отождествлении диаметрально противоположных точек сферы возникает Н. сферой проективного пространства соответствующей размерности. Вообще, свободные действия дискретных групп - обычный источник регулярных Н. (над пространством орбит, хотя и не всякое такое действие задает Н. (пространство орбит может оказаться неотделимым)), но это так для конечных групп.
, к-рое часто записывают в комплексной форме е ij и наз. экспоненциальным. Аналогично, тор накрывается плоскостью. При отождествлении диаметрально противоположных точек сферы возникает Н. сферой проективного пространства соответствующей размерности. Вообще, свободные действия дискретных групп - обычный источник регулярных Н. (над пространством орбит, хотя и не всякое такое действие задает Н. (пространство орбит может оказаться неотделимым)), но это так для конечных групп.
А. В. Чернявский.

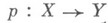 пространства Xна пространство У, при к-ром прообраз нек-рой окрестности U(у)каждой точки
пространства Xна пространство У, при к-ром прообраз нек-рой окрестности U(у)каждой точки 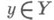 распадается на открытые подмножества, гомеоморфно отображающиеся посредством рна U(у). Эквивалентно: р- локально тривиальное расслоение с дискретным слоем.
распадается на открытые подмножества, гомеоморфно отображающиеся посредством рна U(у). Эквивалентно: р- локально тривиальное расслоение с дискретным слоем.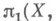
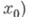 и
и 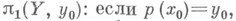 то индуцированный гомоморфизм р * отображает
то индуцированный гомоморфизм р * отображает 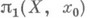 изоморфно на подгруппу в
изоморфно на подгруппу в 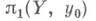 и, меняя точку
и, меняя точку 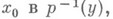 можно получить в точности все подгруппы из нек-рого класса сопряженных подгрупп. Если этот класс состоит из одной подгруппы Н(т. е. Н - нормальный делитель), то Н. наз. регулярным. В этом случае возникает свободное действие группы
можно получить в точности все подгруппы из нек-рого класса сопряженных подгрупп. Если этот класс состоит из одной подгруппы Н(т. е. Н - нормальный делитель), то Н. наз. регулярным. В этом случае возникает свободное действие группы 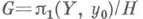 на X, причем роказывается факторотображением на пространство орбит Y. Это действие порождается поднятием петель: если петле
на X, причем роказывается факторотображением на пространство орбит Y. Это действие порождается поднятием петель: если петле 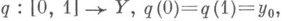 сопоставить единственный путь
сопоставить единственный путь 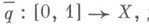 для к-рого
для к-рого 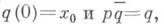 то точка
то точка 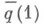 будет зависеть только от класса этой петли в Gи от точки х 0 . Таким образом, элементу из G отвечает перестановка точек в
будет зависеть только от класса этой петли в Gи от точки х 0 . Таким образом, элементу из G отвечает перестановка точек в 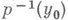 . Эта перестановка не имеет неподвижных точек, если
. Эта перестановка не имеет неподвижных точек, если 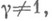 и непрерывно зависит от точки у 0 . Возникает гомеоморфизм X.
и непрерывно зависит от точки у 0 . Возникает гомеоморфизм X.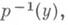 т. е. имеется действие
т. е. имеется действие 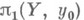 на
на 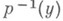 , наз. монодромией накрытия.
, наз. монодромией накрытия.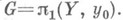 Вообще, по каждой группе
Вообще, по каждой группе 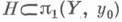 однозначно строится Н. р: X,
однозначно строится Н. р: X, 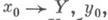 для к-рого
для к-рого 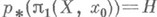 .В качестве точек Xберутся классы путей
.В качестве точек Xберутся классы путей 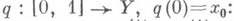 два пути q1 и q2 отождествляются, если q1(l) = q2(l) и петля
два пути q1 и q2 отождествляются, если q1(l) = q2(l) и петля 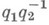 лежит в элементе из Н. Точка q(1)для путей из одного класса считается образом этого класса, что определяет р. Топология в X однозначно задается требованием, чтобы роказалось Н.: при этом существенна локальная односвязность Y. Для любого отображения f линейно связного пространства Z, z0 в Y, у 0 поднятие его до отображения
лежит в элементе из Н. Точка q(1)для путей из одного класса считается образом этого класса, что определяет р. Топология в X однозначно задается требованием, чтобы роказалось Н.: при этом существенна локальная односвязность Y. Для любого отображения f линейно связного пространства Z, z0 в Y, у 0 поднятие его до отображения 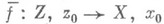 существует тогда и только тогда, когда
существует тогда и только тогда, когда 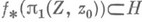 . Между накрытиями Y имеется отношение частичного порядка (накрытие накрытия есть накрытие), двойственное включению подгрупп в
. Между накрытиями Y имеется отношение частичного порядка (накрытие накрытия есть накрытие), двойственное включению подгрупп в 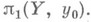 В частности, универсальное Н. является единственным максимальным элементом.
В частности, универсальное Н. является единственным максимальным элементом.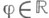 , к-рое часто записывают в комплексной форме е ij и наз. экспоненциальным. Аналогично, тор накрывается плоскостью. При отождествлении диаметрально противоположных точек сферы возникает Н. сферой проективного пространства соответствующей размерности. Вообще, свободные действия дискретных групп - обычный источник регулярных Н. (над пространством орбит, хотя и не всякое такое действие задает Н. (пространство орбит может оказаться неотделимым)), но это так для конечных групп.
, к-рое часто записывают в комплексной форме е ij и наз. экспоненциальным. Аналогично, тор накрывается плоскостью. При отождествлении диаметрально противоположных точек сферы возникает Н. сферой проективного пространства соответствующей размерности. Вообще, свободные действия дискретных групп - обычный источник регулярных Н. (над пространством орбит, хотя и не всякое такое действие задает Н. (пространство орбит может оказаться неотделимым)), но это так для конечных групп.