"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НАИМЕНЬШИХ КВАДРАТОВ МЕТОД
Значение НАИМЕНЬШИХ КВАДРАТОВ МЕТОД в математической энциклопедии:
- один из методов ошибок теории для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки. Н. к. м. применяется также для приближенного представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений. Н. к. м. предложен К. Гауссом (С. Gauss, 1794-95) и А. Лежандром (A. Legendre, 1805-06). Строгое обоснование и установление границ содержательной применимости Н. к. м. даны А. А. Марковым и А. Н. Колмогоровым. В простейшем случае линейных связей (см. ниже) и наблюдений, не содержащих систематич. ошибок, а подверженных лишь случайным ошибкам, оценки неизвестных величин, полученные с помощью Н. к. м., являются линейными функциями от наблюденных значений. Эти оценки не имеют систематич. ошибок, т. е. являются несмещенными (см. Несмещенная оценка). Если случайные ошибки наблюдений независимы и подчиняются нормальному распределению, то Н. к. м. дает оценки неизвестных с наименьшей дисперсией, т. е. эти оценки являются эффективными (см. Статистическое оценивание). В этом смысле Н. к. м. является наилучшим среди всех остальных методов, позволяющих находить несмещенные оценки. Однако если распределение случайных ошибок существенно отличается от нормального, то Н. к. м. может и не быть наилучшим.
При обосновании Н. к. м. (по Гауссу) предполагается, что "убыток" от замены точного (неизвестного) значения нек-рой величины  ее приближенным значением X, вычисленным по результатам наблюдений, пропорционален квадрату ошибки
ее приближенным значением X, вычисленным по результатам наблюдений, пропорционален квадрату ошибки  оптимальной оценкой считается такая лишенная систематич. ошибки величина X, для к-рой среднее значение
оптимальной оценкой считается такая лишенная систематич. ошибки величина X, для к-рой среднее значение  "убытка" минимально. Именно это требование и составляет основу Н. к. м. В общем случае отыскание оптимальной в смысле Н. к. м. оценки X - задача весьма сложная, поэтому практически эту задачу сужают и в качестве Xвыбирают линейную функцию от результатов наблюдений, лишенную систематич. ошибки, и такую, для к-рой среднее значение убытка минимально в классе всех линейных функций. Если случайные ошибки наблюдений подчиняются нормальному распределению и оцениваемая величина mзависит от средних значений результатов наблюдений линейно (случай, весьма часто встречающийся в приложениях Н. к. м.), то решение этой задачи будет одновременно являться и решением общей задачи. При этом оптимальная оценка Xтакже подчиняется нормальному распределению со средним значением
"убытка" минимально. Именно это требование и составляет основу Н. к. м. В общем случае отыскание оптимальной в смысле Н. к. м. оценки X - задача весьма сложная, поэтому практически эту задачу сужают и в качестве Xвыбирают линейную функцию от результатов наблюдений, лишенную систематич. ошибки, и такую, для к-рой среднее значение убытка минимально в классе всех линейных функций. Если случайные ошибки наблюдений подчиняются нормальному распределению и оцениваемая величина mзависит от средних значений результатов наблюдений линейно (случай, весьма часто встречающийся в приложениях Н. к. м.), то решение этой задачи будет одновременно являться и решением общей задачи. При этом оптимальная оценка Xтакже подчиняется нормальному распределению со средним значением  и, следовательно, плотность вероятности случайной величины X
и, следовательно, плотность вероятности случайной величины X

достигает максимума в точке  (это свойство и выражает точное содержание распространенного в теории ошибок утверждения: "оценка X, вычисленная согласно Н. к. м.,- наиболее вероятное значение неизвестного параметра
(это свойство и выражает точное содержание распространенного в теории ошибок утверждения: "оценка X, вычисленная согласно Н. к. м.,- наиболее вероятное значение неизвестного параметра  ").
").
Случай одного неизвестного. Пусть для оценки значения неизвестной величины  произведено пнезависимых наблюдений, давших результаты
произведено пнезависимых наблюдений, давших результаты 
 - случайные ошибки (по определению, принятому в классич. теории ошибок, случайные ошибки - независимые случайные величины с нулевым математич. ожиданием:
- случайные ошибки (по определению, принятому в классич. теории ошибок, случайные ошибки - независимые случайные величины с нулевым математич. ожиданием:
 ; если же
; если же  наз. систематическими ошибками). Согласно Н. к. м. в качестве оценки величины m. принимают такое X, для к-рого будет наименьшей сумма квадратов (отсюда и само название метода):
наз. систематическими ошибками). Согласно Н. к. м. в качестве оценки величины m. принимают такое X, для к-рого будет наименьшей сумма квадратов (отсюда и само название метода):

где 
(коэффициент k>0 можно выбирать произвольно). Величину  наз. весом, а
наз. весом, а  -квадратичным отклонением измерения с номером
-квадратичным отклонением измерения с номером  . В частности, если все измерения равноточны, то
. В частности, если все измерения равноточны, то  и в этом случае можно положить
и в этом случае можно положить  если же каждое
если же каждое  - арифметич. среднее из
- арифметич. среднее из  равноточных измерений, то полагают
равноточных измерений, то полагают 
Сумма  будет наименьшей, если в качестве Xвыбрать взвешенное среднее:
будет наименьшей, если в качестве Xвыбрать взвешенное среднее:

Оценка  величины
величины  лишена систематич. ошибки, имеет вес Ри дисперсию
лишена систематич. ошибки, имеет вес Ри дисперсию  . В частности, если все измерения равноточны, то Y - арифметич. среднее результатов измерений:
. В частности, если все измерения равноточны, то Y - арифметич. среднее результатов измерений:

При нек-рых общих предположениях можно показать, что если количество наблюдений пдостаточно велико, то распределение оценки У мало отличается от нормального с математич. ожиданием m и дисперсией  .В этом случае абсолютная погрешность приближенного равенства
.В этом случае абсолютная погрешность приближенного равенства  меньше
меньше  с вероятностью, близкой к значению интеграла
с вероятностью, близкой к значению интеграла

(напр.,  ).
).
Если веса измерений  заданы, а множитель кдо наблюдений остается неопределенным, то этот множитель и дисперсия оценки
заданы, а множитель кдо наблюдений остается неопределенным, то этот множитель и дисперсия оценки  могут быть оценены по формулам:
могут быть оценены по формулам:
и

(обе оценки лишены систематич. ошибок).
В том практически важном случае, когда ошибки  подчиняются нормальному распределению, можно найти точное значение вероятности, с к-рой абсолютная погрешность приближенного равенства
подчиняются нормальному распределению, можно найти точное значение вероятности, с к-рой абсолютная погрешность приближенного равенства  окажется меньше
окажется меньше  (t- произвольное положительное число):
(t- произвольное положительное число):

где постоянная  выбрана таким образом, чтобы выполнялось условие
выбрана таким образом, чтобы выполнялось условие  ( Стьюдента распре деление с п-1 степенями свободы). При больших пформулу (2) можно заменить формулой (1). Однако применение формулы (1) при небольших ппривело бы к грубым ошибкам. Так, напр., согласно (1) значению I= 0,99 соответствует t=2,58; истинные значения t, определяемые при малых пкак решения соответствующих уравнений
( Стьюдента распре деление с п-1 степенями свободы). При больших пформулу (2) можно заменить формулой (1). Однако применение формулы (1) при небольших ппривело бы к грубым ошибкам. Так, напр., согласно (1) значению I= 0,99 соответствует t=2,58; истинные значения t, определяемые при малых пкак решения соответствующих уравнений  приведены в таблице:
приведены в таблице:

Пример. Для определения массы нек-рого тела произведено 10 независимых равноточных взвешиваний, давших результаты Yi (в г):

(здесь ni - число случаев, в к-рых наблюдалась масса  ). Так как все взвешивания равноточные, то следует положить
). Так как все взвешивания равноточные, то следует положить  и в качестве оценки для неизвестного веса
и в качестве оценки для неизвестного веса  выбрать величину
выбрать величину 
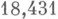 . Задавая, напр.,
. Задавая, напр., по таблицам распределения Стьюдента с девятью степенями свободы можно найти, что
по таблицам распределения Стьюдента с девятью степенями свободы можно найти, что  и поэтому в качестве предельной абсолютной погрешности приближенного равенства
и поэтому в качестве предельной абсолютной погрешности приближенного равенства  следует принять величину
следует принять величину

Таким образом,
Случай нескольких неизвестных (линейные связи). Пусть презультатов измерений  связаны с тнеизвестными величинами
связаны с тнеизвестными величинами  независимыми линейными соотношениями
независимыми линейными соотношениями

где  - известные коэффициенты, а
- известные коэффициенты, а  - независимые случайные ошибки измерений.
- независимые случайные ошибки измерений.
Требуется оценить неизвестные величины  (эту задачу можно рассматривать как обобщение предыдущей, в к-рой
(эту задачу можно рассматривать как обобщение предыдущей, в к-рой

Так как  то средние значения результатов измерений
то средние значения результатов измерений  связаны с неизвестными величинами
связаны с неизвестными величинами  линейными уравнениями (линейные связи):
линейными уравнениями (линейные связи):

Следовательно, искомые величины  представляют собой решение системы (4), уравнения к-рой предполагаются совместными. Точные значения измеряемых величин
представляют собой решение системы (4), уравнения к-рой предполагаются совместными. Точные значения измеряемых величин  и случайные ошибки
и случайные ошибки  обычно неизвестны, поэтому вместо систем (3) и (4) принято записывать так наз. условные уравнения
обычно неизвестны, поэтому вместо систем (3) и (4) принято записывать так наз. условные уравнения

Согласно Н. к. м. в качестве оценок для неизвестных  применяют такие величины
применяют такие величины  , для к-рых сумма квадратов отклонений
, для к-рых сумма квадратов отклонений

будет наименьшей (как и в предыдущем случае, - вес измерения,
- вес измерения, - величина, обратно пропорциональная дисперсии случайной ошибки
- величина, обратно пропорциональная дисперсии случайной ошибки  ). Условные уравнения, как правило, несовместны, т. с. при любых значениях
). Условные уравнения, как правило, несовместны, т. с. при любых значениях  разности
разности

не могут, вообще говоря, все обратиться в нуль. Н. к. м. предписывает в качестве оценок выбрать такие значения  , к-рые минимизируют сумму S. В тех исключительных случаях, когда условные уравнения совместны и, значит, обладают решением, это решение совпадает с оценками, полученными согласно Н. к. м.
, к-рые минимизируют сумму S. В тех исключительных случаях, когда условные уравнения совместны и, значит, обладают решением, это решение совпадает с оценками, полученными согласно Н. к. м.
Сумма квадратов Sпредставляет собой квадратичный многочлен относительно переменных  ; этот многочлен достигает минимума при таких значениях
; этот многочлен достигает минимума при таких значениях 
 при к-рых обращаются в нуль все первые частные производные:
при к-рых обращаются в нуль все первые частные производные:

Отсюда следует, что оценки  , полученные согласно Н. к. м., должны удовлетворять системе т. н. нормальных уравнений, к-рая в обозначениях, предложенных К. Гауссом, имеет вид
, полученные согласно Н. к. м., должны удовлетворять системе т. н. нормальных уравнений, к-рая в обозначениях, предложенных К. Гауссом, имеет вид

где

и

Оценки, получающиеся в результате решения системы нормальных уравнений, лишены систематич. ошибок
 дисперсии
дисперсии  величин
величин  равны
равны 
где d- определитель системы (5), а  - минор, соответствующий диагональному элементу
- минор, соответствующий диагональному элементу  (иными словами,
(иными словами, - вес оценки
- вес оценки  ). Если множитель пропорциональности (кназ. дисперсией на единицу веса) заранее неизвестен, то для его оценки, а также для оценки дисперсии
). Если множитель пропорциональности (кназ. дисперсией на единицу веса) заранее неизвестен, то для его оценки, а также для оценки дисперсии  служат формулы
служат формулы

(S- минимальное значение исходной суммы квадратов). При нек-рых общих предположениях можно показать, что если количество наблюдений пдостаточно велико, то абсолютная погрешность приближенного равенства  меньше
меньше  с вероятностью, близкой к значению интеграла (1). Если случайные ошибки наблюдений
с вероятностью, близкой к значению интеграла (1). Если случайные ошибки наблюдений  подчиняются нормальному распределению, то все отношения
подчиняются нормальному распределению, то все отношения  распределены по закону Стьюдента с п-то степенями свободы (точная оценка абсолютной погрешности приближенного равенства производится здесь с помощью интеграла (2) так же, как в случае одного неизвестного). Кроме того, минимальное значение суммы Sв вероятностном смысле не зависит от
распределены по закону Стьюдента с п-то степенями свободы (точная оценка абсолютной погрешности приближенного равенства производится здесь с помощью интеграла (2) так же, как в случае одного неизвестного). Кроме того, минимальное значение суммы Sв вероятностном смысле не зависит от  и потому приближенные значения дисперсий оценок
и потому приближенные значения дисперсий оценок  не зависят от самих оценок
не зависят от самих оценок 
Один из наиболее типичных случаев применения Н. к. м.- "выравнивание" таких результатов наблюдений  , для к-рых в уравнениях (3)
, для к-рых в уравнениях (3) где
где  - известные функции нек-рого параметра t(если t- время, то
- известные функции нек-рого параметра t(если t- время, то  - те моменты времени, в к-рые производились наблюдения). Особенно часто встречается в приложениях случай т. н. параболической интерполяции, когда
- те моменты времени, в к-рые производились наблюдения). Особенно часто встречается в приложениях случай т. н. параболической интерполяции, когда  - многочлены (напр.,
- многочлены (напр.,  ); если
); если 
 а наблюдения равноточные, то для вычисления оценок
а наблюдения равноточные, то для вычисления оценок  можно воспользоваться таблицами ортогональных многочленов. Другой важный для приложений случай - т. н. гармоническая интерполяция, когда в качестве
можно воспользоваться таблицами ортогональных многочленов. Другой важный для приложений случай - т. н. гармоническая интерполяция, когда в качестве  выбирают три-гонометрич. функции (напр.,
выбирают три-гонометрич. функции (напр.,
 ).
).
Пример. Для оценки точности одного из методов химич. анализа этим методом определялась концентрация СаО в десяти эталонных пробах заранее известного состава. Результаты наблюдений указаны в таблице (г - номер эксперимента, t;- истинная концентрация СаО, - концентрация СаО, определенная в результате химич. анализа,
- концентрация СаО, определенная в результате химич. анализа,  - ошибка химич. анализа):
- ошибка химич. анализа):

Если результаты химич. анализа не имеют систематич. ошибок, то  Если же такие ошибки имеются, то в первом приближении их можно представить в виде:
Если же такие ошибки имеются, то в первом приближении их можно представить в виде: (
( наз. постоянной ошибкой, а
наз. постоянной ошибкой, а  - методической ошибкой) или, что то же самое,
- методической ошибкой) или, что то же самое,

где

Для отыскания оценок  и
и  достаточно оценить величины
достаточно оценить величины  и
и  . Условные уравнения в данном случае имеют вид
. Условные уравнения в данном случае имеют вид

поэтому  (согласно предположению о равноточности наблюдений все
(согласно предположению о равноточности наблюдений все  ). Так как
). Так как 
 то система нормальных уравнений записывается особенно просто:
то система нормальных уравнений записывается особенно просто:

где

Дисперсии компонент решения этой системы суть

где k - неизвестная дисперсия на единицу веса (в данном случае k- дисперсия любой из величин  ). Так как в этом примере компоненты решения принимают значения Х 1= -0,35, и Х 2= - 0,00524, то
). Так как в этом примере компоненты решения принимают значения Х 1= -0,35, и Х 2= - 0,00524, то

Если случайные ошибки наблюдений подчиняются нормальному распределению, то отношения  j= 1, 2, распределены по закону Стьюдента. В частности, если результаты наблюдений лишены систематич. ошибок, то
j= 1, 2, распределены по закону Стьюдента. В частности, если результаты наблюдений лишены систематич. ошибок, то  , и, значит, закону Стьюдента должны подчиняться отношения
, и, значит, закону Стьюдента должны подчиняться отношения  и
и  . С помощью таблиц распределения Стьюдента с п-m=8 степенями свободы можно убедиться, что если действительно х 1=х 2=0, то с вероятностью 0,999 каждое из этих отношений не должно превосходить 5,04 и с вероятностью 0,95 не должно превосходить 2,31. В данном случае
. С помощью таблиц распределения Стьюдента с п-m=8 степенями свободы можно убедиться, что если действительно х 1=х 2=0, то с вероятностью 0,999 каждое из этих отношений не должно превосходить 5,04 и с вероятностью 0,95 не должно превосходить 2,31. В данном случае  поэтому гипотезу отсутствия систематич. ошибок целесообразно отвергнуть; в то же время следует признать, что гипотеза об отсутствии ме-тодич. ошибки (
поэтому гипотезу отсутствия систематич. ошибок целесообразно отвергнуть; в то же время следует признать, что гипотеза об отсутствии ме-тодич. ошибки ( ) не противоречит результатам наблюдений, т. к.
) не противоречит результатам наблюдений, т. к.  . Таким образом, можно заключить, что для определения tпо результату наблюдения Тцелесообразно пользоваться приближенной формулой
. Таким образом, можно заключить, что для определения tпо результату наблюдения Тцелесообразно пользоваться приближенной формулой 
Случай нескольких неизвестных (нелинейные связи). Пусть презультатов измерений  связаны с mнеизвестными
связаны с mнеизвестными  функциональной зависимостью
функциональной зависимостью 
 где
где  - независимые случайные ошибки, а функции
- независимые случайные ошибки, а функции  (в общем случае нелинейные) дифференцируемы. Согласно Н. к. м. в качестве оценок для xj принимают такие величины
(в общем случае нелинейные) дифференцируемы. Согласно Н. к. м. в качестве оценок для xj принимают такие величины  , для к-рых сумма квадратов
, для к-рых сумма квадратов

будет наименьшей. Так как функции  нелинейные, то решение нормальных уравнений
нелинейные, то решение нормальных уравнений  в этом случае может представлять значительные трудности. Иногда нелинейные связи каким-либо преобразованием могут быть приведены к линейным.
в этом случае может представлять значительные трудности. Иногда нелинейные связи каким-либо преобразованием могут быть приведены к линейным.
Напр., при намагничивании железа напряженность магнитного поля H связана с магнитной индукцией Вэмпирич. формулой  (коэффициенты
(коэффициенты  и
и  определяются по измеренным значениям
определяются по измеренным значениям  при заданных
при заданных  ). Индукция В- нелинейная функция от
). Индукция В- нелинейная функция от 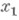 и
и  . Однако обратная величина индукции зависит от
. Однако обратная величина индукции зависит от  и
и  Линейно. Применение Н. к. м. к исходному и преобразованному равенствам дает, вообще говоря, различные оценки для неизвестных
Линейно. Применение Н. к. м. к исходному и преобразованному равенствам дает, вообще говоря, различные оценки для неизвестных  и
и  , но если дисперсия случайных ошибок измерения индукции значительно меньше измеряемых величин
, но если дисперсия случайных ошибок измерения индукции значительно меньше измеряемых величин  , то
, то 
 . Поэтому величинам
. Поэтому величинам  следует приписать веса
следует приписать веса  ; естественно ожидать, что при этих условиях различие оценок в нелинейном и линейном случаях будет практически несущественным.
; естественно ожидать, что при этих условиях различие оценок в нелинейном и линейном случаях будет практически несущественным.
В тех случаях, когда не удается тождественными преобразованиями заменить нелинейные уравнения линейными, пользуются другим способом линеаризации. Из заданных пуравнений отбирают какие-либо m уравнений, решение к-рых  принимают за нулевое приближение для неизвестных xj. Если положить
принимают за нулевое приближение для неизвестных xj. Если положить  то систему условных уравнений можно записать в виде:
то систему условных уравнений можно записать в виде:

Разлагая правые части в ряд по степеням  и ограничиваясь линейными членами, получают
и ограничиваясь линейными членами, получают

где  - значение функции
- значение функции  и ее производных по
и ее производных по  при
при  Эта система уравнений линейна, и поэтому для оценки неизвестных
Эта система уравнений линейна, и поэтому для оценки неизвестных  легко может быть применен Н. к. м. Оценив
легко может быть применен Н. к. м. Оценив  получают первое приближение для неизвестных
получают первое приближение для неизвестных  Величины
Величины  берут за исходное приближение, и всю операцию повторяют, пока с заданной точностью не совпадут два последовательных приближения. Если дисперсии ошибок
берут за исходное приближение, и всю операцию повторяют, пока с заданной точностью не совпадут два последовательных приближения. Если дисперсии ошибок  уменьшаются, то процесс сходится.
уменьшаются, то процесс сходится.
Очень часто при малых  оказывается вполне достаточным уже первое приближение: не имеет смысла требовать нахождения
оказывается вполне достаточным уже первое приближение: не имеет смысла требовать нахождения  с точностью, значительно превышающей
с точностью, значительно превышающей 
Во многих практически важных случаях (и в частности, при оценке сложных нелинейных связей) количество неизвестных параметров бывает весьма большим, и поэтому реализация Н. к. м. оказывается эффективной лишь при использовании современной вычислительной техники.
Лит.:[1] Марков А. А., Исчисление вероятностей, 4 изд., М., 1924; [2] Колмогоров А. Н., "Успехи матем. наук", 1946, т. 1, в. 1, с. 57-70; [3] Линник Ю. В., Метод наименьших квадратов и . основы математико-статистической теории обработки наблюдений, 2 изд., М., 1962; [4] Налимов В. В., Применение математической статистики при анализе вещества, М., 1960; [5] Helmert F. R., Die Ausgleichungsrechnung nach der Methode der kleinsten Quadrate, 3 Aufl., Lpz.- В., 1924.
Л. Н. Большее.

 ее приближенным значением X, вычисленным по результатам наблюдений, пропорционален квадрату ошибки
ее приближенным значением X, вычисленным по результатам наблюдений, пропорционален квадрату ошибки  оптимальной оценкой считается такая лишенная систематич. ошибки величина X, для к-рой среднее значение
оптимальной оценкой считается такая лишенная систематич. ошибки величина X, для к-рой среднее значение  "убытка" минимально. Именно это требование и составляет основу Н. к. м. В общем случае отыскание оптимальной в смысле Н. к. м. оценки X - задача весьма сложная, поэтому практически эту задачу сужают и в качестве Xвыбирают линейную функцию от результатов наблюдений, лишенную систематич. ошибки, и такую, для к-рой среднее значение убытка минимально в классе всех линейных функций. Если случайные ошибки наблюдений подчиняются нормальному распределению и оцениваемая величина mзависит от средних значений результатов наблюдений линейно (случай, весьма часто встречающийся в приложениях Н. к. м.), то решение этой задачи будет одновременно являться и решением общей задачи. При этом оптимальная оценка Xтакже подчиняется нормальному распределению со средним значением
"убытка" минимально. Именно это требование и составляет основу Н. к. м. В общем случае отыскание оптимальной в смысле Н. к. м. оценки X - задача весьма сложная, поэтому практически эту задачу сужают и в качестве Xвыбирают линейную функцию от результатов наблюдений, лишенную систематич. ошибки, и такую, для к-рой среднее значение убытка минимально в классе всех линейных функций. Если случайные ошибки наблюдений подчиняются нормальному распределению и оцениваемая величина mзависит от средних значений результатов наблюдений линейно (случай, весьма часто встречающийся в приложениях Н. к. м.), то решение этой задачи будет одновременно являться и решением общей задачи. При этом оптимальная оценка Xтакже подчиняется нормальному распределению со средним значением  и, следовательно, плотность вероятности случайной величины X
и, следовательно, плотность вероятности случайной величины X
 (это свойство и выражает точное содержание распространенного в теории ошибок утверждения: "оценка X, вычисленная согласно Н. к. м.,- наиболее вероятное значение неизвестного параметра
(это свойство и выражает точное содержание распространенного в теории ошибок утверждения: "оценка X, вычисленная согласно Н. к. м.,- наиболее вероятное значение неизвестного параметра  ").
"). произведено пнезависимых наблюдений, давших результаты
произведено пнезависимых наблюдений, давших результаты 
 - случайные ошибки (по определению, принятому в классич. теории ошибок, случайные ошибки - независимые случайные величины с нулевым математич. ожиданием:
- случайные ошибки (по определению, принятому в классич. теории ошибок, случайные ошибки - независимые случайные величины с нулевым математич. ожиданием:
 ; если же
; если же  наз. систематическими ошибками). Согласно Н. к. м. в качестве оценки величины m. принимают такое X, для к-рого будет наименьшей сумма квадратов (отсюда и само название метода):
наз. систематическими ошибками). Согласно Н. к. м. в качестве оценки величины m. принимают такое X, для к-рого будет наименьшей сумма квадратов (отсюда и само название метода):

 наз. весом, а
наз. весом, а  -квадратичным отклонением измерения с номером
-квадратичным отклонением измерения с номером  . В частности, если все измерения равноточны, то
. В частности, если все измерения равноточны, то  и в этом случае можно положить
и в этом случае можно положить  если же каждое
если же каждое  - арифметич. среднее из
- арифметич. среднее из  равноточных измерений, то полагают
равноточных измерений, то полагают 
 будет наименьшей, если в качестве Xвыбрать взвешенное среднее:
будет наименьшей, если в качестве Xвыбрать взвешенное среднее:
 величины
величины  лишена систематич. ошибки, имеет вес Ри дисперсию
лишена систематич. ошибки, имеет вес Ри дисперсию  . В частности, если все измерения равноточны, то Y - арифметич. среднее результатов измерений:
. В частности, если все измерения равноточны, то Y - арифметич. среднее результатов измерений:
 .В этом случае абсолютная погрешность приближенного равенства
.В этом случае абсолютная погрешность приближенного равенства  меньше
меньше  с вероятностью, близкой к значению интеграла
с вероятностью, близкой к значению интеграла
 ).
). заданы, а множитель кдо наблюдений остается неопределенным, то этот множитель и дисперсия оценки
заданы, а множитель кдо наблюдений остается неопределенным, то этот множитель и дисперсия оценки  могут быть оценены по формулам:
могут быть оценены по формулам:

 подчиняются нормальному распределению, можно найти точное значение вероятности, с к-рой абсолютная погрешность приближенного равенства
подчиняются нормальному распределению, можно найти точное значение вероятности, с к-рой абсолютная погрешность приближенного равенства  окажется меньше
окажется меньше  (t- произвольное положительное число):
(t- произвольное положительное число):
 выбрана таким образом, чтобы выполнялось условие
выбрана таким образом, чтобы выполнялось условие  ( Стьюдента распре деление с п-1 степенями свободы). При больших пформулу (2) можно заменить формулой (1). Однако применение формулы (1) при небольших ппривело бы к грубым ошибкам. Так, напр., согласно (1) значению I= 0,99 соответствует t=2,58; истинные значения t, определяемые при малых пкак решения соответствующих уравнений
( Стьюдента распре деление с п-1 степенями свободы). При больших пформулу (2) можно заменить формулой (1). Однако применение формулы (1) при небольших ппривело бы к грубым ошибкам. Так, напр., согласно (1) значению I= 0,99 соответствует t=2,58; истинные значения t, определяемые при малых пкак решения соответствующих уравнений  приведены в таблице:
приведены в таблице:

 ). Так как все взвешивания равноточные, то следует положить
). Так как все взвешивания равноточные, то следует положить  и в качестве оценки для неизвестного веса
и в качестве оценки для неизвестного веса  выбрать величину
выбрать величину 
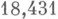 . Задавая, напр.,
. Задавая, напр., по таблицам распределения Стьюдента с девятью степенями свободы можно найти, что
по таблицам распределения Стьюдента с девятью степенями свободы можно найти, что  и поэтому в качестве предельной абсолютной погрешности приближенного равенства
и поэтому в качестве предельной абсолютной погрешности приближенного равенства  следует принять величину
следует принять величину

 связаны с тнеизвестными величинами
связаны с тнеизвестными величинами  независимыми линейными соотношениями
независимыми линейными соотношениями
 - известные коэффициенты, а
- известные коэффициенты, а  - независимые случайные ошибки измерений.
- независимые случайные ошибки измерений. (эту задачу можно рассматривать как обобщение предыдущей, в к-рой
(эту задачу можно рассматривать как обобщение предыдущей, в к-рой
 то средние значения результатов измерений
то средние значения результатов измерений  связаны с неизвестными величинами
связаны с неизвестными величинами  линейными уравнениями (линейные связи):
линейными уравнениями (линейные связи):
 представляют собой решение системы (4), уравнения к-рой предполагаются совместными. Точные значения измеряемых величин
представляют собой решение системы (4), уравнения к-рой предполагаются совместными. Точные значения измеряемых величин  и случайные ошибки
и случайные ошибки  обычно неизвестны, поэтому вместо систем (3) и (4) принято записывать так наз. условные уравнения
обычно неизвестны, поэтому вместо систем (3) и (4) принято записывать так наз. условные уравнения
 применяют такие величины
применяют такие величины  , для к-рых сумма квадратов отклонений
, для к-рых сумма квадратов отклонений
 - вес измерения,
- вес измерения, - величина, обратно пропорциональная дисперсии случайной ошибки
- величина, обратно пропорциональная дисперсии случайной ошибки  ). Условные уравнения, как правило, несовместны, т. с. при любых значениях
). Условные уравнения, как правило, несовместны, т. с. при любых значениях  разности
разности
 , к-рые минимизируют сумму S. В тех исключительных случаях, когда условные уравнения совместны и, значит, обладают решением, это решение совпадает с оценками, полученными согласно Н. к. м.
, к-рые минимизируют сумму S. В тех исключительных случаях, когда условные уравнения совместны и, значит, обладают решением, это решение совпадает с оценками, полученными согласно Н. к. м. ; этот многочлен достигает минимума при таких значениях
; этот многочлен достигает минимума при таких значениях 
 при к-рых обращаются в нуль все первые частные производные:
при к-рых обращаются в нуль все первые частные производные:
 , полученные согласно Н. к. м., должны удовлетворять системе т. н. нормальных уравнений, к-рая в обозначениях, предложенных К. Гауссом, имеет вид
, полученные согласно Н. к. м., должны удовлетворять системе т. н. нормальных уравнений, к-рая в обозначениях, предложенных К. Гауссом, имеет вид


 дисперсии
дисперсии  величин
величин  равны
равны 
 - минор, соответствующий диагональному элементу
- минор, соответствующий диагональному элементу  (иными словами,
(иными словами, - вес оценки
- вес оценки  ). Если множитель пропорциональности (кназ. дисперсией на единицу веса) заранее неизвестен, то для его оценки, а также для оценки дисперсии
). Если множитель пропорциональности (кназ. дисперсией на единицу веса) заранее неизвестен, то для его оценки, а также для оценки дисперсии  служат формулы
служат формулы
 меньше
меньше  с вероятностью, близкой к значению интеграла (1). Если случайные ошибки наблюдений
с вероятностью, близкой к значению интеграла (1). Если случайные ошибки наблюдений  подчиняются нормальному распределению, то все отношения
подчиняются нормальному распределению, то все отношения  распределены по закону Стьюдента с п-то степенями свободы (точная оценка абсолютной погрешности приближенного равенства производится здесь с помощью интеграла (2) так же, как в случае одного неизвестного). Кроме того, минимальное значение суммы Sв вероятностном смысле не зависит от
распределены по закону Стьюдента с п-то степенями свободы (точная оценка абсолютной погрешности приближенного равенства производится здесь с помощью интеграла (2) так же, как в случае одного неизвестного). Кроме того, минимальное значение суммы Sв вероятностном смысле не зависит от  и потому приближенные значения дисперсий оценок
и потому приближенные значения дисперсий оценок  не зависят от самих оценок
не зависят от самих оценок 
 , для к-рых в уравнениях (3)
, для к-рых в уравнениях (3) где
где  - известные функции нек-рого параметра t(если t- время, то
- известные функции нек-рого параметра t(если t- время, то  - те моменты времени, в к-рые производились наблюдения). Особенно часто встречается в приложениях случай т. н. параболической интерполяции, когда
- те моменты времени, в к-рые производились наблюдения). Особенно часто встречается в приложениях случай т. н. параболической интерполяции, когда  - многочлены (напр.,
- многочлены (напр.,  ); если
); если 
 а наблюдения равноточные, то для вычисления оценок
а наблюдения равноточные, то для вычисления оценок  можно воспользоваться таблицами ортогональных многочленов. Другой важный для приложений случай - т. н. гармоническая интерполяция, когда в качестве
можно воспользоваться таблицами ортогональных многочленов. Другой важный для приложений случай - т. н. гармоническая интерполяция, когда в качестве  выбирают три-гонометрич. функции (напр.,
выбирают три-гонометрич. функции (напр.,
 ).
). - концентрация СаО, определенная в результате химич. анализа,
- концентрация СаО, определенная в результате химич. анализа,  - ошибка химич. анализа):
- ошибка химич. анализа):
 Если же такие ошибки имеются, то в первом приближении их можно представить в виде:
Если же такие ошибки имеются, то в первом приближении их можно представить в виде: (
( наз. постоянной ошибкой, а
наз. постоянной ошибкой, а  - методической ошибкой) или, что то же самое,
- методической ошибкой) или, что то же самое,

 и
и  достаточно оценить величины
достаточно оценить величины  и
и  . Условные уравнения в данном случае имеют вид
. Условные уравнения в данном случае имеют вид
 (согласно предположению о равноточности наблюдений все
(согласно предположению о равноточности наблюдений все  ). Так как
). Так как 
 то система нормальных уравнений записывается особенно просто:
то система нормальных уравнений записывается особенно просто:


 ). Так как в этом примере компоненты решения принимают значения Х 1= -0,35, и Х 2= - 0,00524, то
). Так как в этом примере компоненты решения принимают значения Х 1= -0,35, и Х 2= - 0,00524, то
 j= 1, 2, распределены по закону Стьюдента. В частности, если результаты наблюдений лишены систематич. ошибок, то
j= 1, 2, распределены по закону Стьюдента. В частности, если результаты наблюдений лишены систематич. ошибок, то  , и, значит, закону Стьюдента должны подчиняться отношения
, и, значит, закону Стьюдента должны подчиняться отношения  и
и  . С помощью таблиц распределения Стьюдента с п-m=8 степенями свободы можно убедиться, что если действительно х 1=х 2=0, то с вероятностью 0,999 каждое из этих отношений не должно превосходить 5,04 и с вероятностью 0,95 не должно превосходить 2,31. В данном случае
. С помощью таблиц распределения Стьюдента с п-m=8 степенями свободы можно убедиться, что если действительно х 1=х 2=0, то с вероятностью 0,999 каждое из этих отношений не должно превосходить 5,04 и с вероятностью 0,95 не должно превосходить 2,31. В данном случае  поэтому гипотезу отсутствия систематич. ошибок целесообразно отвергнуть; в то же время следует признать, что гипотеза об отсутствии ме-тодич. ошибки (
поэтому гипотезу отсутствия систематич. ошибок целесообразно отвергнуть; в то же время следует признать, что гипотеза об отсутствии ме-тодич. ошибки ( ) не противоречит результатам наблюдений, т. к.
) не противоречит результатам наблюдений, т. к.  . Таким образом, можно заключить, что для определения tпо результату наблюдения Тцелесообразно пользоваться приближенной формулой
. Таким образом, можно заключить, что для определения tпо результату наблюдения Тцелесообразно пользоваться приближенной формулой 
 связаны с mнеизвестными
связаны с mнеизвестными  функциональной зависимостью
функциональной зависимостью 
 где
где  - независимые случайные ошибки, а функции
- независимые случайные ошибки, а функции  (в общем случае нелинейные) дифференцируемы. Согласно Н. к. м. в качестве оценок для xj принимают такие величины
(в общем случае нелинейные) дифференцируемы. Согласно Н. к. м. в качестве оценок для xj принимают такие величины  , для к-рых сумма квадратов
, для к-рых сумма квадратов
 нелинейные, то решение нормальных уравнений
нелинейные, то решение нормальных уравнений  в этом случае может представлять значительные трудности. Иногда нелинейные связи каким-либо преобразованием могут быть приведены к линейным.
в этом случае может представлять значительные трудности. Иногда нелинейные связи каким-либо преобразованием могут быть приведены к линейным. (коэффициенты
(коэффициенты  и
и  определяются по измеренным значениям
определяются по измеренным значениям  при заданных
при заданных  ). Индукция В- нелинейная функция от
). Индукция В- нелинейная функция от 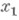 и
и  . Однако обратная величина индукции зависит от
. Однако обратная величина индукции зависит от  и
и  Линейно. Применение Н. к. м. к исходному и преобразованному равенствам дает, вообще говоря, различные оценки для неизвестных
Линейно. Применение Н. к. м. к исходному и преобразованному равенствам дает, вообще говоря, различные оценки для неизвестных  и
и  , но если дисперсия случайных ошибок измерения индукции значительно меньше измеряемых величин
, но если дисперсия случайных ошибок измерения индукции значительно меньше измеряемых величин  , то
, то 
 . Поэтому величинам
. Поэтому величинам  следует приписать веса
следует приписать веса  ; естественно ожидать, что при этих условиях различие оценок в нелинейном и линейном случаях будет практически несущественным.
; естественно ожидать, что при этих условиях различие оценок в нелинейном и линейном случаях будет практически несущественным.  принимают за нулевое приближение для неизвестных xj. Если положить
принимают за нулевое приближение для неизвестных xj. Если положить  то систему условных уравнений можно записать в виде:
то систему условных уравнений можно записать в виде:
 и ограничиваясь линейными членами, получают
и ограничиваясь линейными членами, получают
 - значение функции
- значение функции  и ее производных по
и ее производных по  при
при  Эта система уравнений линейна, и поэтому для оценки неизвестных
Эта система уравнений линейна, и поэтому для оценки неизвестных  легко может быть применен Н. к. м. Оценив
легко может быть применен Н. к. м. Оценив  получают первое приближение для неизвестных
получают первое приближение для неизвестных  Величины
Величины  берут за исходное приближение, и всю операцию повторяют, пока с заданной точностью не совпадут два последовательных приближения. Если дисперсии ошибок
берут за исходное приближение, и всю операцию повторяют, пока с заданной точностью не совпадут два последовательных приближения. Если дисперсии ошибок  уменьшаются, то процесс сходится.
уменьшаются, то процесс сходится. оказывается вполне достаточным уже первое приближение: не имеет смысла требовать нахождения
оказывается вполне достаточным уже первое приближение: не имеет смысла требовать нахождения  с точностью, значительно превышающей
с точностью, значительно превышающей 