|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НАИЛУЧШЕЕ ПРИБЛИЖЕНИЕЗначение НАИЛУЧШЕЕ ПРИБЛИЖЕНИЕ в математической энциклопедии: функции x(t)функциями u(t)из фиксированного множества F- величина
можно рассматривать как заданный на Xфункционал (функционал наилучшего приближения). Функционал Н. п. непрерывен, каково бы ни было множество F. Если F- подпространство, то функционал Н. п. является полунормой, т. е.
и
для любого
В пространстве Xсо строго выпуклой нормой элемент Н. п. единствен. С помощью теорем двойственности Н. п. в линейном нормированном пространстве Xможет быть выражено через верхнюю грань значений нек-рых функционалов из сопряженного пространства
в частности, когда F- подпространство, то
где
где
В пространстве С=С[ а, b]для величины наилучшего равномерного приближения функции О Н. п. в пространстве L1(a, b )см. Маркова критерий. В ряде важных случаев Н. п. функций конечномерным подпространством можно оценить сверху через дифференциально-разностные характеристики (напр., модуль непрерывности) приближаемой функции или ее производных. Понятие наилучшего равномерного приближения непрерывных функций многочленами ввел П. Л. Чебышев (1854), к-рый разработал теоретич. основы Н. п. и установил критерий многочлена Н. п. в метрике пространства С(см. Наилучшего приближения многочлен). Наилучшее приближение класса функций - верхняя грань Н. п. функций f(t)из заданного класса
Величина Пусть В ряде важных случаев, напр, когда Fn - подпространства тригонометрич. полиномов или периодич. сплайнов, а класс Лит.:El] Чебышев П. Л., Полн. собр. соч., т. 2, М.- Л., 1947; [2] Ахиезер Н. И., Лекции по теории аппроксимации, 2 изд., М., 1965; [3] Дзядык В. К., Введение в теорию равномерного приближения функций полиномами, М., 1977; [4] Гончаров В. Л., Теория интерполирования и приближения функций, 2 изд., М., 1954; [5] Корнейчук Н. П., Экстремальные задачи теории приближения, М., 1976; [6] Никольский С. М., Приближение функций многих переменных и теоремы вложения, 2 изд., М., 1977; [7] Тиман А. Ф., Теория приближения функций действительного переменного, М., 1960; [8] Тихомиров В. М., Некоторые вопросы теории приближений, М., 1976; [9] Лоран П. Ж., Аппроксимация и оптимизация, пер. с франц., М., 1975. H. П. Корнейчук, В. П. Моторный. |
|
|
|

 где
где  - погрешность приближения (см. Прибли жения функций мера). Можно говорить о Н. п. в произвольном метрич. пространстве X, когда
- погрешность приближения (см. Прибли жения функций мера). Можно говорить о Н. п. в произвольном метрич. пространстве X, когда  определяется расстоянием между элементами хи и, в этом случае Е( х, F).- расстояние от элемента хдо множества F. Если X- линейное нормированное пространство, то при фиксированном
определяется расстоянием между элементами хи и, в этом случае Е( х, F).- расстояние от элемента хдо множества F. Если X- линейное нормированное пространство, то при фиксированном  Н. п.
Н. п.


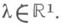 В случае, когда F- конечномерное подпространство, в Fдля любого
В случае, когда F- конечномерное подпространство, в Fдля любого  существует элемент
существует элемент  (элемент наилучшего приближения), на к-ром в (1) реализуется нижняя грань:
(элемент наилучшего приближения), на к-ром в (1) реализуется нижняя грань:
 (см., напр., [5], [8]). Если F- замкнутое выпуклое множество в X, то для любого
(см., напр., [5], [8]). Если F- замкнутое выпуклое множество в X, то для любого 


 - множество функционалов
- множество функционалов  из
из  таких, что f(u)=0 для любого
таких, что f(u)=0 для любого  . В функциональных пространствах Си L р правые части (2) и (3) конкретизируются с учетом формы линейного функционала. В гильбертовом пространстве НН. п. элемента
. В функциональных пространствах Си L р правые части (2) и (3) конкретизируются с учетом формы линейного функционала. В гильбертовом пространстве НН. п. элемента  n -мерным подпространством
n -мерным подпространством  реализуется оператором ортогонального проектирования на
реализуется оператором ортогонального проектирования на  и может быть вычислено:
и может быть вычислено:
 - базис
- базис  - определитель Грама, составленный из скалярных произведений
- определитель Грама, составленный из скалярных произведений  Если базис
Если базис 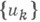 ортонормирован, то
ортонормирован, то
 , n-мерным чебышевским подпространством
, n-мерным чебышевским подпространством  справедлива оценка (теорема Балле Пуссена): если для нек-рой функции
справедлива оценка (теорема Балле Пуссена): если для нек-рой функции  существует n+1 точек
существует n+1 точек  ,
,  в к-рых разность
в к-рых разность  принимает значения с последовательно чередующимися знаками, то
принимает значения с последовательно чередующимися знаками, то 
 фиксированным множеством функций F, т. е. величина
фиксированным множеством функций F, т. е. величина
 характеризует максимальное отклонение (относительно выбранной метрики) класса
характеризует максимальное отклонение (относительно выбранной метрики) класса  от приближающего множества Fи показывает, на какую минимально возможную погрешность можно рассчитывать, приближая произвольную функцию
от приближающего множества Fи показывает, на какую минимально возможную погрешность можно рассчитывать, приближая произвольную функцию  функциями из F.
функциями из F. принадлежит функциональному линейному нормированному пространству
принадлежит функциональному линейному нормированному пространству  - линейно независимая система функций из
- линейно независимая система функций из 
 - подпространства, порожденные первыми п элементами этой системы. Исследование числовой последовательности
- подпространства, порожденные первыми п элементами этой системы. Исследование числовой последовательности  позволяет судить как о структурных и гладкостных характеристиках функций класса
позволяет судить как о структурных и гладкостных характеристиках функций класса 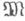 , так и об аппроксимативных свойствах системы Uотносительно класса
, так и об аппроксимативных свойствах системы Uотносительно класса  . Если X- банахово пространство функций и система Uзамкнута в X, т. е.
. Если X- банахово пространство функций и система Uзамкнута в X, т. е.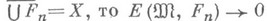 при
при 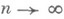 тогда и только тогда, когда
тогда и только тогда, когда 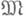 является компактным в X множеством.
является компактным в X множеством. задается ограничениями на норму или модуль непрерывности нек-рой производной
задается ограничениями на норму или модуль непрерывности нек-рой производной  , величины
, величины  точно вычислены [5]. В непериодич. случае имеются результаты, дающие точную асимптотику
точно вычислены [5]. В непериодич. случае имеются результаты, дающие точную асимптотику