|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НАИЛУЧШЕЕ ПОЛНОЕ ПРИБЛИЖЕНИЕЗначение НАИЛУЧШЕЕ ПОЛНОЕ ПРИБЛИЖЕНИЕ в математической энциклопедии: - наилучшее приближение функции Н. п. п. функции
где точная нижняя грань берется по всевозможным тригонометрич. полиномам порядка Наилучшее частное приближение функции
Очевидно, что
Для непрерывных функций двух переменных С. Н. Бернштейн [1] доказал неравенство
где А- абсолютная константа. Установлено [31, что в неравенстве (1) (и в аналогичном соотношении для пространства L1) нельзя заменить
где постоянная Ap,k зависит только от ри k. Аналогично определяются Н. п. п. и наилучшее частное приближение функций, заданных в замкнутой ограниченной области Лит.:[1] Бернштейн С. Н., Собр. соч., т. 2, М., 1954; [2] Тиман А. Ф., Теория приближения функций действительного переменного, М., 1960; [3] Темляков В. Н., "Докл. АН СССР", 1975, т. 223, № 5, с. 1079-82. Н. П. Корнейчук, В. П. Моторный. |
|
|
|

 кпеременных
кпеременных  алгебраическими или тригонометрич. многочленами. Пусть X- пространство Сили
алгебраическими или тригонометрич. многочленами. Пусть X- пространство Сили  2p-периодических по каждому переменному функций
2p-периодических по каждому переменному функций  непрерывных либо суммируемых со степенью
непрерывных либо суммируемых со степенью  на k-мерном кубе периодов.
на k-мерном кубе периодов. тригонометрич. полиномами есть величина
тригонометрич. полиномами есть величина
 от переменных
от переменных 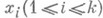 . Наряду с Н. <п. <п. функции f рассматриваются частные наилучшие приближения этой функции.
. Наряду с Н. <п. <п. функции f рассматриваются частные наилучшие приближения этой функции. - есть наилучшее приближение функциями
- есть наилучшее приближение функциями  , являющимися тригонометрич. полиномами степени
, являющимися тригонометрич. полиномами степени 
 соответственно от фиксированных переменных
соответственно от фиксированных переменных  с коэффициентами, зависящими от остальных k- r переменных, т. е. величина
с коэффициентами, зависящими от остальных k- r переменных, т. е. величина


 на множитель, растущий при min
на множитель, растущий при min медленнее. В пространстве
медленнее. В пространстве  имеет место неравенство
имеет место неравенство
 алгебраическими многочленами, и в этом случае известны неравенства вида (1), (2).
алгебраическими многочленами, и в этом случае известны неравенства вида (1), (2).