"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НАИБОЛЕЕ МОЩНЫЙ КРИТЕРИЙ
Значение НАИБОЛЕЕ МОЩНЫЙ КРИТЕРИЙ в математической энциклопедии:
- статистический критерий, имеющий наибольшую мощность среди всех критериев с заданным значимости уровнем. Пусть но результатам наблюдений надлежит проверить простую гипотезу 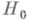 против простой альтернативы
против простой альтернативы 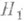 и пусть задана допустимая вероятность
и пусть задана допустимая вероятность 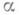 ошибки первого рода, к-рую можно совершить в результате отклонения проверяемой гипотезы
ошибки первого рода, к-рую можно совершить в результате отклонения проверяемой гипотезы 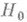 по статистич. критерию, построенному для проверки
по статистич. критерию, построенному для проверки 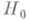 против
против 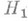 , когда в действительности гипотеза
, когда в действительности гипотеза 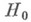 справедлива.
справедлива.
В теории проверки статистич. гипотез наилучшим критерием среди всех статистич. критериев, предназначенных для проверки 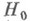 против
против 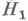 и имеющих одну и ту же вероятность ошибки первого рода или, что то же самое, один и тот же уровень значимости
и имеющих одну и ту же вероятность ошибки первого рода или, что то же самое, один и тот же уровень значимости 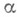 , является тот критерий, к-рый имеет наибольшую мощность; т. е. наилучший критерий с наибольшей вероятностью отклоняет проверяемую гипотезу
, является тот критерий, к-рый имеет наибольшую мощность; т. е. наилучший критерий с наибольшей вероятностью отклоняет проверяемую гипотезу 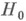 , когда справедлива конкурирующая гипотеза
, когда справедлива конкурирующая гипотеза 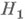 . Именно этот наилучший критерий наз. Н. м. к. уровня
. Именно этот наилучший критерий наз. Н. м. к. уровня 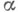 среди всех статистич. критериев уровня
среди всех статистич. критериев уровня 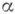 , предназначенных для проверки простой гипотезы
, предназначенных для проверки простой гипотезы 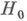 против простой альтернативы
против простой альтернативы 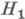 Так как мощность статистич. критерия равна дополнению до единицы вероятности ошибки второго рода, к-рую можно совершить, принимая
Так как мощность статистич. критерия равна дополнению до единицы вероятности ошибки второго рода, к-рую можно совершить, принимая 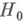 , когда она в действительности неверна, то понятие Н. м. к. часто формулируют в терминах вероятностей ошибок первого и второго рода: Н. м. к.- статистич. критерий, предназначенный для проверки простой гипотезы против простой альтернативы и к-рый имеет наименьшую вероятность ошибки второго рода среди всех статистич. критериев с заданной вероятностью ошибки первого рода. Решение задачи о построении Н. м. к. в случае простых гипотез дается Неймана- Пирсона леммой, согласно к-рой отношения правдоподобия критерий является Н. м. к.
, когда она в действительности неверна, то понятие Н. м. к. часто формулируют в терминах вероятностей ошибок первого и второго рода: Н. м. к.- статистич. критерий, предназначенный для проверки простой гипотезы против простой альтернативы и к-рый имеет наименьшую вероятность ошибки второго рода среди всех статистич. критериев с заданной вероятностью ошибки первого рода. Решение задачи о построении Н. м. к. в случае простых гипотез дается Неймана- Пирсона леммой, согласно к-рой отношения правдоподобия критерий является Н. м. к.
В случае, когда конкурирующие гипотезы 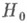 и
и 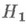 являются сложными, задача построения Н. м. к. формулируется в терминах равномерно наиболее мощного критерия, если таковой существует.
являются сложными, задача построения Н. м. к. формулируется в терминах равномерно наиболее мощного критерия, если таковой существует.
Лит.:[1] Леман Э. Л., Проверка статистических гипотез, пер. с англ., 2 изд., М., 1979; [2] Nеуman J., Pearson E.,"Phil. Trans. Roy. Soc. London, A", 1933, v. 231, p. 289- 337.
M. С. Никулин.

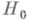 против простой альтернативы
против простой альтернативы 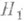 и пусть задана допустимая вероятность
и пусть задана допустимая вероятность 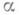 ошибки первого рода, к-рую можно совершить в результате отклонения проверяемой гипотезы
ошибки первого рода, к-рую можно совершить в результате отклонения проверяемой гипотезы 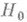 по статистич. критерию, построенному для проверки
по статистич. критерию, построенному для проверки 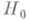 против
против 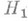 , когда в действительности гипотеза
, когда в действительности гипотеза 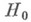 справедлива.
справедлива.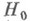 против
против 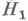 и имеющих одну и ту же вероятность ошибки первого рода или, что то же самое, один и тот же уровень значимости
и имеющих одну и ту же вероятность ошибки первого рода или, что то же самое, один и тот же уровень значимости 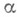 , является тот критерий, к-рый имеет наибольшую мощность; т. е. наилучший критерий с наибольшей вероятностью отклоняет проверяемую гипотезу
, является тот критерий, к-рый имеет наибольшую мощность; т. е. наилучший критерий с наибольшей вероятностью отклоняет проверяемую гипотезу 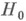 , когда справедлива конкурирующая гипотеза
, когда справедлива конкурирующая гипотеза 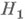 . Именно этот наилучший критерий наз. Н. м. к. уровня
. Именно этот наилучший критерий наз. Н. м. к. уровня 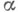 среди всех статистич. критериев уровня
среди всех статистич. критериев уровня 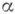 , предназначенных для проверки простой гипотезы
, предназначенных для проверки простой гипотезы 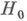 против простой альтернативы
против простой альтернативы 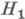 Так как мощность статистич. критерия равна дополнению до единицы вероятности ошибки второго рода, к-рую можно совершить, принимая
Так как мощность статистич. критерия равна дополнению до единицы вероятности ошибки второго рода, к-рую можно совершить, принимая 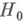 , когда она в действительности неверна, то понятие Н. м. к. часто формулируют в терминах вероятностей ошибок первого и второго рода: Н. м. к.- статистич. критерий, предназначенный для проверки простой гипотезы против простой альтернативы и к-рый имеет наименьшую вероятность ошибки второго рода среди всех статистич. критериев с заданной вероятностью ошибки первого рода. Решение задачи о построении Н. м. к. в случае простых гипотез дается Неймана- Пирсона леммой, согласно к-рой отношения правдоподобия критерий является Н. м. к.
, когда она в действительности неверна, то понятие Н. м. к. часто формулируют в терминах вероятностей ошибок первого и второго рода: Н. м. к.- статистич. критерий, предназначенный для проверки простой гипотезы против простой альтернативы и к-рый имеет наименьшую вероятность ошибки второго рода среди всех статистич. критериев с заданной вероятностью ошибки первого рода. Решение задачи о построении Н. м. к. в случае простых гипотез дается Неймана- Пирсона леммой, согласно к-рой отношения правдоподобия критерий является Н. м. к.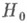 и
и 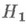 являются сложными, задача построения Н. м. к. формулируется в терминах равномерно наиболее мощного критерия, если таковой существует.
являются сложными, задача построения Н. м. к. формулируется в терминах равномерно наиболее мощного критерия, если таковой существует.