"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НАДЕЖНОСТЬ И КОНТРОЛЬ УПРАВЛЯЮЩИХ
Значение НАДЕЖНОСТЬ И КОНТРОЛЬ УПРАВЛЯЮЩИХ в математической энциклопедии:
СИСТЕМ, проблемы надежности управляющих систем,- одно из направлений теории управляющих систем, к-рое изучает управляющие системы, подверженные помехам.
Пусть  - нек-рый класс управляющих систем (у. с.) и пусть имеется источник помех, или источник неисправностей, к-рый, воздействуя на у. с.
- нек-рый класс управляющих систем (у. с.) и пусть имеется источник помех, или источник неисправностей, к-рый, воздействуя на у. с.  ,. переводит ее в у. с.
,. переводит ее в у. с.  из нек-рого класса
из нек-рого класса 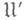 Если допустить, что источник помех может также сохранять у. с. неизменной, напр.
Если допустить, что источник помех может также сохранять у. с. неизменной, напр.
Пусть каждая у. с. из  вполне определяется своей схемой
вполне определяется своей схемой  , тогда воздействие источника помех сводится к воздействию на ее схему
, тогда воздействие источника помех сводится к воздействию на ее схему  . Источник неисправностей преобразует схему, что может проявляться: а) путем нарушения работы элементов, т.e. изменением элементов; б) путем изменения соединений элементов и т. п. В результате действия источника неисправностей исходная схема,
. Источник неисправностей преобразует схему, что может проявляться: а) путем нарушения работы элементов, т.e. изменением элементов; б) путем изменения соединений элементов и т. п. В результате действия источника неисправностей исходная схема, у. с.
у. с. переходит в "неисправные" состояния
переходит в "неисправные" состояния  определяющие соответственно у. с.
определяющие соответственно у. с. Пусть этим схемам соответствуют функции
Пусть этим схемам соответствуют функции  наз. также функциями неисправностей (здесь
наз. также функциями неисправностей (здесь  характеризует функционирование у. с.
характеризует функционирование у. с. ). Обычно источник неисправностей дополнительно характеризуется либо распределением вероятностей ошибок, либо ограничениями невозможное число элементарных неисправностей.
). Обычно источник неисправностей дополнительно характеризуется либо распределением вероятностей ошибок, либо ограничениями невозможное число элементарных неисправностей.
Проблемы надежности рассматриваются в основном для трех классов у. с: схем из функциональных элементов, контактных схем и автоматов.
Пусть 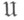 - класс схем из функциональных элементов, принадлежащих данному базису Б, где
- класс схем из функциональных элементов, принадлежащих данному базису Б, где  и
и  . В случае, если источник неисправностей воздействует только на элементы схемы, то он преобразует элементы
. В случае, если источник неисправностей воздействует только на элементы схемы, то он преобразует элементы  из
из  в элементы с таким же числом входов, как и
в элементы с таким же числом входов, как и  , но, быть может, с иным функционированием, а элементы из
, но, быть может, с иным функционированием, а элементы из  оставляет неизменными. Таким образом,
оставляет неизменными. Таким образом,  состоит из ненадежных, а
состоит из ненадежных, а  - из надежных элементов. В этом Случае источник можно характеризовать вероятностями
- из надежных элементов. В этом Случае источник можно характеризовать вероятностями 
 выхода из строя соответственно элементов
выхода из строя соответственно элементов 
 . Напр.,
. Напр., состоит из инверторов, конъюнкторов. и дизъюнкторов, а
состоит из инверторов, конъюнкторов. и дизъюнкторов, а  - из элементов голосования, реализующих соответственно функции
- из элементов голосования, реализующих соответственно функции  и
и  При этом можно положить, что
При этом можно положить, что  - вероятность выхода из строя элементов из
- вероятность выхода из строя элементов из  .
.
В случае, когда  - класс контактных схем, рассматривают источник неисправностей, к-рый в качестве элементарных неисправностей дает либо короткое замыкание контакта, либо разрыв контакта. При этом дополнительно предполагают, что для контактных схем, реализующих функции от ппеременных, возможно не более
- класс контактных схем, рассматривают источник неисправностей, к-рый в качестве элементарных неисправностей дает либо короткое замыкание контакта, либо разрыв контакта. При этом дополнительно предполагают, что для контактных схем, реализующих функции от ппеременных, возможно не более  элементарных повреждений.
элементарных повреждений.
В проблематике Н. и к. у. с. можно выделить три направления.
I. Построение надежных схем из ненадежных элементов. Это направление развито для двух классов у. с.: контактных схем и схем из функциональных элементов. В случае схем из функциональных элементов схема  характеризуется нек-рой вероятностью ртех случаев, когда она функционирует неправильно. Здесь рассматривают два основных вопроса.
характеризуется нек-рой вероятностью ртех случаев, когда она функционирует неправильно. Здесь рассматривают два основных вопроса.
1) Какими свойствами должен обладать базис Б, чтобы для любой булевой функции  и любого
и любого  можно было построить схему
можно было построить схему  , реализующую
, реализующую  и такую, что вероятность рсе неправильной работы была бы меньше
и такую, что вероятность рсе неправильной работы была бы меньше  , т. е. каждая булева функция допускала бы сколь угодно надежную реализацию.
, т. е. каждая булева функция допускала бы сколь угодно надежную реализацию.
Установлено, что существуют базисы, в к-рых для любой функции возможна сколь угодно надежная реализация. Примером такого базиса является базис Б (см. выше): состоит из инверторов, конъюнкторов и дизъюнкторов с вероятностью ошибки
состоит из инверторов, конъюнкторов и дизъюнкторов с вероятностью ошибки  состоит нз абсолютно надежного элемента голосования. Найдены необходимые и достаточные условия на базис
состоит нз абсолютно надежного элемента голосования. Найдены необходимые и достаточные условия на базис  при к-рых возможно построение сколь угодно надежных схем для всех булевых функций.
при к-рых возможно построение сколь угодно надежных схем для всех булевых функций.
2) Построение метода синтеза минимальных (или в том или ином смысле близких к минимальным) схем, реализующих булевы функции, ненадежность к-рых не превосходит заданной величины  . Оказывается (напр., для предыдущего базиса с
. Оказывается (напр., для предыдущего базиса с  ), что можно построить метод синтеза схем, к-рый для большинства булевых функций и данного
), что можно построить метод синтеза схем, к-рый для большинства булевых функций и данного  дает асимптотически (по п)минимальные схемы. В частности, для функции Шеннона
дает асимптотически (по п)минимальные схемы. В частности, для функции Шеннона  выражающей ' минимальное число элементов из Б (см. пример выше), достаточное для реализации любой булевой функции от ппеременных с ненадежностью, не большей
выражающей ' минимальное число элементов из Б (см. пример выше), достаточное для реализации любой булевой функции от ппеременных с ненадежностью, не большей  , получена асимптотика
, получена асимптотика

II. Построение самокорректирующихся схем. Это направление наиболее полно изучено для двух классов у. с.- контактных схем и схем из функциональных элементов. Здесь источник неисправностей характеризуется ограничениями на число элементарных повреждений. Считается, что в пределах рассмотрений дальнейших изменений в схеме не происходит. Схема  , реализующая функцию
, реализующая функцию  , наз. самокорректирующейся относительно данного источника неисправностей, если
, наз. самокорректирующейся относительно данного источника неисправностей, если 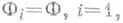
 Другими словами, самокорректирующаяся схема функционирует правильно, несмотря на воздействие источника неис
Другими словами, самокорректирующаяся схема функционирует правильно, несмотря на воздействие источника неис

правностей. Напр., контактная схема на рис. 1, реализующая функцию  является самокорректирующейся относительно источника, вызывающего не более одного разрыва контакта. Основными задачами этого направления являются: 1) выяснение условий, при к-рых существуют самокорректирующиеся схемы, и 2) разработка методов синтеза минимальных (или в том или ином смысле близких к минимальным) самокорректирующихся схем. Ниже показано решение этих задач на примере контактных схем с источником неисправностей, вызывающим не более
является самокорректирующейся относительно источника, вызывающего не более одного разрыва контакта. Основными задачами этого направления являются: 1) выяснение условий, при к-рых существуют самокорректирующиеся схемы, и 2) разработка методов синтеза минимальных (или в том или ином смысле близких к минимальным) самокорректирующихся схем. Ниже показано решение этих задач на примере контактных схем с источником неисправностей, вызывающим не более  замыканий и разрывов.
замыканий и разрывов.
Оказывается, что для любой булевой функции 
 можно построить самокорректирующуюся относительно этого источника неисправностей схему. Для этого достаточно взять любую контактную схему
можно построить самокорректирующуюся относительно этого источника неисправностей схему. Для этого достаточно взять любую контактную схему  , реализующую
, реализующую  , и в ней каждый контакт
, и в ней каждый контакт  заменить на подсхему, состоящую из
заменить на подсхему, состоящую из  последовательно соединенных одинаковых блоков, каждый из к-рых является параллельным соединением
последовательно соединенных одинаковых блоков, каждый из к-рых является параллельным соединением  экземпляров данного контакта
экземпляров данного контакта  . Такую схему наз. тривиальной самокорректирующейся схемой. Построенная самокорректирующаяся схема будет в
. Такую схему наз. тривиальной самокорректирующейся схемой. Построенная самокорректирующаяся схема будет в  раз сложнее исходной. Предыдущий пример (рис. 1) показывает, что существуют и нетривиальные самокорректирующиеся схемы.
раз сложнее исходной. Предыдущий пример (рис. 1) показывает, что существуют и нетривиальные самокорректирующиеся схемы.
Задача построения самокорректирующихся схем - специальная задача синтеза у. с. с дополнительными требованиями. Главный результат здесь состоит в том, что для большинс-тва булевых функций  можно построить самокорректирующуюся схему (относительно нек-рого класса источников), сложность к-рой асимптотически (при
можно построить самокорректирующуюся схему (относительно нек-рого класса источников), сложность к-рой асимптотически (при  ) равна сложности минимальной схемы, реализующей f без требования самокоррекции. Здесь показано, что при нек-рых ограничениях на порядок роста
) равна сложности минимальной схемы, реализующей f без требования самокоррекции. Здесь показано, что при нек-рых ограничениях на порядок роста  имеет место следующая асимптотика для функции Шеннона
имеет место следующая асимптотика для функции Шеннона

III. Контроль управляющих систем. Это направление наиболее полно изучено для трех классов у. с: контактных схем, схем из функциональных элементов и автоматов. Рассмотрение проблем контроля у. с. предполагает: 1) наличие источника неисправностей, к-рый, совершив воздействие на у. с, в течение нек-рого промежутка удерживает неисправное состояние исходной у. с. и не производит других повреждений; 2) задание цели контроля. Последняя определяется как распознавание нек-рого свойства данной у. с. Напр., выяснение, является ли данная у. с. исправной или нет (задача о проверке), или, в случае, если у. с. неисправна, нахождение неисправности (задача о диагностике); 3) фиксацию средств контроля. Контроль может происходить либо без вмешательства в схему, либо допускается возможность вмешательства. Напр., замена элементов на эталонные, перестановка однотипных блоков, использование дополнительных контрольных точек в схеме и т. п. Средства контроля включают в себя также процедуру получения информации о контролируемом объекте. Ими являются эксперименты, к-рые делятся на безусловные и условные. В безусловных экспериментах последовательности, подаваемые на вход контролирующего устройства, определяются заранее и не зависят от последовательности на его выходе. В условных экспериментах каждый последующий символ входной последовательности может выбираться в зависимости от символов, появившихся на выходе в предшествующие моменты времени.
Совокупность экспериментов, позволяющая распознать данное свойство, наз. тестом. Так как обычно существует много различных тестов, распознающих требуемое свойство, то на множестве тестов вводят меру сложности и ищут тест, имеющий минимальную сложность. Основная задача состоит здесь в том, чтобы для каждого свойства уметь строить минимальные или близкие к ним тесты. Эта задача является частью более общей проблемы - построения компактных алгоритмов распознавания тех или иных свойств.
Проследим решение этих задач на примере контактных схем и схем из функциональных элементов для случая, когда нет вмешательства в схему. Исходным пунктом здесь являются функции неисправностей  схемы
схемы  , реализующей
, реализующей  , причем
, причем  При этом возможен случай
При этом возможен случай  для нек-рых пар
для нек-рых пар  что означа-
что означа-
ет неразличимость i- йи j- йнеисправностей. Таким образом, множество функций  разбивается на классы эквивалентности
разбивается на классы эквивалентности  такие, что
такие, что  принадлежат одному классу тогда и только тогда, когда
принадлежат одному классу тогда и только тогда, когда  причем
причем  принадлежит классу
принадлежит классу  . Неисправности, приводящие к функциям из одного класса, неразличимы. Классы
. Неисправности, приводящие к функциям из одного класса, неразличимы. Классы  приводят к таблице функции неисправностей.
приводят к таблице функции неисправностей.
Пример. Контактная схема (рис. 2) реализует функцию

источник помех вызывает не более одного разрыва. Здесь 

 Таким образом, имеем семь классов:
Таким образом, имеем семь классов:

 к-рые дают таблицу функций неисправностей (см. таблицу). Свойство, подлежащее распознаванию, обычно задают через подмножество
к-рые дают таблицу функций неисправностей (см. таблицу). Свойство, подлежащее распознаванию, обычно задают через подмножество  пар
пар  но
но
меров классов функций неисправностей, к-рые требуется отличать

. Если, напр.,

то свойство выражает отличимость исправной схемы от любого неисправного состояния (задача проверки).
Если 
то требуется уметь отличать каждое состояние схемы от любого другого (задача о диагностике). Наконец, если
 то имеют дело с задачей о диагностике "блока", т. е. с задачей выяснения, в какой части схемы находится поврежденный элемент.
то имеют дело с задачей о диагностике "блока", т. е. с задачей выяснения, в какой части схемы находится поврежденный элемент.

Пусть  - множество наборов, на к-рых определены функции
- множество наборов, на к-рых определены функции  . Совокупность наборов
. Совокупность наборов  наз. тестом для данной таблицы функций неисправностей относительно подмножества
наз. тестом для данной таблицы функций неисправностей относительно подмножества  , если для любой пары
, если для любой пары  из
из  существует набор еиз Ттакой, что
существует набор еиз Ттакой, что  Тест Тназ. минимальны м, если он содержит наименьшее число наборов. Тест Тназ. тупиковым, если при удалении любого набора е из Т получается подмножество наборов, не являющееся тестом. Множество
Тест Тназ. минимальны м, если он содержит наименьшее число наборов. Тест Тназ. тупиковым, если при удалении любого набора е из Т получается подмножество наборов, не являющееся тестом. Множество  является тестом (тривиальным тестом). Минимальный тест является тупиковым. Проблема нахождения минимального теста связана с необходимостью сокращения времени контроля.
является тестом (тривиальным тестом). Минимальный тест является тупиковым. Проблема нахождения минимального теста связана с необходимостью сокращения времени контроля.
Существует алгоритм для нахождения всех тупиковых (значит и минимальных) тестов. Пусть 
 - множество всех наборов, на к-рых отличаются
- множество всех наборов, на к-рых отличаются  и
и  . Если в выражении
. Если в выражении  совершить умножение по правилам булевой алгебры и затем удалить "поглощаемые" члены, пользуясь соотношением
совершить умножение по правилам булевой алгебры и затем удалить "поглощаемые" члены, пользуясь соотношением  то оставшиеся произведения будут соответствовать тупиковым тестам. Так, если для рассмотренного выше примера взять задачу проверки
то оставшиеся произведения будут соответствовать тупиковым тестам. Так, если для рассмотренного выше примера взять задачу проверки 
то указанный алгоритм дает:

Имеется пять тупиковых тестов: T1={e1,e3,e5}, T2={e2,e4,e6}, T3={e1,e2,e4,e5}, T4={e1,e3,e4,e6}, T5={e2,e3,e5,e6}из к-рых  являются минимальными. Описанный алгоритм может быть применен для обнаружения ошибок при монтаже в соединениях элементов. Данный алгоритм с небольшими модификациями годится также для построения тупиковых кратных экспериментов для автоматов. Эффективность алгоритма построения тупиковых тестов резко падает с увеличением размеров таблицы функций неисправностей. Повышение эффективности связано с учетом строения таблицы, а также с учетом информации о структуре схемы. В этом направлении построена серия методов. Другие аспекты Н. и к. у. с. развиваются в рамках теории вероятностей.
являются минимальными. Описанный алгоритм может быть применен для обнаружения ошибок при монтаже в соединениях элементов. Данный алгоритм с небольшими модификациями годится также для построения тупиковых кратных экспериментов для автоматов. Эффективность алгоритма построения тупиковых тестов резко падает с увеличением размеров таблицы функций неисправностей. Повышение эффективности связано с учетом строения таблицы, а также с учетом информации о структуре схемы. В этом направлении построена серия методов. Другие аспекты Н. и к. у. с. развиваются в рамках теории вероятностей.
Лит.:[1] Чегис И. А., Яблонский С. В., "Тр. Матем. ин-та АН СССР", 1958, т. 51, с. 270-360; [2] Соловьев Н. А., Тесты, Новосиб., 1978; [3] По т а и о в Ю. Г., Яблонский С. В., "Докл. АН СССР", 1960, т. 134, №3, с. 544-47; [4] Нейман Дж., в кн.: Автоматы, М., 1956, с. 68-139; [5] Мур Э. Ф, Шеннон К. Э., Кибернетический сборник, п. 1, М., 1960, с. 109-48.
С. В. Яблонский.

 - нек-рый класс управляющих систем (у. с.) и пусть имеется источник помех, или источник неисправностей, к-рый, воздействуя на у. с.
- нек-рый класс управляющих систем (у. с.) и пусть имеется источник помех, или источник неисправностей, к-рый, воздействуя на у. с.  ,. переводит ее в у. с.
,. переводит ее в у. с.  из нек-рого класса
из нек-рого класса 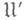 Если допустить, что источник помех может также сохранять у. с. неизменной, напр.
Если допустить, что источник помех может также сохранять у. с. неизменной, напр.
 вполне определяется своей схемой
вполне определяется своей схемой  , тогда воздействие источника помех сводится к воздействию на ее схему
, тогда воздействие источника помех сводится к воздействию на ее схему  . Источник неисправностей преобразует схему, что может проявляться: а) путем нарушения работы элементов, т.e. изменением элементов; б) путем изменения соединений элементов и т. п. В результате действия источника неисправностей исходная схема,
. Источник неисправностей преобразует схему, что может проявляться: а) путем нарушения работы элементов, т.e. изменением элементов; б) путем изменения соединений элементов и т. п. В результате действия источника неисправностей исходная схема, у. с.
у. с. переходит в "неисправные" состояния
переходит в "неисправные" состояния  определяющие соответственно у. с.
определяющие соответственно у. с. Пусть этим схемам соответствуют функции
Пусть этим схемам соответствуют функции  наз. также функциями неисправностей (здесь
наз. также функциями неисправностей (здесь  характеризует функционирование у. с.
характеризует функционирование у. с. ). Обычно источник неисправностей дополнительно характеризуется либо распределением вероятностей ошибок, либо ограничениями невозможное число элементарных неисправностей.
). Обычно источник неисправностей дополнительно характеризуется либо распределением вероятностей ошибок, либо ограничениями невозможное число элементарных неисправностей.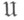 - класс схем из функциональных элементов, принадлежащих данному базису Б, где
- класс схем из функциональных элементов, принадлежащих данному базису Б, где  и
и  . В случае, если источник неисправностей воздействует только на элементы схемы, то он преобразует элементы
. В случае, если источник неисправностей воздействует только на элементы схемы, то он преобразует элементы  из
из  в элементы с таким же числом входов, как и
в элементы с таким же числом входов, как и  , но, быть может, с иным функционированием, а элементы из
, но, быть может, с иным функционированием, а элементы из  оставляет неизменными. Таким образом,
оставляет неизменными. Таким образом,  состоит из ненадежных, а
состоит из ненадежных, а  - из надежных элементов. В этом Случае источник можно характеризовать вероятностями
- из надежных элементов. В этом Случае источник можно характеризовать вероятностями 
 выхода из строя соответственно элементов
выхода из строя соответственно элементов 
 . Напр.,
. Напр., состоит из инверторов, конъюнкторов. и дизъюнкторов, а
состоит из инверторов, конъюнкторов. и дизъюнкторов, а  - из элементов голосования, реализующих соответственно функции
- из элементов голосования, реализующих соответственно функции  и
и  При этом можно положить, что
При этом можно положить, что  - вероятность выхода из строя элементов из
- вероятность выхода из строя элементов из  .
. - класс контактных схем, рассматривают источник неисправностей, к-рый в качестве элементарных неисправностей дает либо короткое замыкание контакта, либо разрыв контакта. При этом дополнительно предполагают, что для контактных схем, реализующих функции от ппеременных, возможно не более
- класс контактных схем, рассматривают источник неисправностей, к-рый в качестве элементарных неисправностей дает либо короткое замыкание контакта, либо разрыв контакта. При этом дополнительно предполагают, что для контактных схем, реализующих функции от ппеременных, возможно не более  элементарных повреждений.
элементарных повреждений. характеризуется нек-рой вероятностью ртех случаев, когда она функционирует неправильно. Здесь рассматривают два основных вопроса.
характеризуется нек-рой вероятностью ртех случаев, когда она функционирует неправильно. Здесь рассматривают два основных вопроса. и любого
и любого  можно было построить схему
можно было построить схему  , реализующую
, реализующую  и такую, что вероятность рсе неправильной работы была бы меньше
и такую, что вероятность рсе неправильной работы была бы меньше  , т. е. каждая булева функция допускала бы сколь угодно надежную реализацию.
, т. е. каждая булева функция допускала бы сколь угодно надежную реализацию. состоит из инверторов, конъюнкторов и дизъюнкторов с вероятностью ошибки
состоит из инверторов, конъюнкторов и дизъюнкторов с вероятностью ошибки  состоит нз абсолютно надежного элемента голосования. Найдены необходимые и достаточные условия на базис
состоит нз абсолютно надежного элемента голосования. Найдены необходимые и достаточные условия на базис  при к-рых возможно построение сколь угодно надежных схем для всех булевых функций.
при к-рых возможно построение сколь угодно надежных схем для всех булевых функций. . Оказывается (напр., для предыдущего базиса с
. Оказывается (напр., для предыдущего базиса с  ), что можно построить метод синтеза схем, к-рый для большинства булевых функций и данного
), что можно построить метод синтеза схем, к-рый для большинства булевых функций и данного  дает асимптотически (по п)минимальные схемы. В частности, для функции Шеннона
дает асимптотически (по п)минимальные схемы. В частности, для функции Шеннона  выражающей ' минимальное число элементов из Б (см. пример выше), достаточное для реализации любой булевой функции от ппеременных с ненадежностью, не большей
выражающей ' минимальное число элементов из Б (см. пример выше), достаточное для реализации любой булевой функции от ппеременных с ненадежностью, не большей  , получена асимптотика
, получена асимптотика
 , реализующая функцию
, реализующая функцию  , наз. самокорректирующейся относительно данного источника неисправностей, если
, наз. самокорректирующейся относительно данного источника неисправностей, если 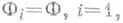
 Другими словами, самокорректирующаяся схема функционирует правильно, несмотря на воздействие источника неис
Другими словами, самокорректирующаяся схема функционирует правильно, несмотря на воздействие источника неис
 является самокорректирующейся относительно источника, вызывающего не более одного разрыва контакта. Основными задачами этого направления являются: 1) выяснение условий, при к-рых существуют самокорректирующиеся схемы, и 2) разработка методов синтеза минимальных (или в том или ином смысле близких к минимальным) самокорректирующихся схем. Ниже показано решение этих задач на примере контактных схем с источником неисправностей, вызывающим не более
является самокорректирующейся относительно источника, вызывающего не более одного разрыва контакта. Основными задачами этого направления являются: 1) выяснение условий, при к-рых существуют самокорректирующиеся схемы, и 2) разработка методов синтеза минимальных (или в том или ином смысле близких к минимальным) самокорректирующихся схем. Ниже показано решение этих задач на примере контактных схем с источником неисправностей, вызывающим не более  замыканий и разрывов.
замыканий и разрывов.
 можно построить самокорректирующуюся относительно этого источника неисправностей схему. Для этого достаточно взять любую контактную схему
можно построить самокорректирующуюся относительно этого источника неисправностей схему. Для этого достаточно взять любую контактную схему  , реализующую
, реализующую  , и в ней каждый контакт
, и в ней каждый контакт  заменить на подсхему, состоящую из
заменить на подсхему, состоящую из  последовательно соединенных одинаковых блоков, каждый из к-рых является параллельным соединением
последовательно соединенных одинаковых блоков, каждый из к-рых является параллельным соединением  экземпляров данного контакта
экземпляров данного контакта  . Такую схему наз. тривиальной самокорректирующейся схемой. Построенная самокорректирующаяся схема будет в
. Такую схему наз. тривиальной самокорректирующейся схемой. Построенная самокорректирующаяся схема будет в  раз сложнее исходной. Предыдущий пример (рис. 1) показывает, что существуют и нетривиальные самокорректирующиеся схемы.
раз сложнее исходной. Предыдущий пример (рис. 1) показывает, что существуют и нетривиальные самокорректирующиеся схемы. можно построить самокорректирующуюся схему (относительно нек-рого класса источников), сложность к-рой асимптотически (при
можно построить самокорректирующуюся схему (относительно нек-рого класса источников), сложность к-рой асимптотически (при  ) равна сложности минимальной схемы, реализующей f без требования самокоррекции. Здесь показано, что при нек-рых ограничениях на порядок роста
) равна сложности минимальной схемы, реализующей f без требования самокоррекции. Здесь показано, что при нек-рых ограничениях на порядок роста  имеет место следующая асимптотика для функции Шеннона
имеет место следующая асимптотика для функции Шеннона
 схемы
схемы  , реализующей
, реализующей  , причем
, причем  При этом возможен случай
При этом возможен случай  для нек-рых пар
для нек-рых пар  что означа-
что означа- разбивается на классы эквивалентности
разбивается на классы эквивалентности  такие, что
такие, что  принадлежат одному классу тогда и только тогда, когда
принадлежат одному классу тогда и только тогда, когда  причем
причем  принадлежит классу
принадлежит классу  . Неисправности, приводящие к функциям из одного класса, неразличимы. Классы
. Неисправности, приводящие к функциям из одного класса, неразличимы. Классы  приводят к таблице функции неисправностей.
приводят к таблице функции неисправностей.


 Таким образом, имеем семь классов:
Таким образом, имеем семь классов:

 к-рые дают таблицу функций неисправностей (см. таблицу). Свойство, подлежащее распознаванию, обычно задают через подмножество
к-рые дают таблицу функций неисправностей (см. таблицу). Свойство, подлежащее распознаванию, обычно задают через подмножество  пар
пар  но
но 


 то имеют дело с задачей о диагностике "блока", т. е. с задачей выяснения, в какой части схемы находится поврежденный элемент.
то имеют дело с задачей о диагностике "блока", т. е. с задачей выяснения, в какой части схемы находится поврежденный элемент.
 - множество наборов, на к-рых определены функции
- множество наборов, на к-рых определены функции  . Совокупность наборов
. Совокупность наборов  наз. тестом для данной таблицы функций неисправностей относительно подмножества
наз. тестом для данной таблицы функций неисправностей относительно подмножества  , если для любой пары
, если для любой пары  из
из  существует набор еиз Ттакой, что
существует набор еиз Ттакой, что  Тест Тназ. минимальны м, если он содержит наименьшее число наборов. Тест Тназ. тупиковым, если при удалении любого набора е из Т получается подмножество наборов, не являющееся тестом. Множество
Тест Тназ. минимальны м, если он содержит наименьшее число наборов. Тест Тназ. тупиковым, если при удалении любого набора е из Т получается подмножество наборов, не являющееся тестом. Множество  является тестом (тривиальным тестом). Минимальный тест является тупиковым. Проблема нахождения минимального теста связана с необходимостью сокращения времени контроля.
является тестом (тривиальным тестом). Минимальный тест является тупиковым. Проблема нахождения минимального теста связана с необходимостью сокращения времени контроля.
 - множество всех наборов, на к-рых отличаются
- множество всех наборов, на к-рых отличаются  и
и  . Если в выражении
. Если в выражении  совершить умножение по правилам булевой алгебры и затем удалить "поглощаемые" члены, пользуясь соотношением
совершить умножение по правилам булевой алгебры и затем удалить "поглощаемые" члены, пользуясь соотношением  то оставшиеся произведения будут соответствовать тупиковым тестам. Так, если для рассмотренного выше примера взять задачу проверки
то оставшиеся произведения будут соответствовать тупиковым тестам. Так, если для рассмотренного выше примера взять задачу проверки 

 являются минимальными. Описанный алгоритм может быть применен для обнаружения ошибок при монтаже в соединениях элементов. Данный алгоритм с небольшими модификациями годится также для построения тупиковых кратных экспериментов для автоматов. Эффективность алгоритма построения тупиковых тестов резко падает с увеличением размеров таблицы функций неисправностей. Повышение эффективности связано с учетом строения таблицы, а также с учетом информации о структуре схемы. В этом направлении построена серия методов. Другие аспекты Н. и к. у. с. развиваются в рамках теории вероятностей.
являются минимальными. Описанный алгоритм может быть применен для обнаружения ошибок при монтаже в соединениях элементов. Данный алгоритм с небольшими модификациями годится также для построения тупиковых кратных экспериментов для автоматов. Эффективность алгоритма построения тупиковых тестов резко падает с увеличением размеров таблицы функций неисправностей. Повышение эффективности связано с учетом строения таблицы, а также с учетом информации о структуре схемы. В этом направлении построена серия методов. Другие аспекты Н. и к. у. с. развиваются в рамках теории вероятностей.