|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НАДЕЖНОСТИ ТЕОРИЯЗначение НАДЕЖНОСТИ ТЕОРИЯ в математической энциклопедии: - инженерное направление применении математич. методов, в к-ром разрабатываются: а) приемы расчета надежности технич. систем, 0) методы оценки надежности изготовленных изделий, в) способы оптимизации и повышения эффективности функционирования сложных технич. систем и составляющих их элементов в процессе эксплуатации (включая в это понятие также хранение и перевозку). В Н. т. вводятся количественные показатели надежности на основе построения соответствующих математич. моделей. При этом учитываются такие факторы, как назначение технич. системы, условия, в к-рых ей придется работать, а также экономич. факторы. В Н. т. используются разнообразные математич. методы, но особое место среди них занимают теория вероятностей и математич. статистика. Это обусловлено тем, что события, описывающие количественные и качественные показатели надежности (отказ, длительность безотказной работы, длительность ремонта, стоимость восстановления и т. п.), случайны. Широкое применение находят также методы теории оптимизации, математич. логики и др. Понятие надежности включает в себя: 1) безотказность, 2) долговечность, 3) приспособленность к ремонту. Нередко, однако, решающее значение имеет лишь первая характеристика. Так, для всех технич. устройств одноразового использования третье свойство не требуется совсем. Основным понятием Н. т. является понятие отказа, т. е. постепенной или внезапной потери устройством работоспособности. Формализованное описание этого понятия базируется на следующей общей схеме построения математич. моделей Н. т. Предполагается, что состояние технич. системы определяется точкой хв фазовом пространстве Важнейшим количественным показателем надежности является вероятность безотказной работы В Н. т. используются различные классы функций
возрастает; класс НЛС (новое лучше старого): функции распределения этого класса удовлетворяют условию
для любых
распределение Вейбулла
и др. Для увеличения надежности технич. систем используются различные приемы: резервирование, профилактич. осмотры и ремонты, эксплуатация при пониженных нагрузках. Под резервированием понимается метод повышения надежности путем введения избыточноети того или иного рода - дополнительных элементов, узлов, устройств, к-рые не требуются для функционирования технич. системы, дополнительного времени на выполнение работы, использование избыточной информации и пр. В связи с этим рассматриваются следующие типы резервирования: структурное (дополнительные элементы), временное (дополнительное время), информационное, функциональное (использующее способность элементов технич. системы выполнять дополнительные функции), нагрузочное. Структурный резерв может находиться в трех следующих состояниях: а] ненагруженном, б) нагруженном, в) облегченном. В нагруженном резерве резервный элемент несет такую же нагрузку, как и основной (рабочий), и интенсивность отказов резервного элемента та же, что у основного. В ненагруженном резерве элемент совсем не несет нагрузки, что соответствует отсутствию отказов. В облегченном резерве элемент несет нагрузку меньшую, чем основной, поэтому для него интенсивность отказов меньше, чем для основного. Значительное увеличение надежности дает восстановление отказавших элементов - резервирование с восстановлением. Если элемент имеет один резервный, находящийся в ненагруженном состоянии, функция распределения длительности безотказной работы каждого из элементов есть
где
Исследование резервированных систем явилось источником ряда чисто математич. исследований - развитие теории линейчатых и полумарковских процессов, предельных теорем для сумм случайного числа случайных величин и др. Профилактическое обслуживание применяется в моменты, когда технич. система еще работоспособна, но имеется основание считать, что появилась повышенная вероятность отказа. Обычно задачи профилактики связаны с решением вопросов оптимизации: как выбрать моменты начала профилактич. обслуживания, чтобы суммарные потери на проведение профилактики и на ущерб от возможного отказа до моментов профилактик за данный промежуток времени Тбыли минимальны; как организовать профилактич. обслуживание, чтобы вероятность безотказной работы за данный промежуток времени была максимальной и т. д. Для нек-рых функций распределения длительностей безотказной работы системы, в том числе для всех распределений класса УФИ, профилактика не увеличивает среднего времени безотказной работы. У функций распределения класса УФИ X(t)является невоз-растающей функцией. К ним, в частности, относится функция распределения
при любом постоянном Существенное место в Н. т. занимают задачи получения статистич. выводов о функции распределения наступления отказа на основе данных о результатах стендовых испытаний. Простейшие математич. модели стендовых испытаний следующие. Пусть N- число ячеек для испытаний изделий. В процессе испытаний отказавшие изделия не заменяются новыми (класс испытаний Б) или заменяются новыми (класс испытаний В). Продолжительность испытаний определяется правилом остановки, напр, заданием предельного времени испытаний Т, предельного числа rнаблюдаемых отказов и др. Существенной характеристикой испытаний является суммарная наработка Nизделий испытываются до момента
где суммарная наработка
Статистич. задачи стендовых испытаний разнообразны и требуют привлечения таких разделов математич. статистики, как теория оценивания и теория проверки статистич. гипотез. Осложняющим обстоятельством является зависимость вероятности безотказной работы от режима e проведения испытаний:
Более тяжелый режим (повышение температуры, амплитуды вибраций и т. п.) как бы приближает моменты наступления отказов. Проблема пересчета показателей надежности с одних режимов Одним из примеров оптимизации в Н. т. являются задачи оптимального резервирования. Пусть
Требуется подобрать такие числа
к-рые трактуются как ограничения на суммарный вес, объем, общую стоимость элементов и т. п. Расчет количественных показателей надежности систем с учетом возможности восстановления отказавших компонент во многом аналогичен расчету систем в массового обслуживания теории. Моментам поступления заявок в систему соответствуют моменты отказов, а длительностям обслуживания - длительности восстановления. Простейшая математич. модель соответствует процессу восстановления (см. Восстановления теория). Поскольку основные математич. модели Н. т., учитывающие восстановление отказавших элементов, не допускают явных аналитич. решений, в Н. т. интенсивно-развивается направление, связанное с использованием асимптотич. методов. При этом предполагается, что восстановление является "быстрым", т. е. заданные показатели восстановления (напр., среднее время) становятся бесконечно малыми по отношению к аналогичным показателям интервалов безотказной работы. Лит.:[1] Барзилович Е. Ю., Каштанов В. А., Некоторые математические вопросы теории обслуживания сложных систем, М., 1971: [2] Барлоу Р., Прошан Ф., Математическая теория надежности, пер. с англ., М., 1969: [3] Barlow R. E., Proschan F., Statistical theory of reliability and lifetesting: Probability models., N. Y., 1975; [4] Гнеденко Б. В., Беляев Ю. К., Соловьев А. Д., Математические методы в теории надежности, М., 1965; Е5] Коваленко И. Н., Исследования по анализу надежности сложных систем, К., 1975; [6] Козлов Б. А., Ушаков И. А., Справочник по расчету надежности аппаратуры радиоэлектроники и автоматики, М., 1975; [7] Шор Я. Б., Статистические методы анализа и контроля качества и надежности, М., 1962. Ю. К. Беляев, Б. В. Гнеденко. |
|
|
|

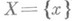 состояний. Эволюция состояний этой системы во времени описывается процессом
состояний. Эволюция состояний этой системы во времени описывается процессом 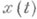 , вообще говоря, случайным. В Xвыделяется подмножество
, вообще говоря, случайным. В Xвыделяется подмножество 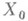 состояний, соответствующих наступлению отказа. Безотказность - свойство системы непрерывно сохранять работоспособность. Количественно безотказность измеряется временем от данного момента до момента попадания в
состояний, соответствующих наступлению отказа. Безотказность - свойство системы непрерывно сохранять работоспособность. Количественно безотказность измеряется временем от данного момента до момента попадания в  .Долговечность - свойство технич. системы сохранять работоспособность с необходимыми перерывами для ремонтов и технич. обслуживания при условии экономич. целесообразности дальнейшей эксплуатации. Ремонтоприспособленность технич. системы определяется удобством ее технич. обслуживания и проведения ремонтных работ; количественно измеряется затратами или же временем на поддержание технич. системы в работоспособном состоянии.
.Долговечность - свойство технич. системы сохранять работоспособность с необходимыми перерывами для ремонтов и технич. обслуживания при условии экономич. целесообразности дальнейшей эксплуатации. Ремонтоприспособленность технич. системы определяется удобством ее технич. обслуживания и проведения ремонтных работ; количественно измеряется затратами или же временем на поддержание технич. системы в работоспособном состоянии. технич. системы в течение времени t, т. е. вероятность того, что за время t процесс
технич. системы в течение времени t, т. е. вероятность того, что за время t процесс 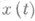 не достигнет подмножества
не достигнет подмножества 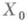 . Функция распределения наступления отказа до момента tравна
. Функция распределения наступления отказа до момента tравна  . Если существует плотность распределения
. Если существует плотность распределения  то функция
то функция  наз, функцией интенсивности отказа. Вероятностный смысл
наз, функцией интенсивности отказа. Вероятностный смысл  состоит в том, что это есть условная плотность распределения отказа при условии, что технич. система проработала безотказно время t. Таким образом,
состоит в том, что это есть условная плотность распределения отказа при условии, что технич. система проработала безотказно время t. Таким образом,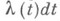 является вероятностью того, что система откажет в промежутке времени
является вероятностью того, что система откажет в промежутке времени 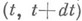 при условии, что она не отказала до момента t.
при условии, что она не отказала до момента t.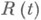 . Если
. Если 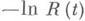 есть выпуклая функция, то функция распределения наступления отказов наз. функцией распределения с возрастающей интенсивностью отказа; класс таких функций распределения обозначается ВФИ. Если же
есть выпуклая функция, то функция распределения наступления отказов наз. функцией распределения с возрастающей интенсивностью отказа; класс таких функций распределения обозначается ВФИ. Если же 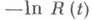 есть вогнутая функция, то функция распределения наступления отказа наз. функцией распределения с убывающей интенсивностью отказа; соответствующий класс функций распределения обозначается УФИ. В Н. т. используются и другие непара-метрич. классы функций распределения, напр, класс ВФИС (возрастающая функция интенсивности отказа в среднем): для распределений этого класса функция
есть вогнутая функция, то функция распределения наступления отказа наз. функцией распределения с убывающей интенсивностью отказа; соответствующий класс функций распределения обозначается УФИ. В Н. т. используются и другие непара-метрич. классы функций распределения, напр, класс ВФИС (возрастающая функция интенсивности отказа в среднем): для распределений этого класса функция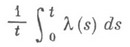
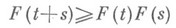
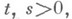 т. е. распределение отказов при условии, что технич. система уже проработала время tвыше, чем безусловное. Это и означает, что для проработавшей технич. системы отказы поступают чаще, чем для новой. Для нек-рых классов функций распределения доказаны теоремы об инвариантности функции распределения наступления отказов при образовании определенных структур (последовательного или параллельного соединения элементов и т. д.). Широкое применение в Н. т. находят модели, в к-рых функция
т. е. распределение отказов при условии, что технич. система уже проработала время tвыше, чем безусловное. Это и означает, что для проработавшей технич. системы отказы поступают чаще, чем для новой. Для нек-рых классов функций распределения доказаны теоремы об инвариантности функции распределения наступления отказов при образовании определенных структур (последовательного или параллельного соединения элементов и т. д.). Широкое применение в Н. т. находят модели, в к-рых функция 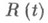 задается параметрически. В качестве функций распределения внезапных отказов часто используется экспоненциальное распределение
задается параметрически. В качестве функций распределения внезапных отказов часто используется экспоненциальное распределение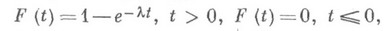
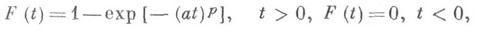
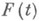 , функция распределения длительности восстановления есть
, функция распределения длительности восстановления есть 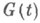 , переключатели абсолютно надежны и переключение на работу, на восстановление и в резерв происходит мгновенно, то для длительности безотказной работы дублированной системы (т. е. от начала работы до момента, когда оба элемента окажутся в состоянии отказа) имеет место формула
, переключатели абсолютно надежны и переключение на работу, на восстановление и в резерв происходит мгновенно, то для длительности безотказной работы дублированной системы (т. е. от начала работы до момента, когда оба элемента окажутся в состоянии отказа) имеет место формула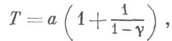

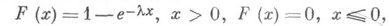
 . Ряд оптимизационных задач возникает в связи с поиском неисправностей в сложной системе: как производить поиск неисправности, чтобы затратить на ее обнаружение в среднем наименьшее время; в какой последовательности для этой цели следует проверять работоспособность составляющих систему узлов и элементов и т. д.
. Ряд оптимизационных задач возникает в связи с поиском неисправностей в сложной системе: как производить поиск неисправности, чтобы затратить на ее обнаружение в среднем наименьшее время; в какой последовательности для этой цели следует проверять работоспособность составляющих систему узлов и элементов и т. д. , т. е. сумма времен безотказной работы всех испытываемых изделий на интервале
, т. е. сумма времен безотказной работы всех испытываемых изделий на интервале  . При испытаниях по плану
. При испытаниях по плану  испытывают Nизделий, к-рые при отказах не заменяются новыми. Наблюдения продолжаются до r-го отказа. По плану
испытывают Nизделий, к-рые при отказах не заменяются новыми. Наблюдения продолжаются до r-го отказа. По плану 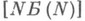 испытания продолжаются до отказа всех Nиспытываемых изделий, при использовании плана
испытания продолжаются до отказа всех Nиспытываемых изделий, при использовании плана 
 где
где  - момент отказа r-го отказавшего объекта. По моментам отказов
- момент отказа r-го отказавшего объекта. По моментам отказов  требуется проверить гипотезы о виде функции распределения наступления отказа, напр, о ее принадлежности классу ВФИ или УФИ и др.; требуется оценить ее параметры. Для оценки функции интенсивности отказа используются методы получения изотонных оценок. При испытаниях по плану
требуется проверить гипотезы о виде функции распределения наступления отказа, напр, о ее принадлежности классу ВФИ или УФИ и др.; требуется оценить ее параметры. Для оценки функции интенсивности отказа используются методы получения изотонных оценок. При испытаниях по плану 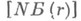 точечная несмещенная оценка параметра
точечная несмещенная оценка параметра 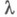 экспоненциального распределения имеет вид
экспоненциального распределения имеет вид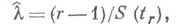
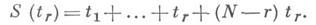
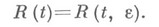
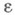 на другие
на другие 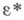 является одной из актуальных задач Н. т. Применяются планы испытаний, в к-рых режимы меняются с течением времени (примерами могут служить планы со ступенчатым нагружением). Разрабатываются математич. модели пересчета результатов ускоренных испытаний на нормальные режимы. Один из подходов к пересчету основан на гипотезе, согласно к-рой испытания в течение времени
является одной из актуальных задач Н. т. Применяются планы испытаний, в к-рых режимы меняются с течением времени (примерами могут служить планы со ступенчатым нагружением). Разрабатываются математич. модели пересчета результатов ускоренных испытаний на нормальные режимы. Один из подходов к пересчету основан на гипотезе, согласно к-рой испытания в течение времени  в режиме
в режиме 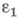 эквивалентны испытаниям в режиме
эквивалентны испытаниям в режиме  , если время
, если время  выбрано из условия
выбрано из условия 
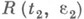 В Н. т. проводится расчет показателей функционирования систем, составленных из компонент, не являющихся абсолютно надежными. Одна из задач - оценка надежности системы по результатам стендовых испытаний компонент. Пусть система представлена в виде последовательной цепочки компонент разных типов (резервирования нет). Тогда нижняя
В Н. т. проводится расчет показателей функционирования систем, составленных из компонент, не являющихся абсолютно надежными. Одна из задач - оценка надежности системы по результатам стендовых испытаний компонент. Пусть система представлена в виде последовательной цепочки компонент разных типов (резервирования нет). Тогда нижняя  -доверительная граница вероятности безотказной работы системы
-доверительная граница вероятности безотказной работы системы 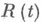 , все компоненты к-рой испытывались время
, все компоненты к-рой испытывались время  и отказы не наблюдались, совпадает с нижней
и отказы не наблюдались, совпадает с нижней 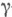 -доверительной границей вероятности безотказной работы компонент того типа, к-рые испытывались в наименьшем числе.
-доверительной границей вероятности безотказной работы компонент того типа, к-рые испытывались в наименьшем числе. - вероятности безотказной работы элементов i-го типа,
- вероятности безотказной работы элементов i-го типа,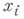 - их число. Вероятность безотказной работы системы
- их число. Вероятность безотказной работы системы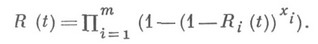
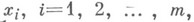 чтобы
чтобы 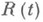 было максимальным и были выполнены неравенства
было максимальным и были выполнены неравенства