|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НАВЬЕ - СТОКСА УРАВНЕНИЯЗначение НАВЬЕ - СТОКСА УРАВНЕНИЯ в математической энциклопедии: - основные уравнения движения вязкой жидкости, представляющие математическое выражение законов сохранения импульса и массы. Для неустановившегося течения сжимаемой жидкости Н.- С. у. в декартовой системе координат могут быть, записаны в виде
где Для течений несжимаемой изотермич. жидкости (
При анализе Н.- С. у., как правило, рассматриваются в безразмерной форме, к-рая получается путем отнесения всех величин, входящих в уравнения, к соответствующим характерным величинам. Так, в случае стационарных течений несжимаемой жидкости при отсутствии массовых сил в Н.- С. у. появляется один определяющий безразмерный параметр, наз. Рейнольдса числом:
где Vи l- характерные скорости и линейный размер, v - кинематическая вязкость. Для исследования двумерных несжимаемых течений часто используются Н.- С. у. в форме Гельмгольца:
где
Основные краевые задачи для стационарных Н.- С. у. связаны с исследованием течений в замкнутых полостях, каналах, течений со свободными поверхностями, с обтеканием тел, течений в струях и следах за телами. При этом интегрирование Н.- С. у. проводится в областях (конечных или бесконечных), на границе к-рых ставятся условия из соображений физич. характера (условия прилипания или скольжения на поверхности тел, вдува или отсоса на проницаемых поверхностях, условия внешнего потока вдали от обтекаемого тела, условия на свободной границе и др.). Для нестационарных задач помимо граничных условий должны задаваться начальные условия. Строгий математич. анализ разрешимости краевых задач гидроаэромеханики для Н.- С. у. сжимаемого газа отсутствует (1982). Имеются нек-рые результаты в математич. теории динамики вязкой несжимаемой жидкости (см. Гидродинамики математические задачи). Первоначально усилия исследователей были направлены на отискание точных решений. Напр., для несжимаемой жидкости имеются точные решения для установившихся течений: в плоском канале при заданном постоянном перепаде давления (течение Пуазёйля); между двумя параллельными плоскими стенками, одна из к-рых покоится, а другая движется в своей плоскости с постоянной скоростью (течение Куэтта); в прямолинейной трубе с круглым поперечным сечением при постоянном перепаде давления (течение Хагена- Пуазейля). Найдены также нек-рые автомодельные решения, среди них: плоскопараллельное (и осесимметричное) течение вблизи критической точки (течение Хоуарта); течения в суживающемся и расширяющемся каналах (течение Гамеля). Приближенные решения Н.- С. у. основаны на упрощающих предположениях. Здесь следует отметить решения при очень малых числах Рейнольдса движениям, среди к-рых наиболее известно течение Стокса около шара. Предельный случай очень больших чисел Рейнольдса приводит к теории гидродинамического пограничного слоя. Уравнения пограничного слоя позволили решить большой круг практически важных задач на основе широко разработанных приближен ных и численных методов. Для решения нек-рых классов задач динамики вязких жидкостей и газов разработаны достаточно эффективные алгоритмы, основанные на использовании разностных схем. Напр., для задачи расчета ламинарных течений вязких несжимаемых жидкостей в областях простой формы (или около тел простой формы). Наибольшее распространение здесь получили разностные методы для уравнений в форме (3), хотя для этой системы и имеются трудности, связанные с определением граничных условий для схеме "крест", а диффузионные - по схеме Дюфорта - Франкеля. С помощью уже этих схем были получены нек-рые результаты при решении стационарных задач о ламинарных двумерных течениях в суживающемся и расширяющемся каналах, в прямоугольной выемке с движущейся крышкой, а также нестационарной задаче обтекания в канале плоской пластины, расположенной перпендикулярно к направлению потока. Неявные схемы, как правило, основаны на применении метода дробных шагов (см. [8]). Общая структура таких схем для уравнения (3) может быть представлена, напр., в виде
где
В этих формулах
где hи l- шаги сетки по хи у,
Разностные уравнения (4) обычно приводятся к трех-диагональному виду и совместно с соотношениями, аппроксимирующими граничные условия, решаются методом прогонки. При решении стационарных задач методом установления может применяться либо поочередное решение уравнений (4) (без внутренних итераций для определения Для исследования двумерных течений уравнения в форме (2) используются реже и, как правило, с некоторой регуляризацией уравнения неразрывности. Вариационно-сеточные методы, и в частности метод конечных элементов, нашли свое применение для решения уравнений динамики вязкой жидкости в форме (2) и (3). С помощью разностных методов исследовались разнообразные задачи течения вязких несжимаемых жидкостей. Среди них задачи обтекания эллиптического й кругового цилиндра (в том числе вращающегося), пластины конечной толщины (в том числе под углом атаки), ци-линдрич. торца, капли, плоской ступени и др. Изучались также течения в каверне, в плоском и Цилиндрич. канале, в канале с препятствиями на стенках, течения со свободной поверхностью, течения естественной, вынужденной и смешанной конвекции. Применение разностных методов для расчета течений вязкого сжимаемого газа на основе полных Н.- С. у. сопряжено с нек-рыми дополнительными трудностями по сравнению с расчетами течений несжимаемой вязкой жидкости. Это связано с тем, что в течениях сжимаемого газа существуют не только области пограничных слоев, но и другие области больших градиентов искомых функций, к-рые соответствуют ударным волнам и волнам разрежения в невязких течениях газа. Сложность самой системы Н.- С. у. для сжимаемого вязкого газа предъявляет повышенные требования к быстродействию и памяти ЭВМ. Использование явных схем в этом случай приводит к более простым алгоритмам. Примером явной схемы, хорошо зарекомендовавшей себя для расчета стационарных течений методом установления, является схема, к-рая для простого модельного уравнения с постоянными коэффициентами
может быть записана в виде
Эта схема аппроксимирует (5) на гладком установившемся решении с порядком Лит.:[1] Naviеr, "Mem. Acad., sci.", 1827, t. 7, p. 375-94-[2] Poisson S. D.,"J. Ecole polytechn.", 1831, t. 13, p. 1 - 174; [3] Saint-Venant, "C. r. Acact. sci.", 1843, t. 17; [4] Stоkes G. G., "Trans. Cambr. Phil. Soc", 1849, v. 8, p! 287 - 319; [5] Шлихтинг Г., Теория пограничного слоя, пер. с нем., М., 1974; [6] Том А., Эйплт К., Числовые расчеты полей в технике и физике, пер. с англ., М.- Л., 1964: [7] Браиловская И. Ю., Кускова Т. В., Чудов Л. А., в кн.: Вычислительные методы и программирование, в. 11, М., 1968, с. 3-18; [8] Яненко Н. Н., Методы дробных шагов решения многомерных задач математической физики, Новосиб., 1967; [9] Полежаев В. И., Грязнов В. Л., "Докл. АН СССР", 1974, т. 219, № 2, с. 301-04; [10] Самарский А. А., "Ж. вычисл. матем. и матем. физики", 1965, т. 5, с. 548-51; [11] КовеняВ. М., Яненко Н. Н., Метод расщепления в задачах газовой динамики, Новосиб., 1981; [12] Толстых А. И., "Ж. вычисл. матем. и матем. физики", 1978, т. 18, № 1, с. 139-53; [13] Кокошинская Н. С, Павлов Б. М., Пасконов В. М., Численное исследование сверхзвукового обтекания тел вязким газом, М., 1980; [14] Темам Р., Уравнения Навье - Стокса. Теория и численный анализ, пер. с англ., М., 1981; [15] Численное исследование современных задач газовой динамики, М., 1974; [16] Роуч П. Дж., Вычислительная гидродинамика, пер. с англ., М., 1980; [17] Rеуrеt R., Viviand H., "Lect. Notes Comput. Sci.", 1974, № 11, p. 160-84; [18] Burggral O. R., "Lect. Notes Phys.", 1976, [№ 59], p. 52-64. В. М. Пасконов. |
|
|
|


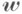 - вектор скорости с проекциями
- вектор скорости с проекциями  на соответствующие оси координат
на соответствующие оси координат  - давление,
- давление, - плотность,
- плотность, - коэффициент вязкости;
- коэффициент вязкости; - проекции вектора массовой силы
- проекции вектора массовой силы  на координатные оси;
на координатные оси; 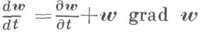 - субстанциональная производная. При выводе уравнений (1) использован обобщенный закон трения Ньютона, предполагающий, что для движущихся жидкостей и газов напряжения пропорциональны скоростям деформаций. Для исследования сжимаемых течений к уравнениям (1) необходимо добавить уравнение состояния, связывающее между собой давление, плотность и температуру, и уравнение энергии. Уравнения (1), составляющие основу гидродинамики, впервые были получены Л. Навье [1] и С. Пуассоном [2] на основе соображений о действии межмолекулярных сил. Б. Сен-Венан [3] и Дж. Г. Стоке [4] вывели эти уравнения, допуская только, что нормальные и касательные напряжения линейно связаны со скоростями деформаций.
- субстанциональная производная. При выводе уравнений (1) использован обобщенный закон трения Ньютона, предполагающий, что для движущихся жидкостей и газов напряжения пропорциональны скоростям деформаций. Для исследования сжимаемых течений к уравнениям (1) необходимо добавить уравнение состояния, связывающее между собой давление, плотность и температуру, и уравнение энергии. Уравнения (1), составляющие основу гидродинамики, впервые были получены Л. Навье [1] и С. Пуассоном [2] на основе соображений о действии межмолекулярных сил. Б. Сен-Венан [3] и Дж. Г. Стоке [4] вывели эти уравнения, допуская только, что нормальные и касательные напряжения линейно связаны со скоростями деформаций. ) уравнения (1) в векторной форме могут быть представлены в виде
) уравнения (1) в векторной форме могут быть представлены в виде


 - функция тока и
- функция тока и  - вихрь связаны с проек циями скорости
- вихрь связаны с проек циями скорости  и
и  следующим образом:
следующим образом:
 , соответствующие так наз. ползущим
, соответствующие так наз. ползущим . Первые результаты по решению стационарного варианта системы (3) были получены с помощью простейших явных пятиточечных схем и итерационных методов (см. [6]). Решение стационарных задач динамики вязкой несжимаемой жидкости большей частью основано на использовании метода установления и применении явных и неявных схем для системы (3). Среди явных схем используются двухслойные по времени схемы с симметричной аппроксимацией первых производных центральными разностями и решением второго уравнения из (3) на каждом временном слое с помощью метода Зейделя, а также трехслойная схема, в к-рой конвективные члены аппроксимируются по
. Первые результаты по решению стационарного варианта системы (3) были получены с помощью простейших явных пятиточечных схем и итерационных методов (см. [6]). Решение стационарных задач динамики вязкой несжимаемой жидкости большей частью основано на использовании метода установления и применении явных и неявных схем для системы (3). Среди явных схем используются двухслойные по времени схемы с симметричной аппроксимацией первых производных центральными разностями и решением второго уравнения из (3) на каждом временном слое с помощью метода Зейделя, а также трехслойная схема, в к-рой конвективные члены аппроксимируются по
 - разностные одномерные операторы:
- разностные одномерные операторы:
 - временной шаг,
- временной шаг, - итерационный параметр,
- итерационный параметр,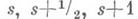 - итерационные индексы при решении уравнения Пуассона из (3) на
- итерационные индексы при решении уравнения Пуассона из (3) на  временном слое итерационным методом;
временном слое итерационным методом;
 - разностные операторы, аппроксимирующие соответствующие вторые и первые производные. Первое уравнение из (3) используется для нахождения значений
- разностные операторы, аппроксимирующие соответствующие вторые и первые производные. Первое уравнение из (3) используется для нахождения значений 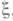 , а второе - значений
, а второе - значений  на последующем временном слое. Аппроксимация вторых производных, как правило, симметричная, а аппроксимация первых производных в уравнении для
на последующем временном слое. Аппроксимация вторых производных, как правило, симметричная, а аппроксимация первых производных в уравнении для  проводится или симметричными разностями, или односторонними разностями против потока с учетом знака скорости. Хорошо зарекомендовала себя схема в [9] с примененном монотонной аппроксимации (см. [10]). Эта схема для первого уравнения (3) имеет вид
проводится или симметричными разностями, или односторонними разностями против потока с учетом знака скорости. Хорошо зарекомендовала себя схема в [9] с примененном монотонной аппроксимации (см. [10]). Эта схема для первого уравнения (3) имеет вид

 ), либо одновременное решение соответствующих уравнений из (4) для совместного нахождения
), либо одновременное решение соответствующих уравнений из (4) для совместного нахождения 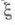 и
и 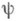 с помощью векторной прогонки. Трудности, связанные с постановкой граничных условий для уравнений (3), заключаются в том, что обычные граничные условия прилипания на твердых стенках для Н.- С. у. дают условия только для
с помощью векторной прогонки. Трудности, связанные с постановкой граничных условий для уравнений (3), заключаются в том, что обычные граничные условия прилипания на твердых стенках для Н.- С. у. дают условия только для  . Для численного решения уравнения для
. Для численного решения уравнения для 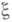 формально требуют граничные условия для вихря. Эти условия могут быть получены на каждом временном слое либо приближенно на границе области, либо путем интегрирования уравнения для
формально требуют граничные условия для вихря. Эти условия могут быть получены на каждом временном слое либо приближенно на границе области, либо путем интегрирования уравнения для  только в области, расположенной внутри основной области интегрирования [9].
только в области, расположенной внутри основной области интегрирования [9].

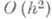 и устойчива при
и устойчива при 
 Условие устойчивости не зависит от
Условие устойчивости не зависит от  . Это означает, что при применении этой схемы к Н.- С. у. условие устойчивости не зависит от числа Рейнольдса. Тем не менее ограничение на итерационный шаг по времени для явных схем является существенным. Неявные схемы, как правило, не обладают такими ограничениями и абсолютно устойчивы для соответствующих линейных уравнений с постоянными коэффициентами. Неявные схемы для расчета двумерных течений вязкого газа используются в сочетании с методом дробных шагов. Построены (1982) различные разностные схемы метода переменных направлений: с полной и неполной аппроксимацией на промежуточных слоях, дивергентные и недивергентные (см. [11]), схемы повышенного порядка точности (выше второго) относительно шагов сетки по пространству (см. [12]). Численное моделирование течений вязкого газа на основе Н.- С. у. связано с расчетом течений сложной структуры и с использованием достаточно подробных сеток, что невозможно в силу ограниченности памяти ЭВМ без применения метода взаимно перекрывающихся областей (см. [13]). Разностные методы решения Н.- С. у. применялись для исследования большого числа задач динамики вязкого газа. Среди них задачи - сверхзвукового обтекания затупленных тел (сферы, торца кругового цилиндра), составных тел (сфера - конус, сфера - цилиндр), клина, передней кромки плоской пластины. Рассмотрены также течения в следах за телами конечных размеров, течения в соплах и воздухозаборниках, течения в полости при внешнем до- и сверхзвуковом потоке, исследовалось взаимодействие пограничного слоя с ударной волной, структура ударной волны в плазме и др. задачи. Перечисленные течения предполагались, как правило, ламинарными.
. Это означает, что при применении этой схемы к Н.- С. у. условие устойчивости не зависит от числа Рейнольдса. Тем не менее ограничение на итерационный шаг по времени для явных схем является существенным. Неявные схемы, как правило, не обладают такими ограничениями и абсолютно устойчивы для соответствующих линейных уравнений с постоянными коэффициентами. Неявные схемы для расчета двумерных течений вязкого газа используются в сочетании с методом дробных шагов. Построены (1982) различные разностные схемы метода переменных направлений: с полной и неполной аппроксимацией на промежуточных слоях, дивергентные и недивергентные (см. [11]), схемы повышенного порядка точности (выше второго) относительно шагов сетки по пространству (см. [12]). Численное моделирование течений вязкого газа на основе Н.- С. у. связано с расчетом течений сложной структуры и с использованием достаточно подробных сеток, что невозможно в силу ограниченности памяти ЭВМ без применения метода взаимно перекрывающихся областей (см. [13]). Разностные методы решения Н.- С. у. применялись для исследования большого числа задач динамики вязкого газа. Среди них задачи - сверхзвукового обтекания затупленных тел (сферы, торца кругового цилиндра), составных тел (сфера - конус, сфера - цилиндр), клина, передней кромки плоской пластины. Рассмотрены также течения в следах за телами конечных размеров, течения в соплах и воздухозаборниках, течения в полости при внешнем до- и сверхзвуковом потоке, исследовалось взаимодействие пограничного слоя с ударной волной, структура ударной волны в плазме и др. задачи. Перечисленные течения предполагались, как правило, ламинарными.