"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МОЩНОСТНАЯ ХАРАКТЕРИСТИКА
Значение МОЩНОСТНАЯ ХАРАКТЕРИСТИКА в математической энциклопедии:
топологического пространства - функция, сопоставляющая этому пространству бесконечное кардинальное число и принимающая одинаковые значения на гомеоморфных пространствах. М. х. наз. также кардинальными инвариантами. Областью определения М. х. может служить класс всех тополо-гич. пространств или нек-рый его подкласс. Следующие М. х. были выделены уже на первом этапе развития общей топологии. Пусть X- произвольное топологич. пространство. Его мощность  есть мощность множества всех его точек - тривиальный инвариант. Вес
есть мощность множества всех его точек - тривиальный инвариант. Вес  - минимум мощностей всевозможных баз пространства X. Плотность
- минимум мощностей всевозможных баз пространства X. Плотность  - минимум мощностей всюду плотных в Xмножеств. Число Суслина
- минимум мощностей всюду плотных в Xмножеств. Число Суслина  - наименьший бесконечный кардинал т такой, что мощность всякого семейства попарно не пересекающихся непустых открытых множеств в X не превосходит
- наименьший бесконечный кардинал т такой, что мощность всякого семейства попарно не пересекающихся непустых открытых множеств в X не превосходит  .ЧислоЛинделёфа
.ЧислоЛинделёфа  - наименьший бесконечный кардинал
- наименьший бесконечный кардинал  такой, что из всякого-открытого покрытия пространства Xможно выделить подпокрытие мощности
такой, что из всякого-открытого покрытия пространства Xможно выделить подпокрытие мощности  . Эти простые понятия сразу доказали свою важность, войдя решающим образом в формулировки фундаментальных теорем и проблем. Примеры: регулярное пространство счетного веса метризуемо (теорема Урысона - Тихонова, 1925), бикомпакт метризуем в том и только в том случае, если вес его счетен; для пространства X любой бикомпактной группы число Суслина счетно; число Линделёфа
. Эти простые понятия сразу доказали свою важность, войдя решающим образом в формулировки фундаментальных теорем и проблем. Примеры: регулярное пространство счетного веса метризуемо (теорема Урысона - Тихонова, 1925), бикомпакт метризуем в том и только в том случае, если вес его счетен; для пространства X любой бикомпактной группы число Суслина счетно; число Линделёфа  счетно (т. е. равно
счетно (т. е. равно  ) для всякого пространства X счетного веса. Проблема Суслина: верно ли, что всякий связный упорядоченный бикомпакт X такой, что
) для всякого пространства X счетного веса. Проблема Суслина: верно ли, что всякий связный упорядоченный бикомпакт X такой, что  гомеоморфен обычному отрезку [0, 1], сводится к вопросу о соотношении между двумя М. х.: плотностью и числом Суслина. Для положительного решения проблемы Суслина достаточно-в указанных выше предположениях установить, что-
гомеоморфен обычному отрезку [0, 1], сводится к вопросу о соотношении между двумя М. х.: плотностью и числом Суслина. Для положительного решения проблемы Суслина достаточно-в указанных выше предположениях установить, что- . Вопрос о сравнении М. х. между собой - решение к-рого, как видно из приведенного примера, может иметь ключевое значение для окончательного заключения о строении пространства - занимает центральное место в теории М. х. Причина этому находится в самой природе понятия М. х.: значениями М. х. являются кардинальные числа, совокупность к-рых вполне упорядочена по величине. Следовательно, любые две М. х.
. Вопрос о сравнении М. х. между собой - решение к-рого, как видно из приведенного примера, может иметь ключевое значение для окончательного заключения о строении пространства - занимает центральное место в теории М. х. Причина этому находится в самой природе понятия М. х.: значениями М. х. являются кардинальные числа, совокупность к-рых вполне упорядочена по величине. Следовательно, любые две М. х. можно пытаться сравнить по величине. Возникает серия взаимосвязанных вопросов. Верно ли, что для любого
можно пытаться сравнить по величине. Возникает серия взаимосвязанных вопросов. Верно ли, что для любого  для каких
для каких 
 , когда
, когда  и т. д.
и т. д.
С кардинальными числами можно производить вычисления: перемножать их, складывать, возводить в степень. Соответственно, можно производить вычисления и с кардинальными инвариантами - перемножать и складывать их как функции и т. д. Это открывает новые возможности для сравнения М. х.- с помощью вычислений. Всегда

- т. е. число Суслина не превосходит плотности, плотность не превосходит веса и число Линделёфа не препосходит веса. Но плотность и число Линделёфа в этом смысле не сравнимы: существуют пространства X, Y, Z, для к-рых

Неожиданной на первый взгляд представляется несравнимость мощности и веса: существуют нормальные счетные  -пространства несчетного веса. Но всегда
-пространства несчетного веса. Но всегда 
 и
и  . Для всякого
. Для всякого  -пространства X,
-пространства X, (пишут ехр
(пишут ехр  вместо
вместо  ). Для всякого хаусдорфова пространства
). Для всякого хаусдорфова пространства  Всегда
Всегда  . .
. .
В задачу сравнения могут быть естественно вовлечены не два, а большее число М. х. На этом пути получаются особенно тонкие, красивые и часто неожиданные результаты, поражающие своей общностью: для каждого хаусдорфова пространства  где
где  - наименьший бесконечный кардинал
- наименьший бесконечный кардинал  такой, что в каждой точке пространства
такой, что в каждой точке пространства  имеется база мощности
имеется база мощности  (см. [1], [2]). Исследования в теории М. х. стимулировала проблема оценки мощности бикомпакта с первой аксиомой счетности, остававшаяся нерешенной с 1923 по 1969. Оказалось: для каждого хаусдорфова пространства
(см. [1], [2]). Исследования в теории М. х. стимулировала проблема оценки мощности бикомпакта с первой аксиомой счетности, остававшаяся нерешенной с 1923 по 1969. Оказалось: для каждого хаусдорфова пространства  (теорема Архангельского, см. [2], [4]).
(теорема Архангельского, см. [2], [4]).
Вычисления М. х. возникают во всех разделах общей топологии в силу теоретико-множественной природы последней. Поэтому и применения теория М. х. находит практически во всех областях общей топологии и при любых подходах к исследованию пространств.
В частности, при изучении пространств методом покрытий на первый план выступают число Линделёфа, плотность и число Суслина. При исследовании и классификации пространств методом непрерывных отображений (в частности, при построении теории диадич. бикомпактов и теории абсолютов) возникли и сыграли ключевую роль новые М. х.: спрэд и  -вес. Спрэд
-вес. Спрэд  пространства Xесть точная верхняя грань мощностей дискретных подпространств пространства X, а
пространства Xесть точная верхняя грань мощностей дискретных подпространств пространства X, а  -вес
-вес  этого пространства - минимум мощностей всевозможных семейств
этого пространства - минимум мощностей всевозможных семейств  (наз.
(наз.  -базами) непустых открытых в Xмножеств таких, что для каждого непустого открытого в Xмножества Uнайдется
-базами) непустых открытых в Xмножеств таких, что для каждого непустого открытого в Xмножества Uнайдется  такое, что
такое, что  . При исследовании пространств методом обратных спектров важную роль играют число Суслина, характер, вес. Но имеется подход к общей топологии, при к-ром М. х. выступают и как главное средство исследования строения пространств, и как основной язык, на к-ром выражаются свойства пространств из тех или иных классов и, наконец, как средство классификации и выделения новых естественных классов топологич. пространств. В основе и здесь лежит задача сравнения M, х. Основной вопрос ставится следующим образом. Дан класс
. При исследовании пространств методом обратных спектров важную роль играют число Суслина, характер, вес. Но имеется подход к общей топологии, при к-ром М. х. выступают и как главное средство исследования строения пространств, и как основной язык, на к-ром выражаются свойства пространств из тех или иных классов и, наконец, как средство классификации и выделения новых естественных классов топологич. пространств. В основе и здесь лежит задача сравнения M, х. Основной вопрос ставится следующим образом. Дан класс  тоиологич. пространств, к-рым ограничивается область определения М. х. Как выглядят основные соотношения между кардинальными инвариантами в этих условиях? Развивая теорию М. х. для класса
тоиологич. пространств, к-рым ограничивается область определения М. х. Как выглядят основные соотношения между кардинальными инвариантами в этих условиях? Развивая теорию М. х. для класса  , мы как бы получаем "кардинальный портрет" класса
, мы как бы получаем "кардинальный портрет" класса  . Сравнение кардинальных портретов каких-либо классов
. Сравнение кардинальных портретов каких-либо классов  дает возможность судить
дает возможность судить
о соотношениях между этими классами, а также доставляет эффективные средства доказательства для конкретных пространств принадлежности их тому или иному классу.
Этот подход демонстрируется на примере класса метризуемых пространств. Характерной чертой здесь является совпадение для этого класса ряда основных М. х.: число Суслина равно плотности, весу и числу Линделёфа. Этот факт часто применяется, напр, чтобы доказать, что нек-рое пространство неметризуемо, достаточно показать, что на нем различаются хотя бы два из названных выше инвариантов.
Если в классе метризуемых пространств теория М. х. отличается главным образом упрощениями, то в классе бикомпактов она совершенно и нетривиальным образом меняет свой вид. Ответственны за это фундаментальные положения этой теории - совпадение для бикомпактов характера и псевдохарактера, веса и сетевого веса. При этом псевдохарактером  пространства Xв точке хназ. наименьшее число открытых множеств, дающих эту точку в пересечении, а характером
пространства Xв точке хназ. наименьшее число открытых множеств, дающих эту точку в пересечении, а характером  пространства Xв точке хназ. минимум мощностей баз пространства в этой точке. Сетевым весом
пространства Xв точке хназ. минимум мощностей баз пространства в этой точке. Сетевым весом  наз. минимум мощностей семейств
наз. минимум мощностей семейств  множеств в X, удовлетворяющих условию: если
множеств в X, удовлетворяющих условию: если  и
и  где Uоткрыто в X, то найдется
где Uоткрыто в X, то найдется  , для к-рого
, для к-рого  (такие семейства наз. сетями в X). Для всякого бикомпакта Xверно следующее: 1)
(такие семейства наз. сетями в X). Для всякого бикомпакта Xверно следующее: 1)  для всех
для всех  2)
2)
Поэтому при непрерывном отображении на бикомпакт вес не может возрастать, и если бикомпакт Xпредставлен в виде объединения двух своих подпространств  и
и  , то вес
, то вес  не превосходит максимума весов
не превосходит максимума весов  и
и  (аддиционная теорема для веса). По той же причине вес бикомпакта всегда не превосходит его мощности - в частности, всякий счетный бикомпакт метризуем. Ни одно из перечисленных выше положений теории М. х. в классе бикомпактов не распространяется на класс всех вполне регулярных пространств. Важным специфич. результатом является следующий: если
(аддиционная теорема для веса). По той же причине вес бикомпакта всегда не превосходит его мощности - в частности, всякий счетный бикомпакт метризуем. Ни одно из перечисленных выше положений теории М. х. в классе бикомпактов не распространяется на класс всех вполне регулярных пространств. Важным специфич. результатом является следующий: если  - бикомпакт,
- бикомпакт, - кардинал,
- кардинал, и
и  для всех
для всех  , то
, то  (теорема Чеха - Поспишила). Почти все критерии метризуемости бикомпактов также являются теоремами о М. х. Так, метризуемость бикомпакта Xравносильна любому из следующих условий: а)
(теорема Чеха - Поспишила). Почти все критерии метризуемости бикомпактов также являются теоремами о М. х. Так, метризуемость бикомпакта Xравносильна любому из следующих условий: а) б)
б) в) диагональ в
в) диагональ в  является множеством типа
является множеством типа  ; г) Xобладает точечно-счетной базой.
; г) Xобладает точечно-счетной базой.
В исследовании строения бикомпактов важная роль принадлежит тесноте. Теснотой  (см. [2], [4]) пространства X наз. наименьший кардинал
(см. [2], [4]) пространства X наз. наименьший кардинал  такой, что если
такой, что если  то найдется
то найдется  , для к-рого
, для к-рого  Теснота не возрастает при возведении бикомпакта в любую конечную степень (в классе вполне регулярных пространств это - не так).
Теснота не возрастает при возведении бикомпакта в любую конечную степень (в классе вполне регулярных пространств это - не так).
Если теснота бикомпакта  не превосходит
не превосходит  , то для каждой точки
, то для каждой точки  найдется семейство
найдется семейство  непустых открытых в Xмножеств такое, что
непустых открытых в Xмножеств такое, что 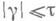 и каждая окрестность
и каждая окрестность  точки
точки  содержит элемент семейства
содержит элемент семейства  Поэтому л-вес каждого сепарабельного бикомпакта счетной тесноты равен
Поэтому л-вес каждого сепарабельного бикомпакта счетной тесноты равен  Спрэд бикомпакта мажорирует его тесноту.
Спрэд бикомпакта мажорирует его тесноту.
Особыми свойствами диадич. бикомпактов также в большой степени управляют теоремы о М. х. Так, для всякого диадич. бикомпакта его вес совпадает со спрэ-дом и с теснотой. К числу диадич. бикомпактов относятся пространства любых бикомпактных групп, так что, в частности, каждая бикомпактная группа счетной тесноты метризуема.
Для теории диадич. бикомпактов и других разделов теории М. х. важное значение имеет вопрос о поведении последних при операции умножения. Существенную роль играют здесь следующие две теоремы, первая из к-рых влечет вторую. Если F- семейство пространства такое, что  для каждого
для каждого  и
и  то плотность произведения всех пространств из Fне превосходит
то плотность произведения всех пространств из Fне превосходит  (см. [1]- [4]). Если X - произведение какого-нибудь множества пространств, плотность каждого из к-рых не превосходит
(см. [1]- [4]). Если X - произведение какого-нибудь множества пространств, плотность каждого из к-рых не превосходит  , то
, то  . В последнем утверждении нет никаких ограничений на число сомножителей. В частности, получается, что число Суслина любого тихоновского куба (произведения произвольного множества отрезков) счетно. Таким образом, условие
. В последнем утверждении нет никаких ограничений на число сомножителей. В частности, получается, что число Суслина любого тихоновского куба (произведения произвольного множества отрезков) счетно. Таким образом, условие  не несет в себе ограничения на мощность пространства.
не несет в себе ограничения на мощность пространства.
Многие просто формулируемые вопросы о поведении М. х. при операции умножения оказываются весьма деликатными. Например, верно ли, что всегда  оказывается связанным с гипотезой Суслина и континуум-гипотезой?
оказывается связанным с гипотезой Суслина и континуум-гипотезой?
Напротив, поведение М. х. при переходе от пространства Xк его образу Y при непрерывном отображении  подчиняется в основном простым общим правилам.
подчиняется в основном простым общим правилам.
Напр., всегда 
 Если f факторно, то
Если f факторно, то  . То обстоятельство, что основу теории М. х. составляет система простых универсальных правил этого рода, 'также можно рассматривать как одну из причин, обеспечивающих широкую применимость этой теории.
. То обстоятельство, что основу теории М. х. составляет система простых универсальных правил этого рода, 'также можно рассматривать как одну из причин, обеспечивающих широкую применимость этой теории.
Значительная информация о строении пространств получается при рассмотрении вопроса: как ведут себя М. х. при переходе к подпространству. Те М. х.  , для к-рых из
, для к-рых из  всегда следует, что
всегда следует, что  наз. монотонными. К ним относятся: вес, сетевой вес, теснота, характер, спрэд. Немонотонны число Суслина, плотность, число Линделёфа. Возникают следующие вопросы: каковы те пространства X, для к-рых
наз. монотонными. К ним относятся: вес, сетевой вес, теснота, характер, спрэд. Немонотонны число Суслина, плотность, число Линделёфа. Возникают следующие вопросы: каковы те пространства X, для к-рых  для всех
для всех  ; каковы те
; каковы те  , для к-рых
, для к-рых  для всех
для всех  ; как отражается на топологии пространства X требование:
; как отражается на топологии пространства X требование: для всех
для всех  . Ответ на первый вопрос прост: сформулированное условие означает, что спрэд Xне превосходит
. Ответ на первый вопрос прост: сформулированное условие означает, что спрэд Xне превосходит  . Но двумя последующими требованиями выделяются новые классы пространств. Исследование их оказалось зависящим от специальных гипотез теории множеств - в частности, от аксиомы Мартина.
. Но двумя последующими требованиями выделяются новые классы пространств. Исследование их оказалось зависящим от специальных гипотез теории множеств - в частности, от аксиомы Мартина.
Своеобразный характер приобретает теория М. х. на пространствах топология, групп. Так, критерий метризуемости сводится здесь просто к требованию счет-ностн характера. На языке М. х. формулируются важные свойства линейных топологич. пространств, в частности пространств  непрерывных действительных функций на пространстве X. Сюда относятся теоремы о бикомпактах Эберлейна (каждый бикомпакт Эберлейна является пространством Фреше - Урысона, вес бикомпакта Эберлейна равен его числу Суслина), теорема: если X- бикомпакт, то теснота пространства С(X)в топологии поточечной сходимости счетна.
непрерывных действительных функций на пространстве X. Сюда относятся теоремы о бикомпактах Эберлейна (каждый бикомпакт Эберлейна является пространством Фреше - Урысона, вес бикомпакта Эберлейна равен его числу Суслина), теорема: если X- бикомпакт, то теснота пространства С(X)в топологии поточечной сходимости счетна.
Между рядом М. х. пространств Xи С(X)имеет место соответствие типа двойственности.
Лит.:[1] JuhaszI., Cardinal functions in topology, Amst., 1971; [2] Архангельский А. В., Пономарев В. И., Основы общей топологии в задачах и упражнениях, М., 1974; [3] Engelking R., General topology, Warsz., 1977; [4] Архангельский А. В., "Успехи матем. наук", 1978, т. 33, в. 6, с. 29-84; [5] Еngelking R., General topology, Warsz., 1977.
А. В. Архангельский.

 есть мощность множества всех его точек - тривиальный инвариант. Вес
есть мощность множества всех его точек - тривиальный инвариант. Вес  - минимум мощностей всевозможных баз пространства X. Плотность
- минимум мощностей всевозможных баз пространства X. Плотность  - минимум мощностей всюду плотных в Xмножеств. Число Суслина
- минимум мощностей всюду плотных в Xмножеств. Число Суслина  - наименьший бесконечный кардинал т такой, что мощность всякого семейства попарно не пересекающихся непустых открытых множеств в X не превосходит
- наименьший бесконечный кардинал т такой, что мощность всякого семейства попарно не пересекающихся непустых открытых множеств в X не превосходит  .ЧислоЛинделёфа
.ЧислоЛинделёфа  - наименьший бесконечный кардинал
- наименьший бесконечный кардинал  такой, что из всякого-открытого покрытия пространства Xможно выделить подпокрытие мощности
такой, что из всякого-открытого покрытия пространства Xможно выделить подпокрытие мощности  . Эти простые понятия сразу доказали свою важность, войдя решающим образом в формулировки фундаментальных теорем и проблем. Примеры: регулярное пространство счетного веса метризуемо (теорема Урысона - Тихонова, 1925), бикомпакт метризуем в том и только в том случае, если вес его счетен; для пространства X любой бикомпактной группы число Суслина счетно; число Линделёфа
. Эти простые понятия сразу доказали свою важность, войдя решающим образом в формулировки фундаментальных теорем и проблем. Примеры: регулярное пространство счетного веса метризуемо (теорема Урысона - Тихонова, 1925), бикомпакт метризуем в том и только в том случае, если вес его счетен; для пространства X любой бикомпактной группы число Суслина счетно; число Линделёфа  счетно (т. е. равно
счетно (т. е. равно  ) для всякого пространства X счетного веса. Проблема Суслина: верно ли, что всякий связный упорядоченный бикомпакт X такой, что
) для всякого пространства X счетного веса. Проблема Суслина: верно ли, что всякий связный упорядоченный бикомпакт X такой, что  гомеоморфен обычному отрезку [0, 1], сводится к вопросу о соотношении между двумя М. х.: плотностью и числом Суслина. Для положительного решения проблемы Суслина достаточно-в указанных выше предположениях установить, что-
гомеоморфен обычному отрезку [0, 1], сводится к вопросу о соотношении между двумя М. х.: плотностью и числом Суслина. Для положительного решения проблемы Суслина достаточно-в указанных выше предположениях установить, что- . Вопрос о сравнении М. х. между собой - решение к-рого, как видно из приведенного примера, может иметь ключевое значение для окончательного заключения о строении пространства - занимает центральное место в теории М. х. Причина этому находится в самой природе понятия М. х.: значениями М. х. являются кардинальные числа, совокупность к-рых вполне упорядочена по величине. Следовательно, любые две М. х.
. Вопрос о сравнении М. х. между собой - решение к-рого, как видно из приведенного примера, может иметь ключевое значение для окончательного заключения о строении пространства - занимает центральное место в теории М. х. Причина этому находится в самой природе понятия М. х.: значениями М. х. являются кардинальные числа, совокупность к-рых вполне упорядочена по величине. Следовательно, любые две М. х. можно пытаться сравнить по величине. Возникает серия взаимосвязанных вопросов. Верно ли, что для любого
можно пытаться сравнить по величине. Возникает серия взаимосвязанных вопросов. Верно ли, что для любого  для каких
для каких 
 , когда
, когда  и т. д.
и т. д.

 -пространства несчетного веса. Но всегда
-пространства несчетного веса. Но всегда 
 и
и  . Для всякого
. Для всякого  -пространства X,
-пространства X, (пишут ехр
(пишут ехр  вместо
вместо  ). Для всякого хаусдорфова пространства
). Для всякого хаусдорфова пространства  Всегда
Всегда  . .
. . где
где  - наименьший бесконечный кардинал
- наименьший бесконечный кардинал  такой, что в каждой точке пространства
такой, что в каждой точке пространства  имеется база мощности
имеется база мощности  (см. [1], [2]). Исследования в теории М. х. стимулировала проблема оценки мощности бикомпакта с первой аксиомой счетности, остававшаяся нерешенной с 1923 по 1969. Оказалось: для каждого хаусдорфова пространства
(см. [1], [2]). Исследования в теории М. х. стимулировала проблема оценки мощности бикомпакта с первой аксиомой счетности, остававшаяся нерешенной с 1923 по 1969. Оказалось: для каждого хаусдорфова пространства  (теорема Архангельского, см. [2], [4]).
(теорема Архангельского, см. [2], [4]). -вес. Спрэд
-вес. Спрэд  пространства Xесть точная верхняя грань мощностей дискретных подпространств пространства X, а
пространства Xесть точная верхняя грань мощностей дискретных подпространств пространства X, а  -вес
-вес  этого пространства - минимум мощностей всевозможных семейств
этого пространства - минимум мощностей всевозможных семейств  (наз.
(наз.  -базами) непустых открытых в Xмножеств таких, что для каждого непустого открытого в Xмножества Uнайдется
-базами) непустых открытых в Xмножеств таких, что для каждого непустого открытого в Xмножества Uнайдется  такое, что
такое, что  . При исследовании пространств методом обратных спектров важную роль играют число Суслина, характер, вес. Но имеется подход к общей топологии, при к-ром М. х. выступают и как главное средство исследования строения пространств, и как основной язык, на к-ром выражаются свойства пространств из тех или иных классов и, наконец, как средство классификации и выделения новых естественных классов топологич. пространств. В основе и здесь лежит задача сравнения M, х. Основной вопрос ставится следующим образом. Дан класс
. При исследовании пространств методом обратных спектров важную роль играют число Суслина, характер, вес. Но имеется подход к общей топологии, при к-ром М. х. выступают и как главное средство исследования строения пространств, и как основной язык, на к-ром выражаются свойства пространств из тех или иных классов и, наконец, как средство классификации и выделения новых естественных классов топологич. пространств. В основе и здесь лежит задача сравнения M, х. Основной вопрос ставится следующим образом. Дан класс  тоиологич. пространств, к-рым ограничивается область определения М. х. Как выглядят основные соотношения между кардинальными инвариантами в этих условиях? Развивая теорию М. х. для класса
тоиологич. пространств, к-рым ограничивается область определения М. х. Как выглядят основные соотношения между кардинальными инвариантами в этих условиях? Развивая теорию М. х. для класса  , мы как бы получаем "кардинальный портрет" класса
, мы как бы получаем "кардинальный портрет" класса  . Сравнение кардинальных портретов каких-либо классов
. Сравнение кардинальных портретов каких-либо классов  дает возможность судить
дает возможность судить пространства Xв точке хназ. наименьшее число открытых множеств, дающих эту точку в пересечении, а характером
пространства Xв точке хназ. наименьшее число открытых множеств, дающих эту точку в пересечении, а характером  пространства Xв точке хназ. минимум мощностей баз пространства в этой точке. Сетевым весом
пространства Xв точке хназ. минимум мощностей баз пространства в этой точке. Сетевым весом  наз. минимум мощностей семейств
наз. минимум мощностей семейств  множеств в X, удовлетворяющих условию: если
множеств в X, удовлетворяющих условию: если  и
и  где Uоткрыто в X, то найдется
где Uоткрыто в X, то найдется  , для к-рого
, для к-рого  (такие семейства наз. сетями в X). Для всякого бикомпакта Xверно следующее: 1)
(такие семейства наз. сетями в X). Для всякого бикомпакта Xверно следующее: 1)  для всех
для всех  2)
2)
 и
и  , то вес
, то вес  не превосходит максимума весов
не превосходит максимума весов  и
и  (аддиционная теорема для веса). По той же причине вес бикомпакта всегда не превосходит его мощности - в частности, всякий счетный бикомпакт метризуем. Ни одно из перечисленных выше положений теории М. х. в классе бикомпактов не распространяется на класс всех вполне регулярных пространств. Важным специфич. результатом является следующий: если
(аддиционная теорема для веса). По той же причине вес бикомпакта всегда не превосходит его мощности - в частности, всякий счетный бикомпакт метризуем. Ни одно из перечисленных выше положений теории М. х. в классе бикомпактов не распространяется на класс всех вполне регулярных пространств. Важным специфич. результатом является следующий: если  - бикомпакт,
- бикомпакт, - кардинал,
- кардинал, и
и  для всех
для всех  , то
, то  (теорема Чеха - Поспишила). Почти все критерии метризуемости бикомпактов также являются теоремами о М. х. Так, метризуемость бикомпакта Xравносильна любому из следующих условий: а)
(теорема Чеха - Поспишила). Почти все критерии метризуемости бикомпактов также являются теоремами о М. х. Так, метризуемость бикомпакта Xравносильна любому из следующих условий: а) б)
б) в) диагональ в
в) диагональ в  является множеством типа
является множеством типа  ; г) Xобладает точечно-счетной базой.
; г) Xобладает точечно-счетной базой. (см. [2], [4]) пространства X наз. наименьший кардинал
(см. [2], [4]) пространства X наз. наименьший кардинал  такой, что если
такой, что если  то найдется
то найдется  , для к-рого
, для к-рого  Теснота не возрастает при возведении бикомпакта в любую конечную степень (в классе вполне регулярных пространств это - не так).
Теснота не возрастает при возведении бикомпакта в любую конечную степень (в классе вполне регулярных пространств это - не так). не превосходит
не превосходит  , то для каждой точки
, то для каждой точки  найдется семейство
найдется семейство  непустых открытых в Xмножеств такое, что
непустых открытых в Xмножеств такое, что 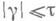 и каждая окрестность
и каждая окрестность  точки
точки  содержит элемент семейства
содержит элемент семейства  Поэтому л-вес каждого сепарабельного бикомпакта счетной тесноты равен
Поэтому л-вес каждого сепарабельного бикомпакта счетной тесноты равен  Спрэд бикомпакта мажорирует его тесноту.
Спрэд бикомпакта мажорирует его тесноту. для каждого
для каждого  и
и  то плотность произведения всех пространств из Fне превосходит
то плотность произведения всех пространств из Fне превосходит  (см. [1]- [4]). Если X - произведение какого-нибудь множества пространств, плотность каждого из к-рых не превосходит
(см. [1]- [4]). Если X - произведение какого-нибудь множества пространств, плотность каждого из к-рых не превосходит  , то
, то  . В последнем утверждении нет никаких ограничений на число сомножителей. В частности, получается, что число Суслина любого тихоновского куба (произведения произвольного множества отрезков) счетно. Таким образом, условие
. В последнем утверждении нет никаких ограничений на число сомножителей. В частности, получается, что число Суслина любого тихоновского куба (произведения произвольного множества отрезков) счетно. Таким образом, условие  не несет в себе ограничения на мощность пространства.
не несет в себе ограничения на мощность пространства. оказывается связанным с гипотезой Суслина и континуум-гипотезой?
оказывается связанным с гипотезой Суслина и континуум-гипотезой? подчиняется в основном простым общим правилам.
подчиняется в основном простым общим правилам.
 Если f факторно, то
Если f факторно, то  . То обстоятельство, что основу теории М. х. составляет система простых универсальных правил этого рода, 'также можно рассматривать как одну из причин, обеспечивающих широкую применимость этой теории.
. То обстоятельство, что основу теории М. х. составляет система простых универсальных правил этого рода, 'также можно рассматривать как одну из причин, обеспечивающих широкую применимость этой теории. , для к-рых из
, для к-рых из  всегда следует, что
всегда следует, что  наз. монотонными. К ним относятся: вес, сетевой вес, теснота, характер, спрэд. Немонотонны число Суслина, плотность, число Линделёфа. Возникают следующие вопросы: каковы те пространства X, для к-рых
наз. монотонными. К ним относятся: вес, сетевой вес, теснота, характер, спрэд. Немонотонны число Суслина, плотность, число Линделёфа. Возникают следующие вопросы: каковы те пространства X, для к-рых  для всех
для всех  ; каковы те
; каковы те  , для к-рых
, для к-рых  для всех
для всех  ; как отражается на топологии пространства X требование:
; как отражается на топологии пространства X требование: для всех
для всех  . Ответ на первый вопрос прост: сформулированное условие означает, что спрэд Xне превосходит
. Ответ на первый вопрос прост: сформулированное условие означает, что спрэд Xне превосходит  . Но двумя последующими требованиями выделяются новые классы пространств. Исследование их оказалось зависящим от специальных гипотез теории множеств - в частности, от аксиомы Мартина.
. Но двумя последующими требованиями выделяются новые классы пространств. Исследование их оказалось зависящим от специальных гипотез теории множеств - в частности, от аксиомы Мартина. непрерывных действительных функций на пространстве X. Сюда относятся теоремы о бикомпактах Эберлейна (каждый бикомпакт Эберлейна является пространством Фреше - Урысона, вес бикомпакта Эберлейна равен его числу Суслина), теорема: если X- бикомпакт, то теснота пространства С(X)в топологии поточечной сходимости счетна.
непрерывных действительных функций на пространстве X. Сюда относятся теоремы о бикомпактах Эберлейна (каждый бикомпакт Эберлейна является пространством Фреше - Урысона, вес бикомпакта Эберлейна равен его числу Суслина), теорема: если X- бикомпакт, то теснота пространства С(X)в топологии поточечной сходимости счетна.