"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МОРСА НЕРАВЕНСТВА
Значение МОРСА НЕРАВЕНСТВА в математической энциклопедии:
- вытекающие из теории Морса неравенства, связывающие число критических точек функции Морса на многообразии с его гомологич. инвариантами.
Пусть f - Морса функция на гладком n-мерном многообразии (без края) М, имеющая конечное число критич. точек. Тогда гомологии группы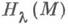 конечно порождены и потому определены их ранги
конечно порождены и потому определены их ранги 
 и периодич. ранги
и периодич. ранги  (периодический ранг абелевой группы Ас конечным числом образующих - минимальное число циклич. групп, в прямую сумму к-рых может быть разложена максимальная периодич. подгруппа группы А). М. н. связывают число
(периодический ранг абелевой группы Ас конечным числом образующих - минимальное число циклич. групп, в прямую сумму к-рых может быть разложена максимальная периодич. подгруппа группы А). М. н. связывают число  критич. точек функции
критич. точек функции  , имеющих Морса индекс
, имеющих Морса индекс , с этими рангами, и имеют вид:
, с этими рангами, и имеют вид:
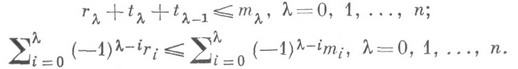
При  последнее М. н. всегда является равенством, так что
последнее М. н. всегда является равенством, так что

где 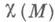 - эйлерова характеристика многообразия М.
- эйлерова характеристика многообразия М.
М. н. имеют место и для функций Морса триад 
 достаточно заменить группы
достаточно заменить группы 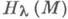 группами относительных гомологии
группами относительных гомологии  .
.
Согласно М. н. многообразие, имеющее "большие" группы гомологии, не допускает функций Морса с малым числом критич. точек. Замечательно, что даваемые М. н. оценки точны: на замкнутом односвязном многообразии размерности  существует функция Морса, для к-рой М. н. являются равенствами (Смейла теорема, см. [2]). В частности, на любом замкнутом многообразии, гомотопически эквивалентном сфере
существует функция Морса, для к-рой М. н. являются равенствами (Смейла теорема, см. [2]). В частности, на любом замкнутом многообразии, гомотопически эквивалентном сфере  , существует функция Морса с двумя критич. точками, откуда непосредственно следует (см. Морса теория), что многообразие Мгомеоморфно сфере
, существует функция Морса с двумя критич. точками, откуда непосредственно следует (см. Морса теория), что многообразие Мгомеоморфно сфере  (см. Пуанкаре гипотеза). Аналогичное применение теоремы Смейла позволяет доказать и теоремы об h- и s-кобордизмах.
(см. Пуанкаре гипотеза). Аналогичное применение теоремы Смейла позволяет доказать и теоремы об h- и s-кобордизмах.
Аналоги М. н. имеют место также для функций Морса 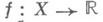 на бесконечномерных гильбертовых многообразиях и связывают (для любых регулярных значений
на бесконечномерных гильбертовых многообразиях и связывают (для любых регулярных значений 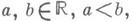 функции f) числа
функции f) числа  лежащих в
лежащих в  критич. точек конечного индекса
критич. точек конечного индекса  с рангом
с рангом  и периодич. рангом
и периодич. рангом  группы
группы  где
где  . Именно,
. Именно,
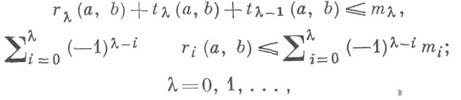
При достаточно больших  последнее неравенство становится равенством.
последнее неравенство становится равенством.
Лит.:[l] Morse M., The calculus of variations in the large, N. Y., 1934; [2] Смейл С, "Математика", 1964, т. 8, № 4, с. 95-108.
М. М. Постников, Ю. В. Рудяк.

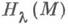 конечно порождены и потому определены их ранги
конечно порождены и потому определены их ранги 
 и периодич. ранги
и периодич. ранги  (периодический ранг абелевой группы Ас конечным числом образующих - минимальное число циклич. групп, в прямую сумму к-рых может быть разложена максимальная периодич. подгруппа группы А). М. н. связывают число
(периодический ранг абелевой группы Ас конечным числом образующих - минимальное число циклич. групп, в прямую сумму к-рых может быть разложена максимальная периодич. подгруппа группы А). М. н. связывают число  критич. точек функции
критич. точек функции  , имеющих Морса индекс
, имеющих Морса индекс , с этими рангами, и имеют вид:
, с этими рангами, и имеют вид: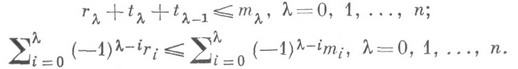
 последнее М. н. всегда является равенством, так что
последнее М. н. всегда является равенством, так что
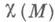 - эйлерова характеристика многообразия М.
- эйлерова характеристика многообразия М.
 достаточно заменить группы
достаточно заменить группы 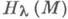 группами относительных гомологии
группами относительных гомологии  .
. существует функция Морса, для к-рой М. н. являются равенствами (Смейла теорема, см. [2]). В частности, на любом замкнутом многообразии, гомотопически эквивалентном сфере
существует функция Морса, для к-рой М. н. являются равенствами (Смейла теорема, см. [2]). В частности, на любом замкнутом многообразии, гомотопически эквивалентном сфере  , существует функция Морса с двумя критич. точками, откуда непосредственно следует (см. Морса теория), что многообразие Мгомеоморфно сфере
, существует функция Морса с двумя критич. точками, откуда непосредственно следует (см. Морса теория), что многообразие Мгомеоморфно сфере  (см. Пуанкаре гипотеза). Аналогичное применение теоремы Смейла позволяет доказать и теоремы об h- и s-кобордизмах.
(см. Пуанкаре гипотеза). Аналогичное применение теоремы Смейла позволяет доказать и теоремы об h- и s-кобордизмах.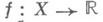 на бесконечномерных гильбертовых многообразиях и связывают (для любых регулярных значений
на бесконечномерных гильбертовых многообразиях и связывают (для любых регулярных значений 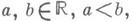 функции f) числа
функции f) числа  лежащих в
лежащих в  критич. точек конечного индекса
критич. точек конечного индекса  с рангом
с рангом  и периодич. рангом
и периодич. рангом  группы
группы  где
где  . Именно,
. Именно,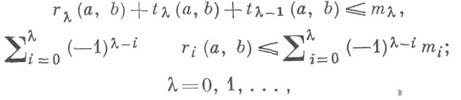
 последнее неравенство становится равенством.
последнее неравенство становится равенством.