"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МОРСА ЛЕММАЗначение МОРСА ЛЕММА в математической энциклопедии:
- утверждение, описывающее строение ростка дважды непрерывно дифференцируемой функции. Пусть  - функция класса - функция класса  , имеющая точку , имеющая точку  своей невырожденной критиче ской точкой. Тогда в нек-рой окрестности Uточки Осуществует такая система локальных координат (карта) своей невырожденной критиче ской точкой. Тогда в нек-рой окрестности Uточки Осуществует такая система локальных координат (карта) с центром в О, что для всех с центром в О, что для всех  имеет место равенство имеет место равенство 
При этом число  является Морса индексом критич. точки Офункции f. Справедлив также аналог М. л. для функций является Морса индексом критич. точки Офункции f. Справедлив также аналог М. л. для функций  именно: если f голоморфна в нек-рой окрестности своей невырожденной критич. точки (в другой терминологии - точки перевала, см. Перевала метод) именно: если f голоморфна в нек-рой окрестности своей невырожденной критич. точки (в другой терминологии - точки перевала, см. Перевала метод) , то в нек-рой окрестности Uточки Осуществует такая система локальных координат , то в нек-рой окрестности Uточки Осуществует такая система локальных координат  что что 
М. л. справедлива и для функций  на сепарабельном (бесконечномерном) гильбертовом пространстве Е. Пусть f дважды дифференцируема (по Фреше) в нек-рой окрестности своей невырожденной критич. точки на сепарабельном (бесконечномерном) гильбертовом пространстве Е. Пусть f дважды дифференцируема (по Фреше) в нек-рой окрестности своей невырожденной критич. точки  . Тогда существуют такая выпуклая окрестность нуля . Тогда существуют такая выпуклая окрестность нуля  , такая окрестность нуля , такая окрестность нуля  и такой диффеоморфизм (карта) и такой диффеоморфизм (карта) что для всех что для всех  имеет место равенство имеет место равенство 
где  - непрерывный ортогональный проектор, а I - тождественный оператор. При этом размерность - непрерывный ортогональный проектор, а I - тождественный оператор. При этом размерность  совпадает с индексом Морса критич. точки совпадает с индексом Морса критич. точки  функции функции  , а размерность , а размерность 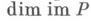 - с ее коиндексом. - с ее коиндексом. Лит.:[1] Моrse M., The calculus of variations in the large, N. Y., 1934. M. M. Постников, Ю. Б. Рудяк.
|

 - функция класса
- функция класса  , имеющая точку
, имеющая точку  своей невырожденной критиче ской точкой. Тогда в нек-рой окрестности Uточки Осуществует такая система локальных координат (карта)
своей невырожденной критиче ской точкой. Тогда в нек-рой окрестности Uточки Осуществует такая система локальных координат (карта) с центром в О, что для всех
с центром в О, что для всех  имеет место равенство
имеет место равенство
 является Морса индексом критич. точки Офункции f. Справедлив также аналог М. л. для функций
является Морса индексом критич. точки Офункции f. Справедлив также аналог М. л. для функций  именно: если f голоморфна в нек-рой окрестности своей невырожденной критич. точки (в другой терминологии - точки перевала, см. Перевала метод)
именно: если f голоморфна в нек-рой окрестности своей невырожденной критич. точки (в другой терминологии - точки перевала, см. Перевала метод) , то в нек-рой окрестности Uточки Осуществует такая система локальных координат
, то в нек-рой окрестности Uточки Осуществует такая система локальных координат  что
что
 на сепарабельном (бесконечномерном) гильбертовом пространстве Е. Пусть f дважды дифференцируема (по Фреше) в нек-рой окрестности своей невырожденной критич. точки
на сепарабельном (бесконечномерном) гильбертовом пространстве Е. Пусть f дважды дифференцируема (по Фреше) в нек-рой окрестности своей невырожденной критич. точки  . Тогда существуют такая выпуклая окрестность нуля
. Тогда существуют такая выпуклая окрестность нуля  , такая окрестность нуля
, такая окрестность нуля  и такой диффеоморфизм (карта)
и такой диффеоморфизм (карта) что для всех
что для всех  имеет место равенство
имеет место равенство
 - непрерывный ортогональный проектор, а I - тождественный оператор. При этом размерность
- непрерывный ортогональный проектор, а I - тождественный оператор. При этом размерность  совпадает с индексом Морса критич. точки
совпадает с индексом Морса критич. точки  функции
функции  , а размерность
, а размерность 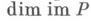 - с ее коиндексом.
- с ее коиндексом.