|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МОРЕРЫ ТЕОРЕМАЗначение МОРЕРЫ ТЕОРЕМА в математической энциклопедии: если (однозначная) функция
то f(z) - аналитич. ция в D. Эта теорема была получена Дж. Морерой [1]. Условие сформулированной М. т. можно ослабить, ограничившись требованием, чтобы обращались в нуль интегралы (*), взятые по границе М. т. обобщается на случай функций многих комплексных переменных. Пусть функция
где Лит.:[1] Morera G., "Rend. Ist. Lomb.", 1886, t. 19, p. 304-308; [2] Mapкушевич А. И., Теория аналитических функций, 2 изд., т. 1, М., 1967; [3] Шабат Б .В., Введение в комплексный анализ, 2 изд., ч. 1-2, М., 1976; [4] Владимиров В. С, Методы теории функций многих комплексных переменных, М., 1964. Е. Д. Соломенцев. |
|
|
|

 комплексного переменного z в области Dнепрерывна и интеграл от нее по любому замкнутому спрямляемому контуру
комплексного переменного z в области Dнепрерывна и интеграл от нее по любому замкнутому спрямляемому контуру  равен нулю, т. е.
равен нулю, т. е.
 любого треугольника
любого треугольника  , компактно принадлежащего области D, т. е. такого, что
, компактно принадлежащего области D, т. е. такого, что  . М. т. представляет собой (неполное) обращение Коши интегральной теоремы и является одной из основных теорем, теории аналитич. ций.
. М. т. представляет собой (неполное) обращение Коши интегральной теоремы и является одной из основных теорем, теории аналитич. ций.  комплексных переменных
комплексных переменных  непрерывна в области Dкомплексного пространства
непрерывна в области Dкомплексного пространства  и такова, что обращается в нуль интеграл от нее, взятый по границе
и такова, что обращается в нуль интеграл от нее, взятый по границе  любой компактно принадлежащей Dпризма-тич, области вида
любой компактно принадлежащей Dпризма-тич, области вида
 - прямолинейные отрезки в плоскостях
- прямолинейные отрезки в плоскостях  с концами
с концами  - треугольник в плоскости
- треугольник в плоскости 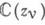 . Тогда
. Тогда  - голоморфная функция в D.
- голоморфная функция в D.