"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МОРДЕЛЛА ГИПОТЕЗА
Значение МОРДЕЛЛА ГИПОТЕЗА в математической энциклопедии:
- гипотеза о конечности множества рациональных точек на алгебраич. кривой рода  . Выдвинута Л. Морделлом [1] для случая, когда основное поле К- поле рациональных чисел. В настоящее время под М. г. понимается утверждение о конечности множества рациональных точек
. Выдвинута Л. Морделлом [1] для случая, когда основное поле К- поле рациональных чисел. В настоящее время под М. г. понимается утверждение о конечности множества рациональных точек  неприводимой алгебраич. кривой Xрода
неприводимой алгебраич. кривой Xрода  , определенной над полем Кконечного тина над полем рациональных чисел
, определенной над полем Кконечного тина над полем рациональных чисел 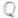 , в любом конечном расширении L/К. В такой форме М. г. не доказана (1982) ни для одной кривой. Получена редукция М. г. к наиболее трудному случаю, когда К- поле алгебраич. чисел (см. [3]). Известен ряд частных результатов, относящихся к М. г. Так, доказано [2], что множество
, в любом конечном расширении L/К. В такой форме М. г. не доказана (1982) ни для одной кривой. Получена редукция М. г. к наиболее трудному случаю, когда К- поле алгебраич. чисел (см. [3]). Известен ряд частных результатов, относящихся к М. г. Так, доказано [2], что множество 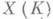 конечно, если ранг группы K-изоморфизмов из Xв эллиптич. кривую Yбольше ранга группы Y(К). Установлена [7] конечность X(К)для широкого класса модулярных кривых и их поля определения К. Найдена [8] оценка роста высот
конечно, если ранг группы K-изоморфизмов из Xв эллиптич. кривую Yбольше ранга группы Y(К). Установлена [7] конечность X(К)для широкого класса модулярных кривых и их поля определения К. Найдена [8] оценка роста высот
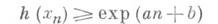
рациональных точек  , показывающая, что они расположены гораздо "реже", чем на кривых рода
, показывающая, что они расположены гораздо "реже", чем на кривых рода 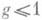 Доказано также, что М. г. является следствием гипотезы Шафаревича о конечности числа алгебраич. кривых, имеющих заданный род
Доказано также, что М. г. является следствием гипотезы Шафаревича о конечности числа алгебраич. кривых, имеющих заданный род  , поле определения (конечное расширение
, поле определения (конечное расширение  ) и множество точек плохой редукции (см. [4], а также Зигеля теорема о целых точках). Геометрич. аналогом М. г. является утверждение о конечности числа сечений у расслоения
) и множество точек плохой редукции (см. [4], а также Зигеля теорема о целых точках). Геометрич. аналогом М. г. является утверждение о конечности числа сечений у расслоения
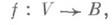
где 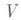 - неособая проективная поверхность, В- кривая, а общий слой отображения f - неприводимая кривая рода
- неособая проективная поверхность, В- кривая, а общий слой отображения f - неприводимая кривая рода  . Это утверждение верно, если расслоение непостоянно, т. е. не является прямым произведением после нек-рого накрытия базы В, и характеристика основного поля кравна 0 (см. [3], [6]). Для постоянных расслоений можно утверждать лишь конечность числа классов, состоящих из сечений, алгебраически эквивалентных как кривые на V. Если же характеристика поля кположительна, то геометрич. аналог М. г. для постоянных расслоений неверен [4].
. Это утверждение верно, если расслоение непостоянно, т. е. не является прямым произведением после нек-рого накрытия базы В, и характеристика основного поля кравна 0 (см. [3], [6]). Для постоянных расслоений можно утверждать лишь конечность числа классов, состоящих из сечений, алгебраически эквивалентных как кривые на V. Если же характеристика поля кположительна, то геометрич. аналог М. г. для постоянных расслоений неверен [4].
Лит.:[1] Моrdеll L. J., "Proc. Camb. Phil. Soc", 1922, v. 21, p. 179-92; [2] Демьяненко В. А., "Изв. АН СССР. Сер. матем.", 1966, т. 30, № 6, с. 1373-96; [3] Манин Ю. И., там же, 1963, т. 27, № 6, с. 1395-1440; [4] Раrsin А. N.. в кн.: Actes du Congres International des mathematiciens. 1970, t. 1, P., 1971, p. 467-71; [5] Grauert H., "Publ. Math. IHES", 1965, № 25, p. 131 - 50; [6] Lang S., Diophantine geometry, N. Y.- L., 1962; [7] Mаzur В., в кн.: Modular functions of one variable, [v. 5], В.- Hdlb.- N. Y., 1977, p. 107-48; [8] Mumfоrd D., "Amer. J. Math.", 1965, v. 87, № 4, p. 1007- 16.
A. H. Паршин.

 . Выдвинута Л. Морделлом [1] для случая, когда основное поле К- поле рациональных чисел. В настоящее время под М. г. понимается утверждение о конечности множества рациональных точек
. Выдвинута Л. Морделлом [1] для случая, когда основное поле К- поле рациональных чисел. В настоящее время под М. г. понимается утверждение о конечности множества рациональных точек  неприводимой алгебраич. кривой Xрода
неприводимой алгебраич. кривой Xрода  , определенной над полем Кконечного тина над полем рациональных чисел
, определенной над полем Кконечного тина над полем рациональных чисел 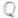 , в любом конечном расширении L/К. В такой форме М. г. не доказана (1982) ни для одной кривой. Получена редукция М. г. к наиболее трудному случаю, когда К- поле алгебраич. чисел (см. [3]). Известен ряд частных результатов, относящихся к М. г. Так, доказано [2], что множество
, в любом конечном расширении L/К. В такой форме М. г. не доказана (1982) ни для одной кривой. Получена редукция М. г. к наиболее трудному случаю, когда К- поле алгебраич. чисел (см. [3]). Известен ряд частных результатов, относящихся к М. г. Так, доказано [2], что множество 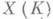 конечно, если ранг группы K-изоморфизмов из Xв эллиптич. кривую Yбольше ранга группы Y(К). Установлена [7] конечность X(К)для широкого класса модулярных кривых и их поля определения К. Найдена [8] оценка роста высот
конечно, если ранг группы K-изоморфизмов из Xв эллиптич. кривую Yбольше ранга группы Y(К). Установлена [7] конечность X(К)для широкого класса модулярных кривых и их поля определения К. Найдена [8] оценка роста высот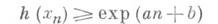
 , показывающая, что они расположены гораздо "реже", чем на кривых рода
, показывающая, что они расположены гораздо "реже", чем на кривых рода 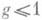 Доказано также, что М. г. является следствием гипотезы Шафаревича о конечности числа алгебраич. кривых, имеющих заданный род
Доказано также, что М. г. является следствием гипотезы Шафаревича о конечности числа алгебраич. кривых, имеющих заданный род  , поле определения (конечное расширение
, поле определения (конечное расширение  ) и множество точек плохой редукции (см. [4], а также Зигеля теорема о целых точках). Геометрич. аналогом М. г. является утверждение о конечности числа сечений у расслоения
) и множество точек плохой редукции (см. [4], а также Зигеля теорема о целых точках). Геометрич. аналогом М. г. является утверждение о конечности числа сечений у расслоения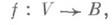
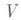 - неособая проективная поверхность, В- кривая, а общий слой отображения f - неприводимая кривая рода
- неособая проективная поверхность, В- кривая, а общий слой отображения f - неприводимая кривая рода  . Это утверждение верно, если расслоение непостоянно, т. е. не является прямым произведением после нек-рого накрытия базы В, и характеристика основного поля кравна 0 (см. [3], [6]). Для постоянных расслоений можно утверждать лишь конечность числа классов, состоящих из сечений, алгебраически эквивалентных как кривые на V. Если же характеристика поля кположительна, то геометрич. аналог М. г. для постоянных расслоений неверен [4].
. Это утверждение верно, если расслоение непостоянно, т. е. не является прямым произведением после нек-рого накрытия базы В, и характеристика основного поля кравна 0 (см. [3], [6]). Для постоянных расслоений можно утверждать лишь конечность числа классов, состоящих из сечений, алгебраически эквивалентных как кривые на V. Если же характеристика поля кположительна, то геометрич. аналог М. г. для постоянных расслоений неверен [4].