|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МОНОДРОМИИ ГРУППАЗначение МОНОДРОМИИ ГРУППА в математической энциклопедии: обыкновенного линейного дифференциального уравнения или линейной системы уравнений - группа (nХ n)-матриц, к-рая отвечает системе п- гопорядка
и определяется следующим образом. Пусть матрица
где При этом
где Т - постоянная матрица. М. г. вычислена для уравнений Эйлера, Папперитца (см. [1], [2]), Лит.:[1] Голубев В. В., Лекции по аналитической теории дифференциальных уравнений, 2 изд., М.- Л., 1950; [2] Айне Э. Л., Обыкновенные дифференциальные уравнения, пер. с англ., Хар., 1939. М. В. Федорюк. |
|
|
|


 голоморфна в области
голоморфна в области  , точка
, точка  - фундаментальная матрица системы (*), заданная в малой окрестности
- фундаментальная матрица системы (*), заданная в малой окрестности  Если
Если  - замкнутая кривая с началом в точке t0, то при аналитич. родолжении вдоль
- замкнутая кривая с началом в точке t0, то при аналитич. родолжении вдоль 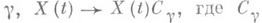 - постоянная
- постоянная  матрица. Если кривые
матрица. Если кривые  гомотопны в G, то
гомотопны в G, то 
 ; если
; если  Отображение
Отображение  есть гомоморфизм фундаментальной группы области G:
есть гомоморфизм фундаментальной группы области G:
 - группа
- группа  -матриц с комплексными элементами; образ этого гомоморфизма наз. группой монодромии
-матриц с комплексными элементами; образ этого гомоморфизма наз. группой монодромии  системы (*).
системы (*).