"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МОНОГЕННАЯ ФУНКЦИЯ
Значение МОНОГЕННАЯ ФУНКЦИЯ в математической энциклопедии:
- функция комплексного переменного, имеющая конечную производную.
Точнее, функция 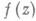 , определенная на множестве Екомплексной плоскости
, определенная на множестве Екомплексной плоскости  , наз. моногенной (относительно множества Е)в конечной неизолированной точке
, наз. моногенной (относительно множества Е)в конечной неизолированной точке  , если она имеет в этой точке конечную производную
, если она имеет в этой точке конечную производную  по переменному
по переменному  :
:

Функция, моногенная в каждой неизолированной точке множества Е, наз. моногенной на Е.
Если E=G- область плоскости  , то функция, моногенная на G, наз. аналитической функцией в области G.
, то функция, моногенная на G, наз. аналитической функцией в области G.
Если Ене является областью, то моногенные на Ефункции, вообще говоря, уже не обладают характерными свойствами аналитич. ций. Однако если множество Е, не содержащее в своем составе областей, является достаточно "массивным" вблизи большинства своих точек (точнее, если дополнение к Ев плоскости  является достаточно разреженным вблизи большинства точек
является достаточно разреженным вблизи большинства точек  ), то функции, моногенные на Е, обладают в ослабленном виде многими свойствами аналитич. ций. В попытках разобраться в глубинных связях между основными свойствами аналитич. ций понятие аналитич. ции обобщалось различными путями: посредством обобщения ее области определения, обобщения самого понятия производной, ослабления условий Кошп - Римана, ослабления условий теоремы Мореры и т. п. (см. [13] § 6). С этой же целью для "тощих" множеств Е, напр, для отрезка
), то функции, моногенные на Е, обладают в ослабленном виде многими свойствами аналитич. ций. В попытках разобраться в глубинных связях между основными свойствами аналитич. ций понятие аналитич. ции обобщалось различными путями: посредством обобщения ее области определения, обобщения самого понятия производной, ослабления условий Кошп - Римана, ослабления условий теоремы Мореры и т. п. (см. [13] § 6). С этой же целью для "тощих" множеств Е, напр, для отрезка 
 выделялись т. н. квазианалитические классы функций. Изучались также функции, определенные на нигде не плотных достаточно массивных компактах Е, близкие аналитич. циям в том смысле, что они могут быть с любой точностью равномерно на Еприближены аналитич. циями или, что то же самое, рациональными функциями переменной z.
выделялись т. н. квазианалитические классы функций. Изучались также функции, определенные на нигде не плотных достаточно массивных компактах Е, близкие аналитич. циям в том смысле, что они могут быть с любой точностью равномерно на Еприближены аналитич. циями или, что то же самое, рациональными функциями переменной z.
Ниже приведены нек-рые результаты из перечисленных направлений.
1. Функции, моногенные в области. Если 
 (при этом
(при этом  и
и  - действительнозначные функции), то для аналитичности
- действительнозначные функции), то для аналитичности  в области Gдостаточно (и необходимо) выполнения в каждой точке
в области Gдостаточно (и необходимо) выполнения в каждой точке  одновременно двух условий:
одновременно двух условий:
1) имеют полные дифференциалы
имеют полные дифференциалы  и
и  по совокупности действительных переменных (x, y); 2) выполнены условия Коши - Римана:
по совокупности действительных переменных (x, y); 2) выполнены условия Коши - Римана:

Условия этой теоремы ослаблялись и обобщались. Напр., показано, что требование существования полных дифференциалов у  и
и  можно заменить существенно более слабым условием ограниченности
можно заменить существенно более слабым условием ограниченности  и
и  в
в  и, сохранив требование существования первых частных производных функций
и, сохранив требование существования первых частных производных функций  и
и  всюду в G, потребовать выполнение условий Коши - Римана лишь почти всюду в G(в смысле плоской меры, Лебега) (см. [6]).
всюду в G, потребовать выполнение условий Коши - Римана лишь почти всюду в G(в смысле плоской меры, Лебега) (см. [6]).
Пусть  - какая-либо пара различных прямых, пересекающихся в точке z, R(z) - какая-либо тройка выходящих из z попарно неколлинеарных лучей и Е(z) - какое-либо измеримое множество, имеющее z своей точкой плотности в смысле Лебега. Аналитичность непрерывной в Gфункции f(z) обеспечивается каждым из следующих условий в отдельности (см. [3] - [5]): а) всюду в Gсуществует
- какая-либо пара различных прямых, пересекающихся в точке z, R(z) - какая-либо тройка выходящих из z попарно неколлинеарных лучей и Е(z) - какое-либо измеримое множество, имеющее z своей точкой плотности в смысле Лебега. Аналитичность непрерывной в Gфункции f(z) обеспечивается каждым из следующих условий в отдельности (см. [3] - [5]): а) всюду в Gсуществует  б) всюду в Gсуществует
б) всюду в Gсуществует  в) всюду в Gсуществует
в) всюду в Gсуществует  . Здесь каждое из множеств L(z), R(z), Е(z) - свое для каждой точки. Следует заметить, что
. Здесь каждое из множеств L(z), R(z), Е(z) - свое для каждой точки. Следует заметить, что  зависит от f и z, но не зависит от Е(z); производная
зависит от f и z, но не зависит от Е(z); производная  наз. асимптотической (аппроксимативной) производной, а функция, имеющая аеймптотич. производную в точке z(соответственно в области G), наз. асимптотически моногенной в точке z (соответственно в G). Вместо условия б) достаточно потребовать существования предела для
наз. асимптотической (аппроксимативной) производной, а функция, имеющая аеймптотич. производную в точке z(соответственно в области G), наз. асимптотически моногенной в точке z (соответственно в G). Вместо условия б) достаточно потребовать существования предела для

2. Функции, моногенные на нигде не плотных множествах. Э. Борель [8] построил такое совершенное связное множество (континуум) Ебез внутренних точек и такую расширяющуюся последовательность  совершенных множеств, что площадь
совершенных множеств, что площадь  множества Еположительна,
множества Еположительна,  и из моногенности f(z) на Е(или хотя бы на каждом множестве
и из моногенности f(z) на Е(или хотя бы на каждом множестве  ) следует бесконечная дифференцируемость
) следует бесконечная дифференцируемость  по
по  при каждом фиксированном
при каждом фиксированном  . Можно указать нек-рые сравнительно общие достаточные условия на Е, чтобы Еобладало этим свойством или более слабым свойством k-кратной дифференцируемости по
. Можно указать нек-рые сравнительно общие достаточные условия на Е, чтобы Еобладало этим свойством или более слабым свойством k-кратной дифференцируемости по  , где k- наперед заданное натуральное число. Найдены также достаточные условия на нигде не плотный континуум Едля того, чтобы для функций, моногенных на нем, были справедливы аналоги интегральной теоремы Коши, разложения в ряд Тейлора и различные формы теоремы единственности, напр, такая: если моногенные на Ефункции f1 (z) и f2 (z) совпадают на нек-рой порции множества Е(т. е. на непустом пересечении Ес нек-рым открытым кругом), то
, где k- наперед заданное натуральное число. Найдены также достаточные условия на нигде не плотный континуум Едля того, чтобы для функций, моногенных на нем, были справедливы аналоги интегральной теоремы Коши, разложения в ряд Тейлора и различные формы теоремы единственности, напр, такая: если моногенные на Ефункции f1 (z) и f2 (z) совпадают на нек-рой порции множества Е(т. е. на непустом пересечении Ес нек-рым открытым кругом), то  на Е(см. [9]).
на Е(см. [9]).
3. Функции, близкие к аналитическим. Как известно, любая аналитическая в области Gфункция f(z)является пределом нек-рой последовательности рациональных функций  , к-рая сходится к f(z) равномерно на каждом компакте
, к-рая сходится к f(z) равномерно на каждом компакте  . Рассматривая достаточно массивный нигде не плотный континуум Еи класс
. Рассматривая достаточно массивный нигде не плотный континуум Еи класс  функций
функций  для каждой из к-рых существует последовательность рациональных функций
для каждой из к-рых существует последовательность рациональных функций  равномерно сходящаяся к
равномерно сходящаяся к  получают еще одно обобщение понятия области и понятия функции f(z), аналитической на Е. Если Е - нигде не плотное множество на
получают еще одно обобщение понятия области и понятия функции f(z), аналитической на Е. Если Е - нигде не плотное множество на  , то всегда найдется функция
, то всегда найдется функция  не имеющая производной
не имеющая производной  ни в одной точке
ни в одной точке  (см. [10]). Однако для каждого
(см. [10]). Однако для каждого  можно указать условие на Е, при выполнении к-рого каждая функция
можно указать условие на Е, при выполнении к-рого каждая функция  будет иметь производные
будет иметь производные  , где
, где  замкнуто,
замкнуто, (см. [11]). М. В. Келдыш построил пример нигде не плотного континуума Е, на к-ром для функций
(см. [11]). М. В. Келдыш построил пример нигде не плотного континуума Е, на к-ром для функций  ,
,  справедлива теорема единственности в форме, приведенной в конце п. 2 (см. также [12]). (По поводу моногенных свойств функций из R(Е)в терминах функционального анализа см. [12] ч. I, § 17.) Исследовалась также зависимость моногенных свойств функций
справедлива теорема единственности в форме, приведенной в конце п. 2 (см. также [12]). (По поводу моногенных свойств функций из R(Е)в терминах функционального анализа см. [12] ч. I, § 17.) Исследовалась также зависимость моногенных свойств функций  от скорости приближения ее посредством рациональных функций.
от скорости приближения ее посредством рациональных функций.
Лит.:[1] Федоров В. С, "Успехи матем. наук", 1952, т. 7, в. 2, с. 7 - 16; [2] Воhr H.. "Math. Z.", 1918, Bd I, S. 403-20; [3] Меньшов Д. Е., "Fundam. math.", 1935, v. 25 p. 59-97; [4] его же, Les conditions de monogeneite, P., 1936; [5] его же, "Матем. сб.", 1936, т. .1, с. 189-210; [6] Толстов Г. П., О криволинейном и повторном интеграле, М.-Л.. 1950 (Тр. Матем. ин-та АН СССР, т. 35); [7] Трохимчук Ю. Ю., Непрерывные отображения и условия моногенности, М., 1963; [8] Borel E., Lecons sur les fonctions monogenes uniformes d'une variable complexe, P., 1917; [9] Селезнев A. И., "Докл. АН СССР", 1956, т. 108, № 4, с. 591-94; 110] Долженко Е. П., там же, 1959, т. 125, № 5, с. 970- 973; [11] его ж е, там же, 1962, т. 143, №4, с. 771-74; [12] Итоги науки и техники. Современные проблемы математики, т. 4, М., 1975, с. 143-250: [13] Бермант А. Ф., Маркушевич А. И., в кн.: Математика в СССР за тридцать лет. 1917 - 1947 М.- Л., 1948, с. 401-406.
Е. П. Долженко.

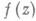 , определенная на множестве Екомплексной плоскости
, определенная на множестве Екомплексной плоскости  , наз. моногенной (относительно множества Е)в конечной неизолированной точке
, наз. моногенной (относительно множества Е)в конечной неизолированной точке  , если она имеет в этой точке конечную производную
, если она имеет в этой точке конечную производную  по переменному
по переменному  :
:
 , то функция, моногенная на G, наз. аналитической функцией в области G.
, то функция, моногенная на G, наз. аналитической функцией в области G. является достаточно разреженным вблизи большинства точек
является достаточно разреженным вблизи большинства точек  ), то функции, моногенные на Е, обладают в ослабленном виде многими свойствами аналитич. ций. В попытках разобраться в глубинных связях между основными свойствами аналитич. ций понятие аналитич. ции обобщалось различными путями: посредством обобщения ее области определения, обобщения самого понятия производной, ослабления условий Кошп - Римана, ослабления условий теоремы Мореры и т. п. (см. [13] § 6). С этой же целью для "тощих" множеств Е, напр, для отрезка
), то функции, моногенные на Е, обладают в ослабленном виде многими свойствами аналитич. ций. В попытках разобраться в глубинных связях между основными свойствами аналитич. ций понятие аналитич. ции обобщалось различными путями: посредством обобщения ее области определения, обобщения самого понятия производной, ослабления условий Кошп - Римана, ослабления условий теоремы Мореры и т. п. (см. [13] § 6). С этой же целью для "тощих" множеств Е, напр, для отрезка 
 выделялись т. н. квазианалитические классы функций. Изучались также функции, определенные на нигде не плотных достаточно массивных компактах Е, близкие аналитич. циям в том смысле, что они могут быть с любой точностью равномерно на Еприближены аналитич. циями или, что то же самое, рациональными функциями переменной z.
выделялись т. н. квазианалитические классы функций. Изучались также функции, определенные на нигде не плотных достаточно массивных компактах Е, близкие аналитич. циям в том смысле, что они могут быть с любой точностью равномерно на Еприближены аналитич. циями или, что то же самое, рациональными функциями переменной z.
 (при этом
(при этом  и
и  - действительнозначные функции), то для аналитичности
- действительнозначные функции), то для аналитичности  в области Gдостаточно (и необходимо) выполнения в каждой точке
в области Gдостаточно (и необходимо) выполнения в каждой точке  одновременно двух условий:
одновременно двух условий: имеют полные дифференциалы
имеют полные дифференциалы  и
и  по совокупности действительных переменных (x, y); 2) выполнены условия Коши - Римана:
по совокупности действительных переменных (x, y); 2) выполнены условия Коши - Римана:
 и
и  можно заменить существенно более слабым условием ограниченности
можно заменить существенно более слабым условием ограниченности  и
и  в
в  и, сохранив требование существования первых частных производных функций
и, сохранив требование существования первых частных производных функций  и
и  всюду в G, потребовать выполнение условий Коши - Римана лишь почти всюду в G(в смысле плоской меры, Лебега) (см. [6]).
всюду в G, потребовать выполнение условий Коши - Римана лишь почти всюду в G(в смысле плоской меры, Лебега) (см. [6]). - какая-либо пара различных прямых, пересекающихся в точке z, R(z) - какая-либо тройка выходящих из z попарно неколлинеарных лучей и Е(z) - какое-либо измеримое множество, имеющее z своей точкой плотности в смысле Лебега. Аналитичность непрерывной в Gфункции f(z) обеспечивается каждым из следующих условий в отдельности (см. [3] - [5]): а) всюду в Gсуществует
- какая-либо пара различных прямых, пересекающихся в точке z, R(z) - какая-либо тройка выходящих из z попарно неколлинеарных лучей и Е(z) - какое-либо измеримое множество, имеющее z своей точкой плотности в смысле Лебега. Аналитичность непрерывной в Gфункции f(z) обеспечивается каждым из следующих условий в отдельности (см. [3] - [5]): а) всюду в Gсуществует  б) всюду в Gсуществует
б) всюду в Gсуществует  в) всюду в Gсуществует
в) всюду в Gсуществует  . Здесь каждое из множеств L(z), R(z), Е(z) - свое для каждой точки. Следует заметить, что
. Здесь каждое из множеств L(z), R(z), Е(z) - свое для каждой точки. Следует заметить, что  зависит от f и z, но не зависит от Е(z); производная
зависит от f и z, но не зависит от Е(z); производная  наз. асимптотической (аппроксимативной) производной, а функция, имеющая аеймптотич. производную в точке z(соответственно в области G), наз. асимптотически моногенной в точке z (соответственно в G). Вместо условия б) достаточно потребовать существования предела для
наз. асимптотической (аппроксимативной) производной, а функция, имеющая аеймптотич. производную в точке z(соответственно в области G), наз. асимптотически моногенной в точке z (соответственно в G). Вместо условия б) достаточно потребовать существования предела для
 совершенных множеств, что площадь
совершенных множеств, что площадь  множества Еположительна,
множества Еположительна,  и из моногенности f(z) на Е(или хотя бы на каждом множестве
и из моногенности f(z) на Е(или хотя бы на каждом множестве  ) следует бесконечная дифференцируемость
) следует бесконечная дифференцируемость  по
по  при каждом фиксированном
при каждом фиксированном  . Можно указать нек-рые сравнительно общие достаточные условия на Е, чтобы Еобладало этим свойством или более слабым свойством k-кратной дифференцируемости по
. Можно указать нек-рые сравнительно общие достаточные условия на Е, чтобы Еобладало этим свойством или более слабым свойством k-кратной дифференцируемости по  , где k- наперед заданное натуральное число. Найдены также достаточные условия на нигде не плотный континуум Едля того, чтобы для функций, моногенных на нем, были справедливы аналоги интегральной теоремы Коши, разложения в ряд Тейлора и различные формы теоремы единственности, напр, такая: если моногенные на Ефункции f1 (z) и f2 (z) совпадают на нек-рой порции множества Е(т. е. на непустом пересечении Ес нек-рым открытым кругом), то
, где k- наперед заданное натуральное число. Найдены также достаточные условия на нигде не плотный континуум Едля того, чтобы для функций, моногенных на нем, были справедливы аналоги интегральной теоремы Коши, разложения в ряд Тейлора и различные формы теоремы единственности, напр, такая: если моногенные на Ефункции f1 (z) и f2 (z) совпадают на нек-рой порции множества Е(т. е. на непустом пересечении Ес нек-рым открытым кругом), то  на Е(см. [9]).
на Е(см. [9]). , к-рая сходится к f(z) равномерно на каждом компакте
, к-рая сходится к f(z) равномерно на каждом компакте  . Рассматривая достаточно массивный нигде не плотный континуум Еи класс
. Рассматривая достаточно массивный нигде не плотный континуум Еи класс  функций
функций  для каждой из к-рых существует последовательность рациональных функций
для каждой из к-рых существует последовательность рациональных функций  равномерно сходящаяся к
равномерно сходящаяся к  получают еще одно обобщение понятия области и понятия функции f(z), аналитической на Е. Если Е - нигде не плотное множество на
получают еще одно обобщение понятия области и понятия функции f(z), аналитической на Е. Если Е - нигде не плотное множество на  , то всегда найдется функция
, то всегда найдется функция  не имеющая производной
не имеющая производной  ни в одной точке
ни в одной точке  (см. [10]). Однако для каждого
(см. [10]). Однако для каждого  можно указать условие на Е, при выполнении к-рого каждая функция
можно указать условие на Е, при выполнении к-рого каждая функция  будет иметь производные
будет иметь производные  , где
, где  замкнуто,
замкнуто, (см. [11]). М. В. Келдыш построил пример нигде не плотного континуума Е, на к-ром для функций
(см. [11]). М. В. Келдыш построил пример нигде не плотного континуума Е, на к-ром для функций  ,
,  справедлива теорема единственности в форме, приведенной в конце п. 2 (см. также [12]). (По поводу моногенных свойств функций из R(Е)в терминах функционального анализа см. [12] ч. I, § 17.) Исследовалась также зависимость моногенных свойств функций
справедлива теорема единственности в форме, приведенной в конце п. 2 (см. также [12]). (По поводу моногенных свойств функций из R(Е)в терминах функционального анализа см. [12] ч. I, § 17.) Исследовалась также зависимость моногенных свойств функций  от скорости приближения ее посредством рациональных функций.
от скорости приближения ее посредством рациональных функций.