"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МОДУЛЯРНАЯ КРИВАЯ
Значение МОДУЛЯРНАЯ КРИВАЯ в математической энциклопедии:
- полная алгебраич. кривая  , униформизуемая подгруппой
, униформизуемая подгруппой  конечного индекса модулярной группы Г; точнее, М. к. есть полная алгебраич. кривая, получаемая из факторпро-странства
конечного индекса модулярной группы Г; точнее, М. к. есть полная алгебраич. кривая, получаемая из факторпро-странства  , где Н- верхняя полуплоскость, присоединением конечного числа параболич. точек (классов эквивалентности относительно
, где Н- верхняя полуплоскость, присоединением конечного числа параболич. точек (классов эквивалентности относительно  рациональных точек границы области Н). Наиболее известные примеры подгрупп
рациональных точек границы области Н). Наиболее известные примеры подгрупп  конечного индекса в Г - конгруэнц-подгруппы, содержащие для нек-рого целого
конечного индекса в Г - конгруэнц-подгруппы, содержащие для нек-рого целого  главную конгруэнц-подгруппу
главную конгруэнц-подгруппу  уровня N, представимую матрицами
уровня N, представимую матрицами

(см. Модулярная группа). Наименьшее такое Nназ. уровнем подгруппы  . В частности, подгруппа
. В частности, подгруппа  , представимая матрицами, к-рые сравнимы с верхними треугольными матрицами по mod N, имеет уровень N. Каждой подгруппе
, представимая матрицами, к-рые сравнимы с верхними треугольными матрицами по mod N, имеет уровень N. Каждой подгруппе 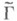 конечного индекса соответствует накрытие М. к.
конечного индекса соответствует накрытие М. к.  , к-рое разветвлено только над образами точек
, к-рое разветвлено только над образами точек 
 . Для конгруэнц-подгрупп
. Для конгруэнц-подгрупп  ветвление этого накрытия позволяет определить род М. к.
ветвление этого накрытия позволяет определить род М. к.  , доказать существование подгрупп Г конечного индекса в Г, не являющихся конгруэнц-подгруппами (см. [4] т. 2 и [2]). Род кривой
, доказать существование подгрупп Г конечного индекса в Г, не являющихся конгруэнц-подгруппами (см. [4] т. 2 и [2]). Род кривой  равен 0 для
равен 0 для  и равен
и равен

р - простые, при  . М. к. всегда определена над полем алгебраич. чисел (обычно над
. М. к. всегда определена над полем алгебраич. чисел (обычно над  или его круговым расширением). Рациональные функции на М. к. поднимаются до модулярных функций (высшего уровня) и образуют поле; автоморфизмы этого, поля изучены (см. [2]). Голоморфная дифференциальная форма на М. к.
или его круговым расширением). Рациональные функции на М. к. поднимаются до модулярных функций (высшего уровня) и образуют поле; автоморфизмы этого, поля изучены (см. [2]). Голоморфная дифференциальная форма на М. к. задается на Ндифференциалом
задается на Ндифференциалом  (где
(где  - голоморфная функция), инвариантным относительно преобразований
- голоморфная функция), инвариантным относительно преобразований  при этом
при этом  есть модулярная форма веса 2 относительно Г. Дзета-функция М. к. есть произведение Меллина преобразований модулярных форм и, следовательно, она имеет мероморфное продолжение и удовлетворяет функциональному уравнению. Этот факт послужил отправной точкой теории Ленглендса - Вейля о связи модулярных форм и рядов Дирихле (см. [7], [8]). В частности, есть предположение, что каждая зллиптич. кривая над полем
есть модулярная форма веса 2 относительно Г. Дзета-функция М. к. есть произведение Меллина преобразований модулярных форм и, следовательно, она имеет мероморфное продолжение и удовлетворяет функциональному уравнению. Этот факт послужил отправной точкой теории Ленглендса - Вейля о связи модулярных форм и рядов Дирихле (см. [7], [8]). В частности, есть предположение, что каждая зллиптич. кривая над полем  (кондуктора N)униформизуется модулярными функциями уровня N. Гомологии М. к. связаны с модулярными символами, что позволяет исследовать арифметику значений дзетафункции М. к. в центре критич. полосы и построить р-адическую дзета-функцию М. к. (см. [1]).
(кондуктора N)униформизуется модулярными функциями уровня N. Гомологии М. к. связаны с модулярными символами, что позволяет исследовать арифметику значений дзетафункции М. к. в центре критич. полосы и построить р-адическую дзета-функцию М. к. (см. [1]).
М. к. параметризует семейство эллиптич. кривых, являясь их многообразием модулей (см. [7] т. 2). В частности, для  точки
точки  факторпространства
факторпространства  взаимно однозначно соответствуют парам, состоящим из эллиптич. кривой
взаимно однозначно соответствуют парам, состоящим из эллиптич. кривой  (аналитически эквивалентной комплексному тору
(аналитически эквивалентной комплексному тору  ) и точки порядка Nна
) и точки порядка Nна  (образа точки z/N).
(образа точки z/N).
Над каждой М. к.  имеется естественное алгебраич. расслоение
имеется естественное алгебраич. расслоение  на эллиптич. кривые, компактифицированное вырожденными кривыми над параболич. точками М. к.
на эллиптич. кривые, компактифицированное вырожденными кривыми над параболич. точками М. к.  . Его расслоенные степени
. Его расслоенные степени  , где
, где  - целое
- целое  , наз. многообразиями Куги (см. [3], [5]). Дзета-функции многообразий
, наз. многообразиями Куги (см. [3], [5]). Дзета-функции многообразий  связаны с преобразованиями Меллина модулярных форм, а их гомологии - с периодами модулярных форм (см. [3], [7]).
связаны с преобразованиями Меллина модулярных форм, а их гомологии - с периодами модулярных форм (см. [3], [7]).
Рациональные точки на М. к. соответствуют эллиптич. кривым, имеющим рациональные точки конечного порядка (или рациональные подгруппы точек), их описание (см. [6]) позволило решить проблему кручения эллиптйч. кривых над 
Исследование геометрии и арифметики М. к. основано на использовании группы автоморфизмов проективного предела кривых  по убывающим
по убывающим  , края (по существу) совпадает с группой
, края (по существу) совпадает с группой  над кольцом Арациональных аделей. На каждой М. к.
над кольцом Арациональных аделей. На каждой М. к.  это дает нетривиальное кольцо соответствий
это дает нетривиальное кольцо соответствий  (кольцо Гекке), имеющее приложения в теории модулярных форм (см. [2]).
(кольцо Гекке), имеющее приложения в теории модулярных форм (см. [2]).
Лит.:[1] Манин Ю. И., "Изв. АН СССР. Сер. матем.", 1972, т. 36, №1, с. 19-66; [2] Шимура Г., Введение в арифметическую теорию автоморфныхфункций, пер. с англ., М., 1973; [3] Шокуро в В. В., "Матем. сб.", 1976, т. 101, № 1, с. 131 - 1 57; [4] Кlеin F., Pricke R., Vorlesungen uber die Theorie der elliptischen Modulfunktionen, Bd 1-2, Lpz., 1890-92; [5] Кuga M., ShimuraG., "Ann. Math.", 1965, v. 82, p. 478- 539; [6] Mazur В., Serre J.-P., в кн.: Seminaire Bourbaki, 1974/75, В.-[u. a.], 1976, p. 238-55; [7] Modular functions of one variable, [v.] 1-6, . В.- Hdlb.-N. Y., 1973-77;, [8] Weil A., "Math. Ann.", 1967, Bd 168, S. 149-56... ,.
А. А. Панчишкин, А. И. Паршин.

 , униформизуемая подгруппой
, униформизуемая подгруппой  конечного индекса модулярной группы Г; точнее, М. к. есть полная алгебраич. кривая, получаемая из факторпро-странства
конечного индекса модулярной группы Г; точнее, М. к. есть полная алгебраич. кривая, получаемая из факторпро-странства  , где Н- верхняя полуплоскость, присоединением конечного числа параболич. точек (классов эквивалентности относительно
, где Н- верхняя полуплоскость, присоединением конечного числа параболич. точек (классов эквивалентности относительно  рациональных точек границы области Н). Наиболее известные примеры подгрупп
рациональных точек границы области Н). Наиболее известные примеры подгрупп  конечного индекса в Г - конгруэнц-подгруппы, содержащие для нек-рого целого
конечного индекса в Г - конгруэнц-подгруппы, содержащие для нек-рого целого  главную конгруэнц-подгруппу
главную конгруэнц-подгруппу  уровня N, представимую матрицами
уровня N, представимую матрицами
 . В частности, подгруппа
. В частности, подгруппа  , представимая матрицами, к-рые сравнимы с верхними треугольными матрицами по mod N, имеет уровень N. Каждой подгруппе
, представимая матрицами, к-рые сравнимы с верхними треугольными матрицами по mod N, имеет уровень N. Каждой подгруппе 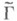 конечного индекса соответствует накрытие М. к.
конечного индекса соответствует накрытие М. к.  , к-рое разветвлено только над образами точек
, к-рое разветвлено только над образами точек 
 . Для конгруэнц-подгрупп
. Для конгруэнц-подгрупп  ветвление этого накрытия позволяет определить род М. к.
ветвление этого накрытия позволяет определить род М. к.  , доказать существование подгрупп Г конечного индекса в Г, не являющихся конгруэнц-подгруппами (см. [4] т. 2 и [2]). Род кривой
, доказать существование подгрупп Г конечного индекса в Г, не являющихся конгруэнц-подгруппами (см. [4] т. 2 и [2]). Род кривой  равен 0 для
равен 0 для  и равен
и равен 
 . М. к. всегда определена над полем алгебраич. чисел (обычно над
. М. к. всегда определена над полем алгебраич. чисел (обычно над  или его круговым расширением). Рациональные функции на М. к. поднимаются до модулярных функций (высшего уровня) и образуют поле; автоморфизмы этого, поля изучены (см. [2]). Голоморфная дифференциальная форма на М. к.
или его круговым расширением). Рациональные функции на М. к. поднимаются до модулярных функций (высшего уровня) и образуют поле; автоморфизмы этого, поля изучены (см. [2]). Голоморфная дифференциальная форма на М. к. задается на Ндифференциалом
задается на Ндифференциалом  (где
(где  - голоморфная функция), инвариантным относительно преобразований
- голоморфная функция), инвариантным относительно преобразований  при этом
при этом  есть модулярная форма веса 2 относительно Г. Дзета-функция М. к. есть произведение Меллина преобразований модулярных форм и, следовательно, она имеет мероморфное продолжение и удовлетворяет функциональному уравнению. Этот факт послужил отправной точкой теории Ленглендса - Вейля о связи модулярных форм и рядов Дирихле (см. [7], [8]). В частности, есть предположение, что каждая зллиптич. кривая над полем
есть модулярная форма веса 2 относительно Г. Дзета-функция М. к. есть произведение Меллина преобразований модулярных форм и, следовательно, она имеет мероморфное продолжение и удовлетворяет функциональному уравнению. Этот факт послужил отправной точкой теории Ленглендса - Вейля о связи модулярных форм и рядов Дирихле (см. [7], [8]). В частности, есть предположение, что каждая зллиптич. кривая над полем  (кондуктора N)униформизуется модулярными функциями уровня N. Гомологии М. к. связаны с модулярными символами, что позволяет исследовать арифметику значений дзетафункции М. к. в центре критич. полосы и построить р-адическую дзета-функцию М. к. (см. [1]).
(кондуктора N)униформизуется модулярными функциями уровня N. Гомологии М. к. связаны с модулярными символами, что позволяет исследовать арифметику значений дзетафункции М. к. в центре критич. полосы и построить р-адическую дзета-функцию М. к. (см. [1]).  точки
точки  факторпространства
факторпространства  взаимно однозначно соответствуют парам, состоящим из эллиптич. кривой
взаимно однозначно соответствуют парам, состоящим из эллиптич. кривой  (аналитически эквивалентной комплексному тору
(аналитически эквивалентной комплексному тору  ) и точки порядка Nна
) и точки порядка Nна  (образа точки z/N).
(образа точки z/N). имеется естественное алгебраич. расслоение
имеется естественное алгебраич. расслоение  на эллиптич. кривые, компактифицированное вырожденными кривыми над параболич. точками М. к.
на эллиптич. кривые, компактифицированное вырожденными кривыми над параболич. точками М. к.  . Его расслоенные степени
. Его расслоенные степени  , где
, где  - целое
- целое  , наз. многообразиями Куги (см. [3], [5]). Дзета-функции многообразий
, наз. многообразиями Куги (см. [3], [5]). Дзета-функции многообразий  связаны с преобразованиями Меллина модулярных форм, а их гомологии - с периодами модулярных форм (см. [3], [7]).
связаны с преобразованиями Меллина модулярных форм, а их гомологии - с периодами модулярных форм (см. [3], [7]).
 по убывающим
по убывающим  , края (по существу) совпадает с группой
, края (по существу) совпадает с группой  над кольцом Арациональных аделей. На каждой М. к.
над кольцом Арациональных аделей. На каждой М. к.  это дает нетривиальное кольцо соответствий
это дает нетривиальное кольцо соответствий  (кольцо Гекке), имеющее приложения в теории модулярных форм (см. [2]).
(кольцо Гекке), имеющее приложения в теории модулярных форм (см. [2]).