"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МОДУЛЬ АВТОМОРФИЗМА
Значение МОДУЛЬ АВТОМОРФИЗМА в математической энциклопедии:
- действительное положительное число, ставящееся в соответствие автоморфизму локально компактной группы. Если G- такая группа и  - нек-рый автоморфизм группы Gкак топологич. группы, то модуль автоморфизма
- нек-рый автоморфизм группы Gкак топологич. группы, то модуль автоморфизма  определяется формулой
определяется формулой

где 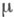 - левоинвариантная мера Хаара на группе Gи
- левоинвариантная мера Хаара на группе Gи  - любое компактное подмножество группы Gположительной меры (причем
- любое компактное подмножество группы Gположительной меры (причем  не зависит от S). Если G компактна или дискретна, то всегда
не зависит от S). Если G компактна или дискретна, то всегда  =
=  , т. к. для компактной группы можно положить
, т. к. для компактной группы можно положить  , а для дискретной
, а для дискретной  , где
, где  - любой элемент G.
- любой элемент G.
Если  и
и  - два автоморфизма группы G, то
- два автоморфизма группы G, то 
Если Г - нек-рая топологич. группа, к-рая непрерывно действует на группу Gавтоморфизмами, то  определяет непрерывный гомоморфизм
определяет непрерывный гомоморфизм  где
где  - мультипликативная группа действительных положительных чисел. В частности, сопоставляя каждому элементу
- мультипликативная группа действительных положительных чисел. В частности, сопоставляя каждому элементу  порождаемый им внутренний автоморфизм группы G и рассматривая модуль этого автоморфизма, получают непрерывный гомоморфизм Gв группу
порождаемый им внутренний автоморфизм группы G и рассматривая модуль этого автоморфизма, получают непрерывный гомоморфизм Gв группу  . Этот гомоморфизм тривиален тогда и только тогда, когда левоинвариантная мера Хаара на группе Gявляется одновременно и правоинвариантной. Группы, удовлетворяющие последнему условию, наз. унимодулярными.
. Этот гомоморфизм тривиален тогда и только тогда, когда левоинвариантная мера Хаара на группе Gявляется одновременно и правоинвариантной. Группы, удовлетворяющие последнему условию, наз. унимодулярными.
Другой пример - локально компактное тело К, каждый ненулевой элемент  к-рого определяет автоморфизм умножения на
к-рого определяет автоморфизм умножения на  аддитивной группы тела К. Функция
аддитивной группы тела К. Функция  используется при изучении структуры локально компактных тел.
используется при изучении структуры локально компактных тел.
Лит.:[1] Бурбаки Н., Интегрирование. Векторное интегрирование. Мера Хаара. Свертка и представления, пер. с франц., М., 1970; [2] Вейль А., Интегрирование в топологических группах и его применения, пер. с франц., М., 1950; [3] его же, Основы теории чисел, пер. с англ., М., 1972.
Л. В. Кузьмин.

 - нек-рый автоморфизм группы Gкак топологич. группы, то модуль автоморфизма
- нек-рый автоморфизм группы Gкак топологич. группы, то модуль автоморфизма  определяется формулой
определяется формулой
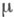 - левоинвариантная мера Хаара на группе Gи
- левоинвариантная мера Хаара на группе Gи  - любое компактное подмножество группы Gположительной меры (причем
- любое компактное подмножество группы Gположительной меры (причем  не зависит от S). Если G компактна или дискретна, то всегда
не зависит от S). Если G компактна или дискретна, то всегда  =
=  , т. к. для компактной группы можно положить
, т. к. для компактной группы можно положить  , а для дискретной
, а для дискретной  , где
, где  - любой элемент G.
- любой элемент G. и
и  - два автоморфизма группы G, то
- два автоморфизма группы G, то 
 определяет непрерывный гомоморфизм
определяет непрерывный гомоморфизм  где
где  - мультипликативная группа действительных положительных чисел. В частности, сопоставляя каждому элементу
- мультипликативная группа действительных положительных чисел. В частности, сопоставляя каждому элементу  порождаемый им внутренний автоморфизм группы G и рассматривая модуль этого автоморфизма, получают непрерывный гомоморфизм Gв группу
порождаемый им внутренний автоморфизм группы G и рассматривая модуль этого автоморфизма, получают непрерывный гомоморфизм Gв группу  . Этот гомоморфизм тривиален тогда и только тогда, когда левоинвариантная мера Хаара на группе Gявляется одновременно и правоинвариантной. Группы, удовлетворяющие последнему условию, наз. унимодулярными.
. Этот гомоморфизм тривиален тогда и только тогда, когда левоинвариантная мера Хаара на группе Gявляется одновременно и правоинвариантной. Группы, удовлетворяющие последнему условию, наз. унимодулярными. к-рого определяет автоморфизм умножения на
к-рого определяет автоморфизм умножения на  аддитивной группы тела К. Функция
аддитивной группы тела К. Функция  используется при изучении структуры локально компактных тел.
используется при изучении структуры локально компактных тел.