|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МОДУЛЬЗначение МОДУЛЬ в математической энциклопедии: - абелева группа с кольцом операторов. М. является обобщением (линейного) векторного пространства над полем Кдля случая, когда Кзаменяется нек-рым кольцом. Пусть задано кольцо А. Аддитивная абелева группа Мназ. левым А- модулем, если определено отображение
Если кольцо Аобладает единицей, то обычно требуют дополнительно, чтобы для любого Аналогично определяются правые A-модули; при этом аксиома 3) заменяется условием Простейшие примеры М. (конечные абелевы группы, т. <е. Примеры модулей. 1) Любая абелева группа Мявляется М. над кольцом целых чисел 2) В случае, когда А- поле, понятие унитарного A-модуля в точности эквивалентно понятию линейного векторного пространства над А. 3) Координатное n-мерное векторное пространство V над полем Кможно рассматривать как М. над кольцом 4) Ассоциативное кольцо Аявляется левым Л-мо-дулем. Умножение элементов кольца на элементы М. совпадает с обычным умножением в Л. 5) Дифференциальные формы на гладком многообразии Xснабжены естественной структурой М. над кольцом всех гладких функций на X. 6) С любой абелевой труппой Мсвязано ассоциативное кольцо с единицей End (M)всех эндоморфизмов группы М. Группа Мснабжена естественной структурой End (M)-модуля. Если на Мзадана структура A-модуля для нек-рого кольца A. то отображение Очевидно, что модуль Мможно рассматривать также как М. над факторкольцом G-модули. Пусть G- нек-рая группа. Аддитивная абелева группа Мназ. левым G-модулем, если задано отображение Аналогично можно определить правые G-модули. При Примеры G - модулей. 1) Пусть К- расширение Галуа нек-рого поля кс группой Галуа G. Тогда аддитивная и мультипликативная группы поля Кснабжены естественной структурой G-модуля. Если к- поле алгебраич. чисел, то G-модулями также являются аддитивная группа кольца целых чисел поля K, группа единиц поля К, группа дивизоров и группа классов дивизоров поля К, и т. д. М. над группой Галуа наз. также модулями Галуа. 2) Пусть задано нек-рое расширение абелевой группы М, т. е. точная последовательность групп
где М- абелев нормальный делитель группы Fи G - произвольная группа. Тогда группу Мможно снабдить естественной структурой G-модуля, положив для В тех случаях, когда групповая операция в абелевой группе Мзаписывается мультипликативно (напр., М- мультипликативная группа нек-рого поля), вместо записи gm используют также запись mg, т. е. операторы из группы G записывают как показатели. Пусть задан G-модуль М. Сопоставляя элементу Понятия М. над кольцом и G-модуля тесно связаны. Именно, любой G-модуль Мможно рассматривать как М. над групповым кольцом
где В случае, когда Мявляется K-модулем над нек-рым коммутативным кольцом Ки одновременно G-модулем, причем действие элементов группы G на Мперестановочно с действием элементов К, М можно снабдить структурой KG -модуля, распространяя действие с Gна KG по линейности. Напр., если V- линейное векторное пространство над полем К, то задание структуры KG -модуля на Vэквивалентно заданию представления Gв пространстве V. Используя стандартную инволюцию Модуль над алгеброй Ли. Пусть
для любых Конструкции в теории модулей. Исходя из заданных A-модулей, можно получать новые А-модули при помощи ряда стандартных построений. Так, с любым модулем Мсвязана решетка всех его подмодулей. Напр., если кольцо A рассматривать как левый М. над собой, то его левые подмодули - это в точности левые идеалы кольца А. Ряд важных типов М. определяется в терминах решетки подмодулей. Напр., условие обрыва убывающих (возрастающих) цепей подмодулей определяет артиновы модули( нётеровы модули). Условие отсутствия нетривиальных подмодулей, т. е. подмодулей, отличных от 0 и всего М., выделяет неприводимые модули. Для модуля Ми любого его подмодуля Nфакторгруппу M/N можно снабдить структурой A-модуля. Этот модуль наз. фактормодулем Мпо N. Гомоморфизм A-модулей определяется как гомоморфизм абелевых групп Для любого семейства Для проективной (индуктивной) системы A-модулей проективный (индуктивный) предел этой системы можно естественным образом снабдить структурой A-модуля. Прямое произведение и прямая сумма М. могут рассматриваться как частные случаи понятий проективного и индуктивного пределов. Образующие и соотношения. Пусть X - нек-рое подмножество A-модуля М. Подмодулем, по рожденным множеством X, наз. пересечение всех подмодулей модуля М, содержащих X. Если этот подмодуль совпадает с М, то Xназ. семейством (или системой) образующих модуля М. М., допускающий конечное семейство образующих, наз. конечно порожденным модулем. Напр., в нётеровом кольце любой идеал является конечно порожденным М., прямая сумма конечного числа конечно порожденных М. снова конечно порождена. Любой фактормодуль конечно порожденного М. также конечно порожден. Для построения системы образующих модуля Мчасто оказывается полезной лемма Накаямы: для любого идеала Пусть М- модуль с системой образующих Замена кольца. Существуют стандартные конструкции, позволяющие рассматривать A-модуль Мкак М. над нек-рым другим кольцом. Напр., пусть задан гомоморфизм колец Если модуль М- унитарный A-модуль, и гомоморфизм j переводит единицу в единицу, то Мстанет унитарным B-модулем. Пусть задан нек-рый гомоморфизм колец Категория модулей. Класс всех М. над заданным кольцом Ас гомоморфизмами М. в качестве морфиз-мов образует абелеву категорию, обозначаемую
и
т. е. функтор Ноm контравариантен по первому аргументу и ковариантен по второму. В случае, когда Мили N несет структуру бимодуля, группа Функтор Многие важные типы М. характеризуются в терминах функторов Ноm и М. над данным кольцом Аможно рассматривать с двух точек зрения. 1) Можно изучать М. с точки зрения их внутренней структуры. Основной задачей здесь является полная классификация М., т. е. построение для каждого М. системы инвариантов, характеризующей этот М. с точностью до изоморфизма, и умение по заданному набору инвариантов строить М. с этими инвариантами. Для нек-рых типов колец такое описание возможно. Напр., если М- конечно порожденный М. над групповым кольцом KG конечной группы G, где К- нек-рое поле, характеристика к-рого взаимно проста с порядком G, то Мпредставим в виде конечной прямой суммы неприводимых подмодулей (модуль Мвполне приводим). Это представление определено однозначно с точностью до изоморфизма (сами неприводимые подмодули в общем случае не определяются однозначно). Все неприводимые подмодули также допускают простое описание: все они содержатся в регулярном представлении группы Gи находятся во взаимно однозначном соответствии с неприводимыми характерами этой группы. Также простое описание допускают М. над кольцом главных идеалов и над дедекиндовым кольцом. Именно, любой конечно порожденный модуль Мнад кольцом главных идеалов Аизоморфен конечной прямой сумме М. вида 2) Другой подход к изучению М. состоит в изучении категории A = mod и данного модуля Мкак объекта этой категории. Такое изучение является предметом гомологич. алгебры и алгебраич. K-теории. На этом пути было получено много важных и глубоких результатов. Часто рассматривают М., несущие нек-рую дополнительную структуру. Так рассматриваются градуированные модули, фильтрованные модули, топологические модули, модули с полуторалинейной формой и т. д. Лит.:[1] Бурбаки Н., Алгебра. Модули, кольца, формы, пер. с франц., М., 1966; [2] его же, Коммутативная алгебра, пер. с франц., М., 1971; [3] его же, Группы и алгебры Ли. Алгебры Ли, свободные алгебры Ли и группы Ли, пер. с франц., М., 1976; [4] Ленг С, Алгебра, пер. с англ., М., 1968; [5] Ван дер Варден Б. Л-, Алгебра, пер. с нем., 2 изд., М., 1979; [6] Кострикин А. И., Введение в алгебру, М., 1977; [7] Джекобсон Н., Строение колец, пер. с англ., М., 1961; [8] Херстейн И., Некоммутативные кольца, пер. с англ., М., 1972; [9] Фейс К., Алгебра: кольца, модули и категории, пер. с англ., т. 1-2, М., 1977-79; [10] Картан А., Эйленберг С, Гомологическая алгебра, пер. с англ., М., 1960; [11] Маклейн С, Гомология, пер. с англ., М., 1966; [12] Басе X., Алгебраическая K-теория, пер. с англ., М., 1973; [13] Милнор Дж., Введение в алгебраическую К-теорию, пер. с англ., М., 1974. Л. В. Кузьмин. |
|
|
|

 значение к-рого на паре
значение к-рого на паре  для
для  записывается как am, причем выполняются аксиомы:
записывается как am, причем выполняются аксиомы:
 выполнялось равенство
выполнялось равенство  . М. с этим свойством наз. унитарным, или унитальным.
. М. с этим свойством наз. унитарным, или унитальным.
 Любой правый А-модуль можно рассматривать как левый
Любой правый А-модуль можно рассматривать как левый  -модуль над кольцом
-модуль над кольцом  , антиизоморфным кольцу А, поэтому любому утверждению о правых A-модулях соответствует нек-рое утверждение о левых
, антиизоморфным кольцу А, поэтому любому утверждению о правых A-модулях соответствует нек-рое утверждение о левых  -модулях и наоборот. В случае, когда кольцо Акоммутативно, любой левый A-модулъ можно рассматривать как правый A-модуль, и различие между левыми и правыми М. исчезает. Ниже будут рассматриваться только левые A-модули.
-модулях и наоборот. В случае, когда кольцо Акоммутативно, любой левый A-модулъ можно рассматривать как правый A-модуль, и различие между левыми и правыми М. исчезает. Ниже будут рассматриваться только левые A-модули. -модули) появляются уже у К. Гаусса (C.Gauss) как группы классов бинарных квадратичных форм. Общее понятие М. встречается впервые в 60-80-х гг. 19 в. в работах Р. Дедекинда (R. Dedekind) и Л. Кронекера (L. Kronecker), посвященных арифметике полей алгебраич. чисел и алгебраич. функций. Проводившееся примерно в это же время исследование конечномерных ассоциативных алгебр, и в частности групповых алгебр конечных групп (Б. Пирс, В. Peirce, Ф. Фробениус, F. Frobenius), привело к изучению идеалов нек-рых некоммутативных колец. Первоначально теория М. развивалась преимущественно как теория идеалов нек-рого кольца. Лишь позднее в работах Э. Нётер (Е. Noether) и В. Крулля (W. Krull) было замечено, что многие результаты удобнее формулировать и доказывать в терминах произвольных М., а не только идеалов. Последующее развитие теории М. связано с применением методов и идей теории категорий, в частности методов гомологич. алгебры.
-модули) появляются уже у К. Гаусса (C.Gauss) как группы классов бинарных квадратичных форм. Общее понятие М. встречается впервые в 60-80-х гг. 19 в. в работах Р. Дедекинда (R. Dedekind) и Л. Кронекера (L. Kronecker), посвященных арифметике полей алгебраич. чисел и алгебраич. функций. Проводившееся примерно в это же время исследование конечномерных ассоциативных алгебр, и в частности групповых алгебр конечных групп (Б. Пирс, В. Peirce, Ф. Фробениус, F. Frobenius), привело к изучению идеалов нек-рых некоммутативных колец. Первоначально теория М. развивалась преимущественно как теория идеалов нек-рого кольца. Лишь позднее в работах Э. Нётер (Е. Noether) и В. Крулля (W. Krull) было замечено, что многие результаты удобнее формулировать и доказывать в терминах произвольных М., а не только идеалов. Последующее развитие теории М. связано с применением методов и идей теории категорий, в частности методов гомологич. алгебры. . Для
. Для  и
и  произведение am определяется как результат сложения т а раз.
произведение am определяется как результат сложения т а раз. всех
всех  -матриц с коэффициентами из К. Для
-матриц с коэффициентами из К. Для  и
и 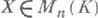 произведение
произведение 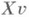 определяется как умножение матрицы Xна столбец координат вектора
определяется как умножение матрицы Xна столбец координат вектора  .
. является эндоморфизмом Мдля любого
является эндоморфизмом Мдля любого  . Сопоставляя элементу
. Сопоставляя элементу  порождаемый им эндоморфизм М, получают гомоморфизм
порождаемый им эндоморфизм М, получают гомоморфизм  кольца
кольца  в
в  . Наоборот, любой гомоморфизм
. Наоборот, любой гомоморфизм  определяет на Мструктуру A-модуля. Таким образом, задание структуры A-модуля на абелевой группе Мравносильно заданию гомоморфизма
определяет на Мструктуру A-модуля. Таким образом, задание структуры A-модуля на абелевой группе Мравносильно заданию гомоморфизма  . Такой гомоморфизм наз. также представлением кольца A, а Мназ. модулем представления. С любым представлением
. Такой гомоморфизм наз. также представлением кольца A, а Мназ. модулем представления. С любым представлением  связан двусторонний идеал
связан двусторонний идеал  , состоящий из элементов
, состоящий из элементов  таких, что am=0 для всех
таких, что am=0 для всех  . Этот идеал наз. аннулятором модуля М. В случае, когда
. Этот идеал наз. аннулятором модуля М. В случае, когда  представление наз. точным,
представление наз. точным, - точным модулем.
- точным модулем.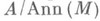 . В частности, хотя определение М. и не предполагает ассоциативности кольца A, кольцо
. В частности, хотя определение М. и не предполагает ассоциативности кольца A, кольцо  всегда ассоциативно. Поэтому в большинстве случаев достаточно ограничиться рассмотрением М. над ассоциативными кольцами. Ниже, везде, где не оговорено противное, кольцо A будет предполагаться ассоциативным.
всегда ассоциативно. Поэтому в большинстве случаев достаточно ограничиться рассмотрением М. над ассоциативными кольцами. Ниже, везде, где не оговорено противное, кольцо A будет предполагаться ассоциативным. , значение к-рого на паре
, значение к-рого на паре  , где
, где  , записывается как gm, причем для любого
, записывается как gm, причем для любого  отображение
отображение  является эндоморфизмом группы М, для любых
является эндоморфизмом группы М, для любых  ,
,  ,
,  и для всех
и для всех  где 1 - единица группы G. Для любого
где 1 - единица группы G. Для любого  отображение
отображение  является автоморфизмом группы М.
является автоморфизмом группы М. любой правый G-модуль будет левым G-модулем.
любой правый G-модуль будет левым G-модулем.
 где
где  - нек-рый прообраз элемента gв группе F.
- нек-рый прообраз элемента gв группе F. автоморфизм
автоморфизм  группы М, получают гомоморфизм группы
группы М, получают гомоморфизм группы  в группу обратимых элементов кольца
в группу обратимых элементов кольца  . Наоборот, любой гомоморфизм группы G в группу обратимых элементов кольца End (М) задает на Мструктуру G-модуля.
. Наоборот, любой гомоморфизм группы G в группу обратимых элементов кольца End (М) задает на Мструктуру G-модуля. , если распространить действие группы
, если распространить действие группы  на
на  по линейности, т. е. положить
по линейности, т. е. положить
 Наоборот, если на Мзадана структура унитарного
Наоборот, если на Мзадана структура унитарного  G-модуля, то Мможно рассматривать как G-модуль.
G-модуля, то Мможно рассматривать как G-модуль. в группе G, любой левый G-модуль Мможно превратить в правый G-модуль, положив
в группе G, любой левый G-модуль Мможно превратить в правый G-модуль, положив  Аналогично, любой правый G-модуль можно превратить в левый G-модуль.
Аналогично, любой правый G-модуль можно превратить в левый G-модуль. - алгебра Ли над коммутативным кольцом Ки М- нек-рый K-мо-дуль. Задание структуры
- алгебра Ли над коммутативным кольцом Ки М- нек-рый K-мо-дуль. Задание структуры  -модуля на Мсостоит в задании K-эндоморфизма
-модуля на Мсостоит в задании K-эндоморфизма  группы Мдля каждого
группы Мдля каждого  , причем требуется выполнение аксиомы
, причем требуется выполнение аксиомы
 . Это определение отличается от данного ранее определения A-модуля. Задание на Мструктуры
. Это определение отличается от данного ранее определения A-модуля. Задание на Мструктуры  -модуля равносильно заданию K-гомоморфизма
-модуля равносильно заданию K-гомоморфизма  в алгебру Ли кольца End (М). Модуль Мнад алгеброй Ли
в алгебру Ли кольца End (М). Модуль Мнад алгеброй Ли  можно рассматривать также как М. в обычном смысле над универсальной обертывающей алгеброй алгебры
можно рассматривать также как М. в обычном смысле над универсальной обертывающей алгеброй алгебры 
 , перестановочный с умножением на элементы кольца А, т. <е. удовлетворяющий условию
, перестановочный с умножением на элементы кольца А, т. <е. удовлетворяющий условию  для всех
для всех  Если заданы два гомоморфизма
Если заданы два гомоморфизма  , то их сумма, определяемая формулой
, то их сумма, определяемая формулой 
 , снова будет гомоморфизмом А-модулей. Это сложение задает на множестве
, снова будет гомоморфизмом А-модулей. Это сложение задает на множестве  всех гомоморфизмов модуля Мв Nстроение абелевой группы. Для любого гомоморфизма
всех гомоморфизмов модуля Мв Nстроение абелевой группы. Для любого гомоморфизма  определены подмодули
определены подмодули  и
и  , а также фактормодули
, а также фактормодули  (коядро f) и
(коядро f) и  (кообраз f). М. Imf и Coim f канонически изоморфны, поэтому их обычно отождествляют. Напр., для любого левого идеала f кольца Аопределен фактормодуль A/J. М. A/J неприводим тогда и только тогда, когда J - максимальный левый идеал. Если М- иек-рый неприводимый A-модуль, не аннулируемый кольцом А, то Мизоморфен М. A/J для нек-рого максимального левого идеала J.
(кообраз f). М. Imf и Coim f канонически изоморфны, поэтому их обычно отождествляют. Напр., для любого левого идеала f кольца Аопределен фактормодуль A/J. М. A/J неприводим тогда и только тогда, когда J - максимальный левый идеал. Если М- иек-рый неприводимый A-модуль, не аннулируемый кольцом А, то Мизоморфен М. A/J для нек-рого максимального левого идеала J. , где
, где  пробегает нек-рое множество индексов J, в категории A-модулей существуют прямая сумма и прямое произведение семейства
пробегает нек-рое множество индексов J, в категории A-модулей существуют прямая сумма и прямое произведение семейства  . При этом элементы прямого произведения
. При этом элементы прямого произведения  можно интерпретировать как векторы
можно интерпретировать как векторы  , компоненты к-рых заиндексированы множеством J, причем для каждого индекса
, компоненты к-рых заиндексированы множеством J, причем для каждого индекса  . Сложение таких векторов и умножение их на элементы кольца определяются покомпонентно. Прямую сумму
. Сложение таких векторов и умножение их на элементы кольца определяются покомпонентно. Прямую сумму  семейства
семейства  можно интерпретировать как подмодуль прямого произведения, состоящий из векторов, у к-рых все компоненты, кроме конечного числа, равны нулю.
можно интерпретировать как подмодуль прямого произведения, состоящий из векторов, у к-рых все компоненты, кроме конечного числа, равны нулю. , содержащегося в радикале кольца А, из условия
, содержащегося в радикале кольца А, из условия  следует М=0. В частности, в условиях леммы Накаямы элементы
следует М=0. В частности, в условиях леммы Накаямы элементы  являются системой образующих для М, если их образы порождают модуль
являются системой образующих для М, если их образы порождают модуль  Это соображение особенно часто используется в случае, когда A - локальное кольцо и
Это соображение особенно часто используется в случае, когда A - локальное кольцо и  - максимальный идеал в A.
- максимальный идеал в A. Тогда отображение
Тогда отображение  определяет эпиморфизм
определяет эпиморфизм  свободного A-модуля Fс образующими
свободного A-модуля Fс образующими  на М(М. Fможно определить как множество формальных конечных сумм
на М(М. Fможно определить как множество формальных конечных сумм  отображение
отображение  распространяется с образующих на элементы М. Fпо линейности). Элементы М.
распространяется с образующих на элементы М. Fпо линейности). Элементы М. наз. соотношениями между образующими
наз. соотношениями между образующими  модуля М. Если модуль Мможно представить как фактормодуль конечно порожденного свободного М. Fтак, чтобы М. соотношений Rтакже был конечно порожден, что Мназ. конечно представимым модулем. Напр., над нётеровым кольцом A любой конечно порожденный М. конечно представим. В общем случае конечная представимость не следует из конечной порожденности.
модуля М. Если модуль Мможно представить как фактормодуль конечно порожденного свободного М. Fтак, чтобы М. соотношений Rтакже был конечно порожден, что Мназ. конечно представимым модулем. Напр., над нётеровым кольцом A любой конечно порожденный М. конечно представим. В общем случае конечная представимость не следует из конечной порожденности. . Тогда, полагая
. Тогда, полагая 
 , можно рассматривать Мкак В-модуль.
, можно рассматривать Мкак В-модуль. и A-модуль М. Тогда Вможно снабдить структурой ( В, A )-модуля, полагая
и A-модуль М. Тогда Вможно снабдить структурой ( В, A )-модуля, полагая  для
для  и можно рассмотреть левый B-модуль
и можно рассмотреть левый B-модуль  . Говорят, что этот М. получен из M расширением скаляров.
. Говорят, что этот М. получен из M расширением скаляров. Из функторов, определенных на этой категории, наиболее важны функторы Нот (гомоморфизмы) и
Из функторов, определенных на этой категории, наиболее важны функторы Нот (гомоморфизмы) и  (тензорное произведение). Функтор Ноm принимает значения в категории абелевых групп и сопоставляет паре A-модулей М, N, группу
(тензорное произведение). Функтор Ноm принимает значения в категории абелевых групп и сопоставляет паре A-модулей М, N, группу  . Для
. Для  очевидным образом определяются отображения
очевидным образом определяются отображения

 обладает дополнительной модульной структурой. Если Nесть (А, B)-модуль, то
обладает дополнительной модульной структурой. Если Nесть (А, B)-модуль, то  - правый B-модуль, а если Месть ( А, В )-бимодуль, то
- правый B-модуль, а если Месть ( А, В )-бимодуль, то  - левый В-модуль.
- левый В-модуль. ставит в соответствие паре М, N, где М - правый A-модуль, a N - левый A-модуль, тензорное произведение
ставит в соответствие паре М, N, где М - правый A-модуль, a N - левый A-модуль, тензорное произведение  модулей Ми Nнад кольцом А. Этот функтор принимает значения в категории абелевых групп и ковариантен как по М, так и по N. В случае, когда Мили N- бимодули, группу
модулей Ми Nнад кольцом А. Этот функтор принимает значения в категории абелевых групп и ковариантен как по М, так и по N. В случае, когда Мили N- бимодули, группу  можно снабдить дополнительной структурой. Именно, если Месть (В, A)-модуль, то
можно снабдить дополнительной структурой. Именно, если Месть (В, A)-модуль, то  есть В-модуль, а если Nесть ( А, В )-бимодуль, то
есть В-модуль, а если Nесть ( А, В )-бимодуль, то  - правый В-модуль. Изучение функторов Ноm и
- правый В-модуль. Изучение функторов Ноm и  , а также их производных функторов является одной из основных задач гомологич. алгебры.
, а также их производных функторов является одной из основных задач гомологич. алгебры. . Так, проективный модуль М определяется требованием, чтобы функтор
. Так, проективный модуль М определяется требованием, чтобы функтор  (от X)был точным. Аналогично, инъективный модуль N определяется требованием точности
(от X)был точным. Аналогично, инъективный модуль N определяется требованием точности  (от X). Плоский модуль М определяется требованием точности функтора
(от X). Плоский модуль М определяется требованием точности функтора 
 , где
, где  - нек-рые идеалы кольца А(возможно, нулевые), причем
- нек-рые идеалы кольца А(возможно, нулевые), причем 
 и идеалы
и идеалы  однозначно определяются последним условием. Таким образом, набор инвариантов
однозначно определяются последним условием. Таким образом, набор инвариантов  полностью определяет модуль М. Если М- конечно порожденный М. над дедекиндовым кольцом А, то
полностью определяет модуль М. Если М- конечно порожденный М. над дедекиндовым кольцом А, то  где
где  - периодич. М., а М 2- М. без кручения (выбор модуля
- периодич. М., а М 2- М. без кручения (выбор модуля  не однозначен). Модуль
не однозначен). Модуль  аннулируется нек-рым идеалом
аннулируется нек-рым идеалом  кольца Аи, следовательно, является М. над кольцом главных идеалов
кольца Аи, следовательно, является М. над кольцом главных идеалов  и допускает описание, указанное выше, а модуль
и допускает описание, указанное выше, а модуль  представим в виде
представим в виде  - нек-рый идеал А, а
- нек-рый идеал А, а  - прямая сумма праз. Модуль М 1 с точностью до изоморфизма однозначно определяется двумя инвариантами: числом пи классом идеала
- прямая сумма праз. Модуль М 1 с точностью до изоморфизма однозначно определяется двумя инвариантами: числом пи классом идеала  в группе классов идеалов.
в группе классов идеалов.