"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МОДУЛЕЙ ТЕОРИЯ
Значение МОДУЛЕЙ ТЕОРИЯ в математической энциклопедии:
- теория, изучающая непрерывные семейства объектов алгебраич. геометрии.
Пусть А- класс объектов алгебраич. геометрии (многообразий, схем, векторных расслоений и т. п.), на к-ром задано нек-рое отношение эквивалентности R. Основная задача классификации (описания множества классов A/R )состоит из следующих двух частей: 1) описание дискретных инвариантов, к-рые обычно позволяют разбить A/R в счетное число подмножеств, объекты к-рых уже непрерывно зависят от параметров; 2) задание и изучение алгебро-геометрич. структур на множествах параметров. Вторая часть составляет содержание М. т.
М. т. возникла при изучении эллиптич. функций: существует непрерывное семейство различных полей эллиптич. функций (или их моделей - неизоморфных эллиптич. кривых над  ), параметризованное комплексными числами. Б. Риман (В. Riemann), к-рому принадлежит и сам термин "модули", показал, что поля алгебраич. функций над
), параметризованное комплексными числами. Б. Риман (В. Riemann), к-рому принадлежит и сам термин "модули", показал, что поля алгебраич. функций над  (или их моделей - компактных римановых поверхностей) рода
(или их моделей - компактных римановых поверхностей) рода  зависят от 3g-3 непрерывных комплексных параметров - модулей.
зависят от 3g-3 непрерывных комплексных параметров - модулей.
Основные понятия М. т. Пусть S- нек-рая схема (комплексное или алгебраич. пространство). Семейство объектов, параметризованных схемой S(или, как часто говорят, "над 5", или "с базой S"),- это набор объектов

снабженный дополнительной структурой, согласованной со структурой базы S. Эта структура в каждом конкретном случае задается явно. Функтор семейств - это контравариантный функтор  из категории схем (или пространств) в категорию множеств, определяемый следующим образом:
из категории схем (или пространств) в категорию множеств, определяемый следующим образом:  - множество классов изоморфных семейств над S. Каждому морфизму
- множество классов изоморфных семейств над S. Каждому морфизму  сопоставляется отображение
сопоставляется отображение  посредством взятия индуцированного семейства.
посредством взятия индуцированного семейства.
Пусть М- объект в категории схем (комплексных или алгебраич. пространств) и  - функтор точек в этой категории, т. е.
- функтор точек в этой категории, т. е.  . Если функтор семейств
. Если функтор семейств  представим, т. е.
представим, т. е. для нек-рого М, то существует универсальное семейство с базой
для нек-рого М, то существует универсальное семейство с базой  , и Мназ. тонкой схемой (соответственно тонким комплексным или алгебраическим пространством) модулей. Функтор
, и Мназ. тонкой схемой (соответственно тонким комплексным или алгебраическим пространством) модулей. Функтор  представим в очень немногих случаях, в связи с чем было введено также понятие грубой схемы модулей; Мназ. грубой схемой модулей, если существует морфизм функторов
представим в очень немногих случаях, в связи с чем было введено также понятие грубой схемы модулей; Мназ. грубой схемой модулей, если существует морфизм функторов  , обладающий свойствами: а) если S=SpecK=pt- одна точка (где К- алгебраически замкнутое поле), то отображение
, обладающий свойствами: а) если S=SpecK=pt- одна точка (где К- алгебраически замкнутое поле), то отображение  биективно, иначе говоря, множество геометрич. точек схемы Мнаходится в естественном взаимно однозначном соответствии с множеством классов эквивалентности параметризуемых объектов; б) для каждой схемы N и морфизма функторов
биективно, иначе говоря, множество геометрич. точек схемы Мнаходится в естественном взаимно однозначном соответствии с множеством классов эквивалентности параметризуемых объектов; б) для каждой схемы N и морфизма функторов 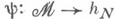 существует единственный морфизм
существует единственный морфизм  такой, что
такой, что  . Аналогично определяются грубая схема комплексного и алгебраического пространств модулей.
. Аналогично определяются грубая схема комплексного и алгебраического пространств модулей.
Грубая схема модулей хотя и параметризует однозначно классы изучаемых объектов с заданными дискретными инвариантами, но естественное семейство над ней не обладает (в отличие от семейства над тонкой схемой модулей) сильным свойством универсальности.
Грубая схема (пространство) модулей существует уже в достаточно большом числе случаев.
Примеры. 1)Модули алгебраических кривых. Пусть  (соответственно
(соответственно  ) - множество классов изоморфных проективных неособых кривых (соответственно стабильных кривых) рода
) - множество классов изоморфных проективных неособых кривых (соответственно стабильных кривых) рода  над алгебраически замкнутым полем К. Семейство над S- это гладкий (плоский) собственный морфизм схем
над алгебраически замкнутым полем К. Семейство над S- это гладкий (плоский) собственный морфизм схем  , слоями к-рого являются гладкие (стабильные) кривые рода g. Тогда существует грубая (но не тонкая) схема модулей
, слоями к-рого являются гладкие (стабильные) кривые рода g. Тогда существует грубая (но не тонкая) схема модулей  (соответственно
(соответственно  ), являющаяся квазипроективным (проективным) неприводимым и нормальным многообразием над К. (см. [3], [5], [6]).
), являющаяся квазипроективным (проективным) неприводимым и нормальным многообразием над К. (см. [3], [5], [6]).
2) Модули алгебраических кривых с якобиевой жесткостью. Пусть  - гладкое семейство проективных кривых (соответственно плоское семейство стабильных кривых) рода
- гладкое семейство проективных кривых (соответственно плоское семейство стабильных кривых) рода  , п- целое число, обратимое на
, п- целое число, обратимое на  , и
, и  - первый прямой образ постоянного пучка
- первый прямой образ постоянного пучка  в этальной топологии. Тогда
в этальной топологии. Тогда  локально свободен, имеет ранг
локально свободен, имеет ранг  и снабжен локально невырожденной симплектич. формой со значением в
и снабжен локально невырожденной симплектич. формой со значением в  , с точностью до обратимого элемента из
, с точностью до обратимого элемента из  . Якобиева структура уровня и на X- это задание симплектич. изоморфизма
. Якобиева структура уровня и на X- это задание симплектич. изоморфизма 
Пусть  (соответственно
(соответственно  ) - функтор семейств гладких (стабильных) кривых рода
) - функтор семейств гладких (стабильных) кривых рода  с якобиевой жесткостью уровня п. Тогда при
с якобиевой жесткостью уровня п. Тогда при  функтор
функтор  (соответственно
(соответственно  ) представим квазипроективной (проективной) схемой
) представим квазипроективной (проективной) схемой  (соответственно
(соответственно  ) над
) над  , где
, где  - первообразный корень n-й степени из 1, т. е. существует тонкая схема модулей
- первообразный корень n-й степени из 1, т. е. существует тонкая схема модулей  (соответственно
(соответственно  ) для гладких (стабильных) кривых рода
) для гладких (стабильных) кривых рода  над полем характеристики взаимно простой с я, снабженных якобиевой жесткостью уровня п. Для достаточно больших и схема
над полем характеристики взаимно простой с я, снабженных якобиевой жесткостью уровня п. Для достаточно больших и схема  является гладкой [5].
является гладкой [5].
3) Поляризованные алгебраические многообразия. Поляризованным семейством наз. пара  , где
, где  - гладкое семейство многообразий, т. е. гладкий собственный морфизм
- гладкое семейство многообразий, т. е. гладкий собственный морфизм  , а
, а  - класс относительно обильного обратимого пучка .
- класс относительно обильного обратимого пучка . в
в  по модулю
по модулю 
 , где
, где  - относительная схема Пикара, а
- относительная схема Пикара, а  - ее связная компонента нулевого сечения.
- ее связная компонента нулевого сечения.
В этом случае строится функтор поляризованных семейств  с заданным многочленом Гильберта h.
с заданным многочленом Гильберта h.
Без дополнительных ограничений этот функтор не представим. Существование грубого пространства модулей известно (1982) лишь в отдельных случаях. Для поляризованных алгебраич. многообразий также существует понятие жесткости уровня п.
4) Векторные расслоения. Пусть  - множество классов векторных расслоений ранга пна алгебраич. многообразии X. Семейство над S- это векторное расслоение Ена
- множество классов векторных расслоений ранга пна алгебраич. многообразии X. Семейство над S- это векторное расслоение Ена  . Грубое пространство модулей
. Грубое пространство модулей  существует здесь как нормальнее проективное многообразие для полустабильных векторных расслоений ранга пи степени dна неособой проективной алгебраич. кривой Xнад алгебраически замкнутым полем К. Стабильные векторные расслоения в
существует здесь как нормальнее проективное многообразие для полустабильных векторных расслоений ранга пи степени dна неособой проективной алгебраич. кривой Xнад алгебраически замкнутым полем К. Стабильные векторные расслоения в  параметризуются открытым гладким подмногообразием
параметризуются открытым гладким подмногообразием  . Если dи n взаимно просты, то
. Если dи n взаимно просты, то  . Аналогичные результаты получены и для стабильных векторных расслоений на алгебраич. поверхности. Более того, в этом случае существует тонкая схема модулей (см. [7], [10] - [14]).
. Аналогичные результаты получены и для стабильных векторных расслоений на алгебраич. поверхности. Более того, в этом случае существует тонкая схема модулей (см. [7], [10] - [14]).
Локальная и глобальная теории. Локальная теория возникла как теория деформаций комплексных структур (см. Деформация1) и 2)). Основными методами глобальной теории являются теория представимых функторов и геометрич. теория инвариантов, теория алгебраич. стеков и алгебраизация формальных модулей.
Метод построения глобального пространства модулей восходит к классической инвариантов теории. Он заключается в следующем. Строится достаточно большое семейство  , содержащее представителей всех классов эквивалентности изучаемых объектов, причем такое, что отношение эквивалентности на Нсводится к действию алгебраич. группы G. Затем развивается теория действия алгебраич. групп на алгебраич. многообразиях (схемах, пространствах) с целью выяснения условий существования фактора H/G в соответствующей категории. Основным инструментом построения семейства
, содержащее представителей всех классов эквивалентности изучаемых объектов, причем такое, что отношение эквивалентности на Нсводится к действию алгебраич. группы G. Затем развивается теория действия алгебраич. групп на алгебраич. многообразиях (схемах, пространствах) с целью выяснения условий существования фактора H/G в соответствующей категории. Основным инструментом построения семейства  является теория Гильберта схем. При таком подходе трудности построения семейства
является теория Гильберта схем. При таком подходе трудности построения семейства  сводятся к проблеме одновременного погружения изучаемых объектов в проективное пространство. Важным результатом о возможности такого одновременного погружения является теорема Мацусаки. Трудной проблемой остается и проблема существования фактора H/G. Имеются понятия категорного и геометрич. факторов. Конструкция грубого пространства модулей сводится к задаче о существовании геометрич. фактора, при этом используется понятие стабильности точек, соответствующее понятию орбиты общего положения. Результаты одействиях редуктивных групп на алгебраич. многообразиях над полями характеристики 0 распространяются и на случай полей характеристики р>0.
сводятся к проблеме одновременного погружения изучаемых объектов в проективное пространство. Важным результатом о возможности такого одновременного погружения является теорема Мацусаки. Трудной проблемой остается и проблема существования фактора H/G. Имеются понятия категорного и геометрич. факторов. Конструкция грубого пространства модулей сводится к задаче о существовании геометрич. фактора, при этом используется понятие стабильности точек, соответствующее понятию орбиты общего положения. Результаты одействиях редуктивных групп на алгебраич. многообразиях над полями характеристики 0 распространяются и на случай полей характеристики р>0.
Другой подход к глобальной М. т.- метод алгебраич. стеков, т. е. метод глобализации локальной теории деформаций. Первый шаг в исследовании представимости глобального функтора семейств при таком подходе - установление алгебраизуемости формальной версальной деформации для каждого объекта Х о. Трудностью для построения глобального пространства модулей является то, что не всегда факторизация базы семейства по отношению эквивалентности будет отделимым пространством. В таких случаях заменой объекта, представляющего функтор  , служит алгебраич. стек, изучение свойств к-рого позволяет получить нек-рую информацию о пространстве модулей. Один из подходов к глобальной М. т. над
, служит алгебраич. стек, изучение свойств к-рого позволяет получить нек-рую информацию о пространстве модулей. Один из подходов к глобальной М. т. над  - это теория отображения периодов. Основным объектом здесь является классифицирующее пространство Dполяризованных Ходжа структур веса кдля заданных чисел Ходжа. Для семейства
- это теория отображения периодов. Основным объектом здесь является классифицирующее пространство Dполяризованных Ходжа структур веса кдля заданных чисел Ходжа. Для семейства  поляризованных алгебраич. многообразий над
поляризованных алгебраич. многообразий над  периоды определяют отображение Sв соответствующее классифицирующее пространство Dструктур Ходжа. Проблема модулей сводится к изучению условий биективности отображений периодов. Наличие локальной (глобальной) инъ-ективности для отображения периодов - это т. н. локальная (глобальная) проблема Торелли. На этом пути существование грубых пространств модулей доказано для кривых, абелевых многообразий и КЗ-поверхностей.
периоды определяют отображение Sв соответствующее классифицирующее пространство Dструктур Ходжа. Проблема модулей сводится к изучению условий биективности отображений периодов. Наличие локальной (глобальной) инъ-ективности для отображения периодов - это т. н. локальная (глобальная) проблема Торелли. На этом пути существование грубых пространств модулей доказано для кривых, абелевых многообразий и КЗ-поверхностей.
Задача компактификации многообразия модулей Мзаключается в нахождении естественного и полного (проективного или компактного в теории над полем  ) многообразия
) многообразия  , содержащего Мв качестве плотного открытого подмножества, а также в описании и геометрич. интерпретации границы
, содержащего Мв качестве плотного открытого подмножества, а также в описании и геометрич. интерпретации границы  . В примере 1) естественной компактификацией грубого многообразия модулей
. В примере 1) естественной компактификацией грубого многообразия модулей  кривых рода
кривых рода  служит проективное многообразие модулей
служит проективное многообразие модулей  стабильных кривых. В примере 4) многообразие стабильных векторных расслоений ранга пи степени dна алгсбраич. кривой само является проективным и гладким, если (d, я)=1. Для поляризованных абелевых многообразий над
стабильных кривых. В примере 4) многообразие стабильных векторных расслоений ранга пи степени dна алгсбраич. кривой само является проективным и гладким, если (d, я)=1. Для поляризованных абелевых многообразий над  известны несколько способов компактификации многообразий модулей.
известны несколько способов компактификации многообразий модулей.
Лит.:[1] Artin M., Algebraization of formal moduli I. Global Analysis, Tokyo, 1969, p. 21-71; [2] eго же, "Invent, math.". 1974, v. 27, p. 165 - 89; [3] Делинь П., Mамфорд Д., "Математика", 1972, т. 16, .№ 3, с. 13-53; [4] Дьёдонне Ж., Керрол Дж., Мамфорд Д., Геометрическая теория инвариантов, пер. с англ., М., 1974; [5] Mumford D., Geometric invariant theory, В.- [а. <о.], 1965; [6] его же, "L'enseignement math.", 1977, v. 23; [7] Gieseker D.. "Invent, math.", 1977, v. 43, p. 233-82; [8] eго же, "Ann. Math.", 1977, v. 106, p. 45-60; [9] Matsusakа Т., "Amer. J. Math.", 1972, v. 94, №4, p. 1027-77; [10] Newstead P. E., Lectures on introduction to moduli problems and orbit spaces. В.-[a.о.], 1978; [11] Okonek C, Sсheider M., Spindler H.. Vector budles on complex projective spaces, Boston, 1980; [12] Popp H., Moduli theory and classification theory of algebraic varieties, В.-[a. o.], 1977; [13] Seshadri С S., "Ann. Math.", 1967, v. 85, p. 302 - 36; [14] Тюрин А. Н., "Успехи матем. наук", 1974, т. 29, в. 6, с. 59 - 88.
В. А. Псковских.

 ), параметризованное комплексными числами. Б. Риман (В. Riemann), к-рому принадлежит и сам термин "модули", показал, что поля алгебраич. функций над
), параметризованное комплексными числами. Б. Риман (В. Riemann), к-рому принадлежит и сам термин "модули", показал, что поля алгебраич. функций над  (или их моделей - компактных римановых поверхностей) рода
(или их моделей - компактных римановых поверхностей) рода  зависят от 3g-3 непрерывных комплексных параметров - модулей.
зависят от 3g-3 непрерывных комплексных параметров - модулей.
 из категории схем (или пространств) в категорию множеств, определяемый следующим образом:
из категории схем (или пространств) в категорию множеств, определяемый следующим образом:  - множество классов изоморфных семейств над S. Каждому морфизму
- множество классов изоморфных семейств над S. Каждому морфизму  сопоставляется отображение
сопоставляется отображение  посредством взятия индуцированного семейства.
посредством взятия индуцированного семейства. - функтор точек в этой категории, т. е.
- функтор точек в этой категории, т. е.  . Если функтор семейств
. Если функтор семейств  представим, т. е.
представим, т. е. для нек-рого М, то существует универсальное семейство с базой
для нек-рого М, то существует универсальное семейство с базой  , и Мназ. тонкой схемой (соответственно тонким комплексным или алгебраическим пространством) модулей. Функтор
, и Мназ. тонкой схемой (соответственно тонким комплексным или алгебраическим пространством) модулей. Функтор  представим в очень немногих случаях, в связи с чем было введено также понятие грубой схемы модулей; Мназ. грубой схемой модулей, если существует морфизм функторов
представим в очень немногих случаях, в связи с чем было введено также понятие грубой схемы модулей; Мназ. грубой схемой модулей, если существует морфизм функторов  , обладающий свойствами: а) если S=SpecK=pt- одна точка (где К- алгебраически замкнутое поле), то отображение
, обладающий свойствами: а) если S=SpecK=pt- одна точка (где К- алгебраически замкнутое поле), то отображение  биективно, иначе говоря, множество геометрич. точек схемы Мнаходится в естественном взаимно однозначном соответствии с множеством классов эквивалентности параметризуемых объектов; б) для каждой схемы N и морфизма функторов
биективно, иначе говоря, множество геометрич. точек схемы Мнаходится в естественном взаимно однозначном соответствии с множеством классов эквивалентности параметризуемых объектов; б) для каждой схемы N и морфизма функторов 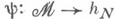 существует единственный морфизм
существует единственный морфизм  такой, что
такой, что  . Аналогично определяются грубая схема комплексного и алгебраического пространств модулей.
. Аналогично определяются грубая схема комплексного и алгебраического пространств модулей. (соответственно
(соответственно  ) - множество классов изоморфных проективных неособых кривых (соответственно стабильных кривых) рода
) - множество классов изоморфных проективных неособых кривых (соответственно стабильных кривых) рода  над алгебраически замкнутым полем К. Семейство над S- это гладкий (плоский) собственный морфизм схем
над алгебраически замкнутым полем К. Семейство над S- это гладкий (плоский) собственный морфизм схем  , слоями к-рого являются гладкие (стабильные) кривые рода g. Тогда существует грубая (но не тонкая) схема модулей
, слоями к-рого являются гладкие (стабильные) кривые рода g. Тогда существует грубая (но не тонкая) схема модулей  (соответственно
(соответственно  ), являющаяся квазипроективным (проективным) неприводимым и нормальным многообразием над К. (см. [3], [5], [6]).
), являющаяся квазипроективным (проективным) неприводимым и нормальным многообразием над К. (см. [3], [5], [6]). - гладкое семейство проективных кривых (соответственно плоское семейство стабильных кривых) рода
- гладкое семейство проективных кривых (соответственно плоское семейство стабильных кривых) рода  , п- целое число, обратимое на
, п- целое число, обратимое на  , и
, и  - первый прямой образ постоянного пучка
- первый прямой образ постоянного пучка  в этальной топологии. Тогда
в этальной топологии. Тогда  локально свободен, имеет ранг
локально свободен, имеет ранг  и снабжен локально невырожденной симплектич. формой со значением в
и снабжен локально невырожденной симплектич. формой со значением в  , с точностью до обратимого элемента из
, с точностью до обратимого элемента из  . Якобиева структура уровня и на X- это задание симплектич. изоморфизма
. Якобиева структура уровня и на X- это задание симплектич. изоморфизма 
 (соответственно
(соответственно  ) - функтор семейств гладких (стабильных) кривых рода
) - функтор семейств гладких (стабильных) кривых рода  с якобиевой жесткостью уровня п. Тогда при
с якобиевой жесткостью уровня п. Тогда при  функтор
функтор  (соответственно
(соответственно  ) представим квазипроективной (проективной) схемой
) представим квазипроективной (проективной) схемой  (соответственно
(соответственно  ) над
) над  , где
, где  - первообразный корень n-й степени из 1, т. е. существует тонкая схема модулей
- первообразный корень n-й степени из 1, т. е. существует тонкая схема модулей  (соответственно
(соответственно  ) для гладких (стабильных) кривых рода
) для гладких (стабильных) кривых рода  над полем характеристики взаимно простой с я, снабженных якобиевой жесткостью уровня п. Для достаточно больших и схема
над полем характеристики взаимно простой с я, снабженных якобиевой жесткостью уровня п. Для достаточно больших и схема  является гладкой [5].
является гладкой [5]. , где
, где  - гладкое семейство многообразий, т. е. гладкий собственный морфизм
- гладкое семейство многообразий, т. е. гладкий собственный морфизм  , а
, а  - класс относительно обильного обратимого пучка .
- класс относительно обильного обратимого пучка . в
в  по модулю
по модулю 
 , где
, где  - относительная схема Пикара, а
- относительная схема Пикара, а  - ее связная компонента нулевого сечения.
- ее связная компонента нулевого сечения. с заданным многочленом Гильберта h.
с заданным многочленом Гильберта h. - множество классов векторных расслоений ранга пна алгебраич. многообразии X. Семейство над S- это векторное расслоение Ена
- множество классов векторных расслоений ранга пна алгебраич. многообразии X. Семейство над S- это векторное расслоение Ена  . Грубое пространство модулей
. Грубое пространство модулей  существует здесь как нормальнее проективное многообразие для полустабильных векторных расслоений ранга пи степени dна неособой проективной алгебраич. кривой Xнад алгебраически замкнутым полем К. Стабильные векторные расслоения в
существует здесь как нормальнее проективное многообразие для полустабильных векторных расслоений ранга пи степени dна неособой проективной алгебраич. кривой Xнад алгебраически замкнутым полем К. Стабильные векторные расслоения в  параметризуются открытым гладким подмногообразием
параметризуются открытым гладким подмногообразием  . Если dи n взаимно просты, то
. Если dи n взаимно просты, то  . Аналогичные результаты получены и для стабильных векторных расслоений на алгебраич. поверхности. Более того, в этом случае существует тонкая схема модулей (см. [7], [10] - [14]).
. Аналогичные результаты получены и для стабильных векторных расслоений на алгебраич. поверхности. Более того, в этом случае существует тонкая схема модулей (см. [7], [10] - [14]). , содержащее представителей всех классов эквивалентности изучаемых объектов, причем такое, что отношение эквивалентности на Нсводится к действию алгебраич. группы G. Затем развивается теория действия алгебраич. групп на алгебраич. многообразиях (схемах, пространствах) с целью выяснения условий существования фактора H/G в соответствующей категории. Основным инструментом построения семейства
, содержащее представителей всех классов эквивалентности изучаемых объектов, причем такое, что отношение эквивалентности на Нсводится к действию алгебраич. группы G. Затем развивается теория действия алгебраич. групп на алгебраич. многообразиях (схемах, пространствах) с целью выяснения условий существования фактора H/G в соответствующей категории. Основным инструментом построения семейства  является теория Гильберта схем. При таком подходе трудности построения семейства
является теория Гильберта схем. При таком подходе трудности построения семейства  сводятся к проблеме одновременного погружения изучаемых объектов в проективное пространство. Важным результатом о возможности такого одновременного погружения является теорема Мацусаки. Трудной проблемой остается и проблема существования фактора H/G. Имеются понятия категорного и геометрич. факторов. Конструкция грубого пространства модулей сводится к задаче о существовании геометрич. фактора, при этом используется понятие стабильности точек, соответствующее понятию орбиты общего положения. Результаты одействиях редуктивных групп на алгебраич. многообразиях над полями характеристики 0 распространяются и на случай полей характеристики р>0.
сводятся к проблеме одновременного погружения изучаемых объектов в проективное пространство. Важным результатом о возможности такого одновременного погружения является теорема Мацусаки. Трудной проблемой остается и проблема существования фактора H/G. Имеются понятия категорного и геометрич. факторов. Конструкция грубого пространства модулей сводится к задаче о существовании геометрич. фактора, при этом используется понятие стабильности точек, соответствующее понятию орбиты общего положения. Результаты одействиях редуктивных групп на алгебраич. многообразиях над полями характеристики 0 распространяются и на случай полей характеристики р>0. , служит алгебраич. стек, изучение свойств к-рого позволяет получить нек-рую информацию о пространстве модулей. Один из подходов к глобальной М. т. над
, служит алгебраич. стек, изучение свойств к-рого позволяет получить нек-рую информацию о пространстве модулей. Один из подходов к глобальной М. т. над  - это теория отображения периодов. Основным объектом здесь является классифицирующее пространство Dполяризованных Ходжа структур веса кдля заданных чисел Ходжа. Для семейства
- это теория отображения периодов. Основным объектом здесь является классифицирующее пространство Dполяризованных Ходжа структур веса кдля заданных чисел Ходжа. Для семейства  поляризованных алгебраич. многообразий над
поляризованных алгебраич. многообразий над  периоды определяют отображение Sв соответствующее классифицирующее пространство Dструктур Ходжа. Проблема модулей сводится к изучению условий биективности отображений периодов. Наличие локальной (глобальной) инъ-ективности для отображения периодов - это т. н. локальная (глобальная) проблема Торелли. На этом пути существование грубых пространств модулей доказано для кривых, абелевых многообразий и КЗ-поверхностей.
периоды определяют отображение Sв соответствующее классифицирующее пространство Dструктур Ходжа. Проблема модулей сводится к изучению условий биективности отображений периодов. Наличие локальной (глобальной) инъ-ективности для отображения периодов - это т. н. локальная (глобальная) проблема Торелли. На этом пути существование грубых пространств модулей доказано для кривых, абелевых многообразий и КЗ-поверхностей. ) многообразия
) многообразия  , содержащего Мв качестве плотного открытого подмножества, а также в описании и геометрич. интерпретации границы
, содержащего Мв качестве плотного открытого подмножества, а также в описании и геометрич. интерпретации границы  . В примере 1) естественной компактификацией грубого многообразия модулей
. В примере 1) естественной компактификацией грубого многообразия модулей  кривых рода
кривых рода  служит проективное многообразие модулей
служит проективное многообразие модулей  стабильных кривых. В примере 4) многообразие стабильных векторных расслоений ранга пи степени dна алгсбраич. кривой само является проективным и гладким, если (d, я)=1. Для поляризованных абелевых многообразий над
стабильных кривых. В примере 4) многообразие стабильных векторных расслоений ранга пи степени dна алгсбраич. кривой само является проективным и гладким, если (d, я)=1. Для поляризованных абелевых многообразий над  известны несколько способов компактификации многообразий модулей.
известны несколько способов компактификации многообразий модулей.