"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МОДЕЛЕЙ ТЕОРИЯ
Значение МОДЕЛЕЙ ТЕОРИЯ в математической энциклопедии:
- раздел математической логики, изучающий математические модели.
Начало М. т. относится к 30-м гг. 20 в., когда были доказаны следующие две основные теоремы.
Теорема 1 (теорема Гёделя - Мальцева). Если каждая конечная подсовокупность совокупности Твысказываний языка 1-й ступени совместима, то совместна и вся совокупность Т(см. [1]).
Теорема 2 (теорема Лёвенхейма - Сколема - Мальцева). Если совокупность высказываний языка 1-й ступени сигнатуры Wимеет бесконечную модель, то она имеет модель любой бесконечной мощности, не меньшей мощности сигнатуры W.
Теорема 1, называемая теоремой компактности, получила широкое применение в алгебре. На основе этой теоремы А. И. Мальцев создал метод доказательства локальных теорем алгебры (см. Мальцева локальные теоремы).
Пусть А- алгебраич. система сигнатуры  - основное множество системы
- основное множество системы  обозначает сигнатуру, получаемую из
обозначает сигнатуру, получаемую из  добавлением символов выделенных элементов
добавлением символов выделенных элементов  для всех
для всех  , а
, а  обозначает алгебраич. систему сигнатуры
обозначает алгебраич. систему сигнатуры  , к-рая является обогащением алгебраич. системы Aи в к-рой для каждого
, к-рая является обогащением алгебраич. системы Aи в к-рой для каждого  символ
символ  интерпретируется элементом а. Множество
интерпретируется элементом а. Множество  всех замкнутых формул сигнатуры
всех замкнутых формул сигнатуры  языка 1-й ступени, истинных в системе
языка 1-й ступени, истинных в системе  , наз. описанием алгебраической системы А, а множество D(А)тех формул из О(А), к-рые являются либ. <о атомными, либо отрицаниями атомных, наз. диаграммой А. Алгебраич. система Вназ. элементарным расширением алгебраич. системы А, если
, наз. описанием алгебраической системы А, а множество D(А)тех формул из О(А), к-рые являются либ. <о атомными, либо отрицаниями атомных, наз. диаграммой А. Алгебраич. система Вназ. элементарным расширением алгебраич. системы А, если  и
и  есть модель для
есть модель для  . В этом случае Аназ. элементарной подсистемой В. Напр., множество рациональных чисел вместе с обычным отношением порядка является элементарной подсистемой системы действительных чисел с обычным отношением порядка.
. В этом случае Аназ. элементарной подсистемой В. Напр., множество рациональных чисел вместе с обычным отношением порядка является элементарной подсистемой системы действительных чисел с обычным отношением порядка.
Подсистема Аалгебраич. системы Всигнатуры  тогда и только тогда является элементарной подсистемой системы В, когда для каждой замкнутой формулы
тогда и только тогда является элементарной подсистемой системы В, когда для каждой замкнутой формулы  языка 1-й ступени сигнатуры
языка 1-й ступени сигнатуры  , истинной в
, истинной в  , найдется такой
, найдется такой  , что
, что  истинна в
истинна в  . Из этого критерия сразу следует, что объединение возрастающей цепочки элементарных подсистем является элементарным расширением каждой из этих систем. Если замкнутая
. Из этого критерия сразу следует, что объединение возрастающей цепочки элементарных подсистем является элементарным расширением каждой из этих систем. Если замкнутая  -формула языка 1-й ступени истинна в каждой системе возрастающей цепочки систем, то эта формула истинна и в объединении этой цепочки (см. [1]).
-формула языка 1-й ступени истинна в каждой системе возрастающей цепочки систем, то эта формула истинна и в объединении этой цепочки (см. [1]).
Пусть сигнатура  содержит символ Uодноместного отношения. Говорят, что модель Атеории Тсигнатуры
содержит символ Uодноместного отношения. Говорят, что модель Атеории Тсигнатуры  имеет тип
имеет тип  , если мощность Аравна
, если мощность Аравна  , а мощность
, а мощность  равна
равна 
Теорема Вота: если элементарная теория Тсчетной сигнатуры имеет модель типа  , где
, где  , то Тимеет модель типа
, то Тимеет модель типа  (см. [7], [10]). В предположении, что справедлива обобщенная гипотеза континуума, элементарная теория счетной сигнатуры имеет модель типа
(см. [7], [10]). В предположении, что справедлива обобщенная гипотеза континуума, элементарная теория счетной сигнатуры имеет модель типа  для каждого
для каждого  , если она имеет модель типа
, если она имеет модель типа  (см. [10]). При этом же предположении теория Тh(А), где сигнатура Аесть
(см. [10]). При этом же предположении теория Тh(А), где сигнатура Аесть  - множество всех действительных чисел,
- множество всех действительных чисел,  - множество целых чисел, а
- множество целых чисел, а  определены обычным образом, не имеет модели типа
определены обычным образом, не имеет модели типа 
Пусть  обозначает обогащение алгебраич. системы Апри помощи предиката
обозначает обогащение алгебраич. системы Апри помощи предиката  , а
, а  - сигнатуру, полученную из
- сигнатуру, полученную из  присоединением предикатного символа Р. Во многих случаях важно понять, когда в каждой системе из класса Калгебраич. систем сигнатуры
присоединением предикатного символа Р. Во многих случаях важно понять, когда в каждой системе из класса Калгебраич. систем сигнатуры  предикат Рзадается формулой языка 1-й ступени сигнатуры
предикат Рзадается формулой языка 1-й ступени сигнатуры  . Частичный ответ на этот вопрос дает теорема Бета: тогда и только тогда существует формула
. Частичный ответ на этот вопрос дает теорема Бета: тогда и только тогда существует формула  языка 1-й ступени сигнатуры
языка 1-й ступени сигнатуры  такая, что формула
такая, что формула  истинна на всех системах аксиоматизируемого класса Ксигнатуры
истинна на всех системах аксиоматизируемого класса Ксигнатуры  , когда множество
, когда множество  содержит не более одного элемента для каждой алгебраич. системы Асигнатуры
содержит не более одного элемента для каждой алгебраич. системы Асигнатуры  (см. [2]).
(см. [2]).
Многие исследования по М. т. связаны с изучением свойств, сохраняющихся при операциях над алгебраич. системами. К числу важнейших операций относятся гомоморфизмы, прямые и фильтрованные произведения.
Говорят, что высказывание Ф устойчиво относительно гомоморфизмов, если из истинности Ф в алгебраич. системе Аследует истинность Ф во всех эпиморфных образах А. Формула Ф языка 1-й ступени наз. положительно й, если Ф не содержит знаков отрицания и импликации. Доказано (см. [1]), что высказывание Ф языка 1-й ступени устойчиво относительно гомоморфизмов тогда и только тогда, когда Ф эквивалентно положительному высказыванию. Аналогичная теорема верна и для языка 
Формула  языка 1-й ступени сигнатуры
языка 1-й ступени сигнатуры  наз. хорновской, если она может быть получена конъюнкциями и навешиванием кванторов из формул вида
наз. хорновской, если она может быть получена конъюнкциями и навешиванием кванторов из формул вида  где
где  - атомные формулы языка 1-й ступени сигнатуры
- атомные формулы языка 1-й ступени сигнатуры  . Примерами хорновских формул являются тождества и квазнтождества. Центральной в теории ультрапронзведений является теорема Лося
. Примерами хорновских формул являются тождества и квазнтождества. Центральной в теории ультрапронзведений является теорема Лося  : всякая формула языка 1-й ступени фильтруется по любому ультрафильтру (см. [1]). Формула языка 1-й ступени условно фильтруется по любому фильтру тогда и только тогда, когда эта формула эквивалентна хорновской формуле. Имеет место теорема (см. [9]): алгебраич. системы Аи Всигнатуры
: всякая формула языка 1-й ступени фильтруется по любому ультрафильтру (см. [1]). Формула языка 1-й ступени условно фильтруется по любому фильтру тогда и только тогда, когда эта формула эквивалентна хорновской формуле. Имеет место теорема (см. [9]): алгебраич. системы Аи Всигнатуры  тогда и только тогда элементарно эквивалентны, когда существует такой ультрафильтр Dна множестве
тогда и только тогда элементарно эквивалентны, когда существует такой ультрафильтр Dна множестве  , что
, что  и
и  изоморфны. Мощность фильтрованного произведения бесконечна, если для каждого натурального пчисло сомножителей мощности пконечно. Если для каждого натурального пмножество тех индексов, для к-рых соответствующий сомножитель имеет мощность п, не принадлежит D, то мощность ультрапроизведения по неглавному ультрафильтру Uна счетном множестве I равна континууму. Для каждого бесконечного I мощности
изоморфны. Мощность фильтрованного произведения бесконечна, если для каждого натурального пчисло сомножителей мощности пконечно. Если для каждого натурального пмножество тех индексов, для к-рых соответствующий сомножитель имеет мощность п, не принадлежит D, то мощность ультрапроизведения по неглавному ультрафильтру Uна счетном множестве I равна континууму. Для каждого бесконечного I мощности  существует такой фильтр Dна I, что для каждого фильтра
существует такой фильтр Dна I, что для каждого фильтра  на I, содержащего D, и каждого бесконечного множества Амощность
на I, содержащего D, и каждого бесконечного множества Амощность  не меньше
не меньше  (см. [1]).
(см. [1]).
Много применений находит теорема о существовании моделей с большим числом автоморфизмов (см. [3]): для любого линейно упорядоченного множества Xв аксиоматизируемом классе Калгебраич. систем, содержащем бесконечную систему, существует такая система А, что  и каждое сохраняющее порядок одно-однозначное отображение Xна Xпродолжается до автоморфизма А.
и каждое сохраняющее порядок одно-однозначное отображение Xна Xпродолжается до автоморфизма А.
Важными понятиями М. т. являются понятия универсальной, однородной и насыщенной систем. Пусть Аи В - алгебраич. системы сигнатуры  . Отображение f множества
. Отображение f множества  во множество
во множество  наз. элементарным, если для каждой формулы
наз. элементарным, если для каждой формулы  языка 1-й ступени сигнатуры
языка 1-й ступени сигнатуры  и любых
и любых  имеет место эквивалентность
имеет место эквивалентность 
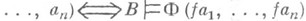 . Система Аназ.
. Система Аназ. -универсальной, если для каждой системы В, элементарно эквивалентной системе Аи имеющей мощность, не превосходящую
-универсальной, если для каждой системы В, элементарно эквивалентной системе Аи имеющей мощность, не превосходящую  , существует элементарное отображение
, существует элементарное отображение  в
в  . Система Аназ.
. Система Аназ. -однородной, если для любого множества
-однородной, если для любого множества  , мощность к-рого меньше
, мощность к-рого меньше  , каждое элементарное отображение
, каждое элементарное отображение  в
в  продолжается до элементарного отображения
продолжается до элементарного отображения  на
на  (т. е. до автоморфизма А). Система Асигнатуры
(т. е. до автоморфизма А). Система Асигнатуры  наз.
наз. -насыщенной, если для каждого множества
-насыщенной, если для каждого множества  , мощность к-рого меньше
, мощность к-рого меньше  , и каждой совокупности
, и каждой совокупности  формул языка 1-й ступени сигнатуры
формул языка 1-й ступени сигнатуры  , не содержащих свободных переменных, отличных от
, не содержащих свободных переменных, отличных от  , из конечной выполнимости
, из конечной выполнимости  в
в  следует выполнимость
следует выполнимость  в
в  . Система Аназ. универсальной (соответственно однородной или насыщенной), если и Аявляется
. Система Аназ. универсальной (соответственно однородной или насыщенной), если и Аявляется  универсальной (соответственно
универсальной (соответственно  -однородной или
-однородной или  насыщенной), где
насыщенной), где  есть мощность
есть мощность  . Система тогда и только тогда насыщена, когда она одновременно универсальна и однородна. Две элементарно эквивалентные насыщенные системы одной мощности изоморфны (см. [3]). Все несчетные модели категоричной в несчетных мощностях элементарной теории счетной сигнатуры насыщены (теорема Морли, см. [3], [8]). Большое число примеров
. Система тогда и только тогда насыщена, когда она одновременно универсальна и однородна. Две элементарно эквивалентные насыщенные системы одной мощности изоморфны (см. [3]). Все несчетные модели категоричной в несчетных мощностях элементарной теории счетной сигнатуры насыщены (теорема Морли, см. [3], [8]). Большое число примеров  -насыщенных систем доставляют ультрапроизведения. Напр., если D- неглавный ультрафильтр на счетном множестве
-насыщенных систем доставляют ультрапроизведения. Напр., если D- неглавный ультрафильтр на счетном множестве  , то
, то  является
является  -насыщенной системой для любых алгебраич. систем
-насыщенной системой для любых алгебраич. систем  счетной сигнатуры
счетной сигнатуры  .
.
Основными задачами М. т. являются изучение выразительной возможности формализованного языка и изучение классов структур, определимых средствами этого языка. Найдены нек-рые важные свойства стабильных теорий, еще более детально изучены классы категоричных и суперстабильных теорий.
Основным аппаратом при изучении стабильных теорий является классификация формул и локально совместных множеств формул в этих теориях.
Такая классификация осуществляется путем приписывания формулам рангов. Эти ранги обычно принимают в качестве значений ординалы, а рангующие функции задаются с помощью специальных топологий или другим способом. Изучение рангующих функций и их усовершенствование - богатый источник информации о теориях.
В изучении классов моделей выясняют число различных с точностью до изоморфизма моделей теории в рассматриваемой мощности и наличие специальных моделей, напр, простых, минимальных, насыщенных, однородных, универсальных, конструктивизируемых и т. п., и создают способы их построения.
Классич. примерами применения методов М. т. в математич. анализе являются работы А. Робинсона (A. Robinson) и его школы, сформировавшиеся в самостоятельную науку - нестандартный анализ;благодаря работам А. И. Мальцева и его школы развивается применение методов М. т. в топологич. алгебре; новейшие результаты о свойствах стабильных теорий находят использование при изучении конкретных алгебраич. вопросов.
Перечисленные выше проблемы встают и при изучении различных неэлементарных языков, напр., получаемых добавлением новых кванторов, введением в рассмотрение бесконечных выражений, модальностей и т. п.
Лит.:[1] Мальцев А. И., Алгебраические системы, М., 1970; [2] Робинсон А., Введение в теорию моделей и метаматематику алгебры, пер. с англ., М., 1967; [3] Тайцлин М. А., Теория моделей, Новосиб., 1970; [4] Ершов Ю. Л., Проблемы разрешимости и конструктивные модели, М., 1980; [5] Ершов Ю. Л., Палютин Е. А., Математическая логика, М., 1979; [6] Ершов Ю. Л. [и др.]. "Успехи матем. наук", 1965, т. 20, в. 4, с. 37 -108; [7] Мальцев А. И.,Тр. Четвертого Всесоюзного математического съезда, т. 1, Л., 1963, с. 169-98; [8] Кейслер Г., Чэн Ч. Ч., Теория моделей, пер. с англ., М., 1977; [9] Сакс Д ж.,, Теория насыщенных моделей, пер. с англ., М., 1976; [10] Vaught R.L., в сб.: Infinistic methods, N. Y. [а. о.], 1961, р. 303-21; [11] Моrlеу М., Vaught R.,"Math. scand.", 1962, v. 11, fasc. 1, p. 37-57; [12] Mоrleу М., "Trans. Amer. Math. Soc", 1965, v. 114, № 2, p. 514-38; [13] Shclah S., Classification theory and the number of non-isomorphic models, Amst., 1978; [14] Bell I. L., Slоmsоn А. В., Models and ultraproduets. An introduction, Amst.- L., 1969.
А. Д. Тайманов, M. А. Тайцлин.

 - основное множество системы
- основное множество системы  обозначает сигнатуру, получаемую из
обозначает сигнатуру, получаемую из  добавлением символов выделенных элементов
добавлением символов выделенных элементов  для всех
для всех  , а
, а  обозначает алгебраич. систему сигнатуры
обозначает алгебраич. систему сигнатуры  , к-рая является обогащением алгебраич. системы Aи в к-рой для каждого
, к-рая является обогащением алгебраич. системы Aи в к-рой для каждого  символ
символ  интерпретируется элементом а. Множество
интерпретируется элементом а. Множество  всех замкнутых формул сигнатуры
всех замкнутых формул сигнатуры  языка 1-й ступени, истинных в системе
языка 1-й ступени, истинных в системе  , наз. описанием алгебраической системы А, а множество D(А)тех формул из О(А), к-рые являются либ. <о атомными, либо отрицаниями атомных, наз. диаграммой А. Алгебраич. система Вназ. элементарным расширением алгебраич. системы А, если
, наз. описанием алгебраической системы А, а множество D(А)тех формул из О(А), к-рые являются либ. <о атомными, либо отрицаниями атомных, наз. диаграммой А. Алгебраич. система Вназ. элементарным расширением алгебраич. системы А, если  и
и  есть модель для
есть модель для  . В этом случае Аназ. элементарной подсистемой В. Напр., множество рациональных чисел вместе с обычным отношением порядка является элементарной подсистемой системы действительных чисел с обычным отношением порядка.
. В этом случае Аназ. элементарной подсистемой В. Напр., множество рациональных чисел вместе с обычным отношением порядка является элементарной подсистемой системы действительных чисел с обычным отношением порядка. тогда и только тогда является элементарной подсистемой системы В, когда для каждой замкнутой формулы
тогда и только тогда является элементарной подсистемой системы В, когда для каждой замкнутой формулы  языка 1-й ступени сигнатуры
языка 1-й ступени сигнатуры  , истинной в
, истинной в  , найдется такой
, найдется такой  , что
, что  истинна в
истинна в  . Из этого критерия сразу следует, что объединение возрастающей цепочки элементарных подсистем является элементарным расширением каждой из этих систем. Если замкнутая
. Из этого критерия сразу следует, что объединение возрастающей цепочки элементарных подсистем является элементарным расширением каждой из этих систем. Если замкнутая  -формула языка 1-й ступени истинна в каждой системе возрастающей цепочки систем, то эта формула истинна и в объединении этой цепочки (см. [1]).
-формула языка 1-й ступени истинна в каждой системе возрастающей цепочки систем, то эта формула истинна и в объединении этой цепочки (см. [1]). содержит символ Uодноместного отношения. Говорят, что модель Атеории Тсигнатуры
содержит символ Uодноместного отношения. Говорят, что модель Атеории Тсигнатуры  имеет тип
имеет тип  , если мощность Аравна
, если мощность Аравна  , а мощность
, а мощность  равна
равна 
 , где
, где  , то Тимеет модель типа
, то Тимеет модель типа  (см. [7], [10]). В предположении, что справедлива обобщенная гипотеза континуума, элементарная теория счетной сигнатуры имеет модель типа
(см. [7], [10]). В предположении, что справедлива обобщенная гипотеза континуума, элементарная теория счетной сигнатуры имеет модель типа  для каждого
для каждого  , если она имеет модель типа
, если она имеет модель типа  (см. [10]). При этом же предположении теория Тh(А), где сигнатура Аесть
(см. [10]). При этом же предположении теория Тh(А), где сигнатура Аесть  - множество всех действительных чисел,
- множество всех действительных чисел,  - множество целых чисел, а
- множество целых чисел, а  определены обычным образом, не имеет модели типа
определены обычным образом, не имеет модели типа 
 обозначает обогащение алгебраич. системы Апри помощи предиката
обозначает обогащение алгебраич. системы Апри помощи предиката  , а
, а  - сигнатуру, полученную из
- сигнатуру, полученную из  присоединением предикатного символа Р. Во многих случаях важно понять, когда в каждой системе из класса Калгебраич. систем сигнатуры
присоединением предикатного символа Р. Во многих случаях важно понять, когда в каждой системе из класса Калгебраич. систем сигнатуры  предикат Рзадается формулой языка 1-й ступени сигнатуры
предикат Рзадается формулой языка 1-й ступени сигнатуры  . Частичный ответ на этот вопрос дает теорема Бета: тогда и только тогда существует формула
. Частичный ответ на этот вопрос дает теорема Бета: тогда и только тогда существует формула  языка 1-й ступени сигнатуры
языка 1-й ступени сигнатуры  такая, что формула
такая, что формула  истинна на всех системах аксиоматизируемого класса Ксигнатуры
истинна на всех системах аксиоматизируемого класса Ксигнатуры  , когда множество
, когда множество  содержит не более одного элемента для каждой алгебраич. системы Асигнатуры
содержит не более одного элемента для каждой алгебраич. системы Асигнатуры  (см. [2]).
(см. [2]).
 языка 1-й ступени сигнатуры
языка 1-й ступени сигнатуры  наз. хорновской, если она может быть получена конъюнкциями и навешиванием кванторов из формул вида
наз. хорновской, если она может быть получена конъюнкциями и навешиванием кванторов из формул вида  где
где  - атомные формулы языка 1-й ступени сигнатуры
- атомные формулы языка 1-й ступени сигнатуры  . Примерами хорновских формул являются тождества и квазнтождества. Центральной в теории ультрапронзведений является теорема Лося
. Примерами хорновских формул являются тождества и квазнтождества. Центральной в теории ультрапронзведений является теорема Лося  : всякая формула языка 1-й ступени фильтруется по любому ультрафильтру (см. [1]). Формула языка 1-й ступени условно фильтруется по любому фильтру тогда и только тогда, когда эта формула эквивалентна хорновской формуле. Имеет место теорема (см. [9]): алгебраич. системы Аи Всигнатуры
: всякая формула языка 1-й ступени фильтруется по любому ультрафильтру (см. [1]). Формула языка 1-й ступени условно фильтруется по любому фильтру тогда и только тогда, когда эта формула эквивалентна хорновской формуле. Имеет место теорема (см. [9]): алгебраич. системы Аи Всигнатуры  тогда и только тогда элементарно эквивалентны, когда существует такой ультрафильтр Dна множестве
тогда и только тогда элементарно эквивалентны, когда существует такой ультрафильтр Dна множестве  , что
, что  и
и  изоморфны. Мощность фильтрованного произведения бесконечна, если для каждого натурального пчисло сомножителей мощности пконечно. Если для каждого натурального пмножество тех индексов, для к-рых соответствующий сомножитель имеет мощность п, не принадлежит D, то мощность ультрапроизведения по неглавному ультрафильтру Uна счетном множестве I равна континууму. Для каждого бесконечного I мощности
изоморфны. Мощность фильтрованного произведения бесконечна, если для каждого натурального пчисло сомножителей мощности пконечно. Если для каждого натурального пмножество тех индексов, для к-рых соответствующий сомножитель имеет мощность п, не принадлежит D, то мощность ультрапроизведения по неглавному ультрафильтру Uна счетном множестве I равна континууму. Для каждого бесконечного I мощности  существует такой фильтр Dна I, что для каждого фильтра
существует такой фильтр Dна I, что для каждого фильтра  на I, содержащего D, и каждого бесконечного множества Амощность
на I, содержащего D, и каждого бесконечного множества Амощность  не меньше
не меньше  (см. [1]).
(см. [1]). и каждое сохраняющее порядок одно-однозначное отображение Xна Xпродолжается до автоморфизма А.
и каждое сохраняющее порядок одно-однозначное отображение Xна Xпродолжается до автоморфизма А. . Отображение f множества
. Отображение f множества  во множество
во множество  наз. элементарным, если для каждой формулы
наз. элементарным, если для каждой формулы  языка 1-й ступени сигнатуры
языка 1-й ступени сигнатуры  и любых
и любых  имеет место эквивалентность
имеет место эквивалентность 
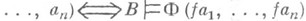 . Система Аназ.
. Система Аназ. -универсальной, если для каждой системы В, элементарно эквивалентной системе Аи имеющей мощность, не превосходящую
-универсальной, если для каждой системы В, элементарно эквивалентной системе Аи имеющей мощность, не превосходящую  , существует элементарное отображение
, существует элементарное отображение  в
в  . Система Аназ.
. Система Аназ. -однородной, если для любого множества
-однородной, если для любого множества  , мощность к-рого меньше
, мощность к-рого меньше  , каждое элементарное отображение
, каждое элементарное отображение  в
в  продолжается до элементарного отображения
продолжается до элементарного отображения  на
на  (т. е. до автоморфизма А). Система Асигнатуры
(т. е. до автоморфизма А). Система Асигнатуры  наз.
наз. -насыщенной, если для каждого множества
-насыщенной, если для каждого множества  , мощность к-рого меньше
, мощность к-рого меньше  , и каждой совокупности
, и каждой совокупности  формул языка 1-й ступени сигнатуры
формул языка 1-й ступени сигнатуры  , не содержащих свободных переменных, отличных от
, не содержащих свободных переменных, отличных от  , из конечной выполнимости
, из конечной выполнимости  в
в  следует выполнимость
следует выполнимость  в
в  . Система Аназ. универсальной (соответственно однородной или насыщенной), если и Аявляется
. Система Аназ. универсальной (соответственно однородной или насыщенной), если и Аявляется  универсальной (соответственно
универсальной (соответственно  -однородной или
-однородной или  насыщенной), где
насыщенной), где  есть мощность
есть мощность  . Система тогда и только тогда насыщена, когда она одновременно универсальна и однородна. Две элементарно эквивалентные насыщенные системы одной мощности изоморфны (см. [3]). Все несчетные модели категоричной в несчетных мощностях элементарной теории счетной сигнатуры насыщены (теорема Морли, см. [3], [8]). Большое число примеров
. Система тогда и только тогда насыщена, когда она одновременно универсальна и однородна. Две элементарно эквивалентные насыщенные системы одной мощности изоморфны (см. [3]). Все несчетные модели категоричной в несчетных мощностях элементарной теории счетной сигнатуры насыщены (теорема Морли, см. [3], [8]). Большое число примеров  -насыщенных систем доставляют ультрапроизведения. Напр., если D- неглавный ультрафильтр на счетном множестве
-насыщенных систем доставляют ультрапроизведения. Напр., если D- неглавный ультрафильтр на счетном множестве  , то
, то  является
является  -насыщенной системой для любых алгебраич. систем
-насыщенной системой для любых алгебраич. систем  счетной сигнатуры
счетной сигнатуры  .
.