"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МНОЖЕСТВЕННЫЙ КОЭФФИЦИЕНТ КОРРЕЛЯЦИИЗначение МНОЖЕСТВЕННЫЙ КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ в математической энциклопедии:
- мера линейной зависимости между одной и нек-рой совокупностью случайных величин. Точнее, если  случайный вектор со значениями в случайный вектор со значениями в  , то М. к. к. между , то М. к. к. между  определяется как обычный коэффициент корреляции между Х 1 и наилучшим линейным приближением определяется как обычный коэффициент корреляции между Х 1 и наилучшим линейным приближением  по по   т. е. регрессией т. е. регрессией  величины величины  по по  . М. к. к. обладает тем свойством, что если при . М. к. к. обладает тем свойством, что если при   есть регрессия есть регрессия  по по  то среди всех линейных комбинаций величин то среди всех линейных комбинаций величин  величина величина  имеет наибольшую корреляцию с имеет наибольшую корреляцию с  ; в этом смысле М. к. к.- частный случай канонич. коэффициента корреляции. При к -2 М. к. к. равен обычному коэффициенту корреляции ; в этом смысле М. к. к.- частный случай канонич. коэффициента корреляции. При к -2 М. к. к. равен обычному коэффициенту корреляции  между между  . М. к. к. между . М. к. к. между  обозначается обозначается  и выражается через элементы корреляционной матрицы и выражается через элементы корреляционной матрицы 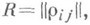  следующим образом следующим образом 
где  - определитель - определитель  алгебраич. дополнение элемента алгебраич. дополнение элемента  ; при этом ; при этом  . Если . Если  , то величина Х 1 с вероятностью 1 равна нек-рой линейной комбинации величин , то величина Х 1 с вероятностью 1 равна нек-рой линейной комбинации величин  т. е. совместное распределение величин т. е. совместное распределение величин  сосредоточено в нек-рой гиперплоскости пространства сосредоточено в нек-рой гиперплоскости пространства  . С другой стороны, . С другой стороны, тогда и только тогда, когда тогда и только тогда, когда  т. е. когда т. е. когда  не коррелирована ни с одной из величин не коррелирована ни с одной из величин  Для вычисления М. к. к. можно также использовать формулу Для вычисления М. к. к. можно также использовать формулу  где где  - дисперсия - дисперсия  , а , а  - дисперсия X1 относительно регрессии. - дисперсия X1 относительно регрессии. Выборочным аналогом М. к. к.  является является 
где  и и  - оценки - оценки  и и  по выборке объема п. Для проверки гипотезы об отсутствии связи используются выборочные распределения по выборке объема п. Для проверки гипотезы об отсутствии связи используются выборочные распределения  . При условии, что выборка произведена из многомерной нормальной совокупности, величина . При условии, что выборка произведена из многомерной нормальной совокупности, величина  имеет бета-распределение с параметрами имеет бета-распределение с параметрами  , если , если  ; если ; если  , то величина , то величина  при при  имеет в пределе нецентральное "хи-квадрат"-распределение с к-1 степенями свободы и параметром нецентральности имеет в пределе нецентральное "хи-квадрат"-распределение с к-1 степенями свободы и параметром нецентральности  Лит.:[1] Крамер Г., Математические методы статистики, пер. с англ., 2 изд., М., 1975; [2] Кендалл М., Стьюарт А., Статистические выводы и связи, пер. с англ., М., 1973. А. В. Прохоров.
|

 случайный вектор со значениями в
случайный вектор со значениями в  , то М. к. к. между
, то М. к. к. между  определяется как обычный коэффициент корреляции между Х 1 и наилучшим линейным приближением
определяется как обычный коэффициент корреляции между Х 1 и наилучшим линейным приближением  по
по 
 т. е. регрессией
т. е. регрессией  величины
величины  по
по  . М. к. к. обладает тем свойством, что если при
. М. к. к. обладает тем свойством, что если при 
 есть регрессия
есть регрессия  по
по  то среди всех линейных комбинаций величин
то среди всех линейных комбинаций величин  величина
величина  имеет наибольшую корреляцию с
имеет наибольшую корреляцию с  ; в этом смысле М. к. к.- частный случай канонич. коэффициента корреляции. При к -2 М. к. к. равен обычному коэффициенту корреляции
; в этом смысле М. к. к.- частный случай канонич. коэффициента корреляции. При к -2 М. к. к. равен обычному коэффициенту корреляции  между
между  . М. к. к. между
. М. к. к. между  обозначается
обозначается  и выражается через элементы корреляционной матрицы
и выражается через элементы корреляционной матрицы 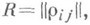
 следующим образом
следующим образом
 - определитель
- определитель  алгебраич. дополнение элемента
алгебраич. дополнение элемента  ; при этом
; при этом  . Если
. Если  , то величина Х 1 с вероятностью 1 равна нек-рой линейной комбинации величин
, то величина Х 1 с вероятностью 1 равна нек-рой линейной комбинации величин  т. е. совместное распределение величин
т. е. совместное распределение величин  сосредоточено в нек-рой гиперплоскости пространства
сосредоточено в нек-рой гиперплоскости пространства  . С другой стороны,
. С другой стороны, тогда и только тогда, когда
тогда и только тогда, когда  т. е. когда
т. е. когда  не коррелирована ни с одной из величин
не коррелирована ни с одной из величин  Для вычисления М. к. к. можно также использовать формулу
Для вычисления М. к. к. можно также использовать формулу  где
где  - дисперсия
- дисперсия  , а
, а  - дисперсия X1 относительно регрессии.
- дисперсия X1 относительно регрессии. является
является
 и
и  - оценки
- оценки  и
и  по выборке объема п. Для проверки гипотезы об отсутствии связи используются выборочные распределения
по выборке объема п. Для проверки гипотезы об отсутствии связи используются выборочные распределения  . При условии, что выборка произведена из многомерной нормальной совокупности, величина
. При условии, что выборка произведена из многомерной нормальной совокупности, величина  имеет бета-распределение с параметрами
имеет бета-распределение с параметрами  , если
, если  ; если
; если  , то величина
, то величина  при
при  имеет в пределе нецентральное "хи-квадрат"-распределение с к-1 степенями свободы и параметром нецентральности
имеет в пределе нецентральное "хи-квадрат"-распределение с к-1 степенями свободы и параметром нецентральности 