|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МНОГОЧЛЕНЗначение МНОГОЧЛЕН в математической энциклопедии: полином,- выражение вида
где
наз. членами М. Порядок членов, а также порядок множителей в каждом члене можно менять произвольно; тёчно так же можно вводить или опускать члены с нулевыми коэффициентами, а в каждом отдельном члене - степени с нулевыми показателями. В случае, когда М. имеет один, два или три члена, его наз. одночленом, двучленом или трехчленом. Относительно коэффициентов М. предполагается, что они принадлежат нек-рому полю, напр, полю рациональных, действительных или комплексных чисел. Два члена М. наз. подобными, если в них показатели степеней при одинаковых переменных попарно равны. Подобные между собой члены
можно заменить одним
(приведение подобных членов). Два М. наз. равными, если после приведения подобных все члены с отличными от нуля коэффициентами оказываются попарно одинаковыми (но, может быть, записанными в разном порядке), а также если все коэффициенты этих М. оказываются равными нулю. В последнем случае М. наз. тождественным нулем и обозначают знаком 0. Сумму показателей степеней какого-либо члена М. наз. степенью этого члена. Если М. не тождественный нуль, то среди членов с отличными от нуля коэффициентами (предполагается, что все подобные члены приведены) имеются один или несколько наибольшей степени; эту наибольшую степень наз. степенью М. Тождественный нуль не имеет степени. М. нулевой степени сводится к одному члену А(постоянному, не равному нулю). М. от переменных х 1, х2, . . ., х п наз. симметрическим многочленом, если он не меняется ни при какой перестановке неизвестных. М., все члены к-рого одинаковой степени, наз. однородным многочленом, или формой; формы первой, второй и третьей степеней наз. линейными, квадратичными, кубическими, а по числу переменных (два, три)-двоичными (бинарными), тройничными (тернарными) (напр., Степенью многочлена
где Корнем многочлена от одного неизвестного над полем кназ. решение алгебраического уравнения Корни М. связаны с его коэффициентами формулами Впета (см. Виета теорема). Совокупность всевозможных различных М. от ппеременных с коэффициентами из данного поля образует кольцо относительно естественным образом определяемых операций сложения и умножения. Рассматриваются также кольца М. от бесконечного множества переменных. Многочленов кольца являются ассоциативно-коммутативными кольцами без делителей нуля (т. е. произведение М., не равных 0, не может дать 0). Если для двух многочленов Ри Qможно найти такой многочлен В, что Посредством повторного применения этой операции можно находить наибольший общий делитель Ри Q, т. е. такой делитель Ри Q, к-рый делится на любой общий делитель этих М. (см. Евклида алгоритм). Два М., наибольший общий делитель к-рых равен 1, наз. взаимно простыми. М., к-рый можно представить в виде произведения М. низших степеней с коэффициентами из данного поля, наз. приводимым (в данном поле), в противном случае - неприводимым. Неприводимые М. играют в кольце М. роль, сходную с ролью простых чисел в кольце целых чисел. Напр., верна теорема: если произведение PQ делится на неприводимый многочлен В, а Р на Вне делится, то Qдолжен делиться на В. Каждый М., степени большей нуля, разлагается в данном поле в произведение неприводимых множителей единственным образом (с точностью до множителей нулейой степени). Напр., многочлен Если переменным К числу важнейших свойств М. относится то, что любую непрерывную функцию можно с произвольно малой ошибкой, заменить М. (см. Вейерштрасса теорема). Специальные системы М.- ортогональные многочлены- используются в теории приближения как средство представления функций в виде рядов. В элементарной алгебре М. иногда наз. такие ал-гебраич. выражения, в к-рых последним действием является сложение или вычитание. Лит.:[1] Мишина А. П., Проскуряков И. В., Высшая алгебра. Линейная алгебра, многочлены, общая алгебра, 2 изд., М., 1965; [2] Курош А. Г., Курс высшей алгебры, 11 изд., М., 1975; [3] Бурбаки Н., Алгебра. Многочлены и поля. Упорядоченные группы, пер. с франц., М., 1965. А. И. Маркушевич. |
|
|
|


 - переменные, а А, В, ..., D (коэффициент ы М.) и x, y, .. ., w (показатели степеней - целые неотрицательные числа) - постоянные. Отдельные слагаемые вида
- переменные, а А, В, ..., D (коэффициент ы М.) и x, y, .. ., w (показатели степеней - целые неотрицательные числа) - постоянные. Отдельные слагаемые вида



 есть тройничная квадратичная форма).
есть тройничная квадратичная форма). по отношению к одному из переменных
по отношению к одному из переменных  наз. наивысший показатель, с к-рым .xi входит в члены этого М. (эта степень может быть и нулевой). Из двух членов М. тот считается выше (Относительно данной нумерации переменных), у к-рого показатель при х 1. больше, а если эти показатели равны, то тот, у к-рого показатели при
наз. наивысший показатель, с к-рым .xi входит в члены этого М. (эта степень может быть и нулевой). Из двух членов М. тот считается выше (Относительно данной нумерации переменных), у к-рого показатель при х 1. больше, а если эти показатели равны, то тот, у к-рого показатели при 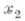 больше, и т. д. Если все члены М. расположены в таком порядке, что каждый следующий член ниже предыдущего, то говорят, что члены этого М. расположены лексикографически. Тот член, к-рый при этом стоит на первом месте, наз. высшим членом многочлена. М. от одного переменного, члены к-рого расположены в лексико-графич. порядке, имеет вид
больше, и т. д. Если все члены М. расположены в таком порядке, что каждый следующий член ниже предыдущего, то говорят, что члены этого М. расположены лексикографически. Тот член, к-рый при этом стоит на первом месте, наз. высшим членом многочлена. М. от одного переменного, члены к-рого расположены в лексико-графич. порядке, имеет вид
 - коэффициенты.
- коэффициенты.
 то говорят, что Рделится на Q; Q наз. делителем, а В- частным. Если Рне делится на Q, но оба М. содержат одно и то же переменное, напр, х, и степень Рпо отношению к хесть п, а степень Qесть
то говорят, что Рделится на Q; Q наз. делителем, а В- частным. Если Рне делится на Q, но оба М. содержат одно и то же переменное, напр, х, и степень Рпо отношению к хесть п, а степень Qесть  , то можно найти такие многочлены р, R и S, что pP=QR+S, причем рсовсем не содержит х, а в Sпеременное хсодержится в степени ниже т. В случае, когда хявляется единственным переменным, можно рсчитать равным 1; тогда операцию отыскания Ви Sпо Ри Qназ. делением с остатком; деление с остатком можно производить с помощью Горнера схемы.
, то можно найти такие многочлены р, R и S, что pP=QR+S, причем рсовсем не содержит х, а в Sпеременное хсодержится в степени ниже т. В случае, когда хявляется единственным переменным, можно рсчитать равным 1; тогда операцию отыскания Ви Sпо Ри Qназ. делением с остатком; деление с остатком можно производить с помощью Горнера схемы. , неприводимый в поле рациональных чисел, разлагается на два множителя в поле действительных чисел и на четыре множителя в поле комплексных чисел. Вообще, каждый М. от одного переменного хразлагается в поле действительных чисел на множители первой и второй степени, в поле комплексных чисел - на множители первой степени (алгебры основная теорема). Для двух и большего числа переменных этого уже нельзя утверждать. Над любым полем кдля любого
, неприводимый в поле рациональных чисел, разлагается на два множителя в поле действительных чисел и на четыре множителя в поле комплексных чисел. Вообще, каждый М. от одного переменного хразлагается в поле действительных чисел на множители первой и второй степени, в поле комплексных чисел - на множители первой степени (алгебры основная теорема). Для двух и большего числа переменных этого уже нельзя утверждать. Над любым полем кдля любого  существуют М. от ппеременных, неприводимые в любом расширении поля к. Такие М. наз. абсолютно неприводимыми. Напр., многочлен
существуют М. от ппеременных, неприводимые в любом расширении поля к. Такие М. наз. абсолютно неприводимыми. Напр., многочлен  неприводим в любом числовом поле.
неприводим в любом числовом поле.  придать определенные числовые значения (напр., действительные или комплексные), то М. также получит определенное числовое значение. Таким образом, каждый М. можно рассматривать как функцию соответствующих переменных. Эта функция непрерывна и дифференцируема при любых значениях переменных; ее можно характеризовать как целую рациональную функцию, т. е. функцию, получающуюся из переменных и нек-рых постоянных (коэффициентов) посредством выполнения в определенном порядке действий сложения, вычитания и умножения. Целые рациональные функции входят в более широкий класс рациональных функций, где к перечисленным действиям: присоединяется деление: любую рациональную функцию можно представить в виде частного двух М. Наконец, рациональные функции содержатся в классе алгебраических функций.
придать определенные числовые значения (напр., действительные или комплексные), то М. также получит определенное числовое значение. Таким образом, каждый М. можно рассматривать как функцию соответствующих переменных. Эта функция непрерывна и дифференцируема при любых значениях переменных; ее можно характеризовать как целую рациональную функцию, т. е. функцию, получающуюся из переменных и нек-рых постоянных (коэффициентов) посредством выполнения в определенном порядке действий сложения, вычитания и умножения. Целые рациональные функции входят в более широкий класс рациональных функций, где к перечисленным действиям: присоединяется деление: любую рациональную функцию можно представить в виде частного двух М. Наконец, рациональные функции содержатся в классе алгебраических функций.