"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МНОГОМЕРНЫЙ УЗЕЛ
Значение МНОГОМЕРНЫЙ УЗЕЛ в математической энциклопедии:
- изотопический класс вложений сферы в сферу. Более точно, re-мерным узлом коразмерности q наз. пара  , состоящая из ориентированной сферы
, состоящая из ориентированной сферы  и ее ориентированного локально плоского подмногообразия
и ее ориентированного локально плоского подмногообразия  , гомеоморфного сфере
, гомеоморфного сфере  . Два узла
. Два узла  наз. эквивалентными, если существует изотопия сферы
наз. эквивалентными, если существует изотопия сферы  , переводящая
, переводящая  на
на  с сохранением ориентации. В зависимости от того, в какой категории (Diff, PL или Тор) понимаются термины "подмногообразие" и "изотопия" в предыдущих определениях, говорится о гладких, кусочно линейных пли топо-логич. М. у. соответственно. В гладком случае подмногообразие
с сохранением ориентации. В зависимости от того, в какой категории (Diff, PL или Тор) понимаются термины "подмногообразие" и "изотопия" в предыдущих определениях, говорится о гладких, кусочно линейных пли топо-логич. М. у. соответственно. В гладком случае подмногообразие  может иметь п нестандартную дифференцируемую структуру, n-мерный узел коразмерности q, изотопный стандартному вложению, наз. тривиальным, или незаузленным, узлом.
может иметь п нестандартную дифференцируемую структуру, n-мерный узел коразмерности q, изотопный стандартному вложению, наз. тривиальным, или незаузленным, узлом.
Изучение М. у. коразмерности 1 связано с Шёнфлиса гипотезой. Всякий топологич. узел коразмерности 1 тривиален. Это же верно и для кусочно линейных и гладких узлов, если 
Кусочно линейные и тоиологич. М. у. коразмерности  тривиальны. В гладком случае это не так. Множество изотопич. классов гладких га-мерных узлов коразмерности
тривиальны. В гладком случае это не так. Множество изотопич. классов гладких га-мерных узлов коразмерности  совпадает при
совпадает при  с множеством
с множеством  классов кобордизмов узлов (два М. у.
классов кобордизмов узлов (два М. у. =
= наз. кобордантными, если существует гладкое
наз. кобордантными, если существует гладкое  -мерное подмногообразие
-мерное подмногообразие  , трансверсально выходящее на
, трансверсально выходящее на  , причем
, причем  и
и  является h-кобордизмом между
является h-кобордизмом между  ). Множество
). Множество  является абелевой группой относительно связного суммирования. В этой группе противоположным к классу М. у.
является абелевой группой относительно связного суммирования. В этой группе противоположным к классу М. у.  является класс кобордизмов узла
является класс кобордизмов узла  , где минус означает обращение ориентации. Имеется естественный гомоморфизм
, где минус означает обращение ориентации. Имеется естественный гомоморфизм 
 , где
, где  - группа n -мерных гомотопич. сфер; этот гомоморфизм сопоставляет узлу
- группа n -мерных гомотопич. сфер; этот гомоморфизм сопоставляет узлу 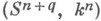 дифференцируемую структуру сферы
дифференцируемую структуру сферы  . Ядро этого гомоморфизма, обозначаемое
. Ядро этого гомоморфизма, обозначаемое  , совпадает с множеством изотопич. классов стандартной сферы
, совпадает с множеством изотопич. классов стандартной сферы  в
в  . Если
. Если  то группа
то группа  тривиальна. Если
тривиальна. Если 
 , то группы
, то группы  и
и  конечны. В случае, когда
конечны. В случае, когда  , группы
, группы  и
и  являются конечно порожденными абелевыми группами ранга 1 (см. [1], [2]). Вычислено также множество классов конкордантных гладких вложений
являются конечно порожденными абелевыми группами ранга 1 (см. [1], [2]). Вычислено также множество классов конкордантных гладких вложений  в
в  при
при  (см. [3]).
(см. [3]).
Изучение М. у. коразмерности 2, к-рые в дальнейшем будут наз. просто узлами, проходит почти аналогично во всех трех категориях (Diff, Pl, Top). При  всякий топология, узел переводится изотопией в гладкий. Однако существуют топологич. трехмерные узлы в
всякий топология, узел переводится изотопией в гладкий. Однако существуют топологич. трехмерные узлы в  , не эквивалентные и даже не кобордантные гладким узлам (см. [4]).
, не эквивалентные и даже не кобордантные гладким узлам (см. [4]).
Множество изотопич. классов re-мерных узлов (каждой категории) образует абелеву полугруппу относительно связного суммирования. Известно, что при n= 1 в этой полугруппе всякий элемент представляется в виде конечной суммы простых, т. е. нетривиальным образом неразложимых элементов, и такое разложение единственно n -мерный узел  тривиален тогда и только тогда, когда
тривиален тогда и только тогда, когда 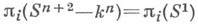 при всех
при всех  Дана (см. [6]) алгебраич. классификация узлов К, у к-рых
Дана (см. [6]) алгебраич. классификация узлов К, у к-рых  при всех
при всех  и число пнечетно (узлы типа L):при n>=5 множество изотопич. классов таких узлов находится во взаимно однозначном соответствии с множеством S-эквивалентных классов Зейферта матриц. Узлы типа Lважны с точки зрения приложений в алгебраич. геометрии, т. к. среди них находятся все узлы, получаемые с помощью следующей конструкции (см. [15]). Пусть
и число пнечетно (узлы типа L):при n>=5 множество изотопич. классов таких узлов находится во взаимно однозначном соответствии с множеством S-эквивалентных классов Зейферта матриц. Узлы типа Lважны с точки зрения приложений в алгебраич. геометрии, т. к. среди них находятся все узлы, получаемые с помощью следующей конструкции (см. [15]). Пусть  - комплексный многочлен ненулевой степени, имеющий О в качестве изолированной особой точки и f(0)=0. Пересечение кгиперповерхности
- комплексный многочлен ненулевой степени, имеющий О в качестве изолированной особой точки и f(0)=0. Пересечение кгиперповерхности  с малой сферой
с малой сферой 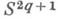 с центром в нуле является (q-2)-связным
с центром в нуле является (q-2)-связным  -мерным многообразием. Многообразие кгомеоморфно сфере
-мерным многообразием. Многообразие кгомеоморфно сфере  тогда и только тогда, когда
тогда и только тогда, когда 
 , где
, где  - полином Александера. Вэтом случае возникает узел
- полином Александера. Вэтом случае возникает узел  . Такие узлы наз. алгебраическими, все они являются узлами типа L.
. Такие узлы наз. алгебраическими, все они являются узлами типа L.
Внешностью гладкого узла  наз. дополнение Xоткрытой трубчатой окрестности
наз. дополнение Xоткрытой трубчатой окрестности  в
в 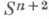 . При
. При  для всякого га-мерного узла Ксуществует такой узел
для всякого га-мерного узла Ксуществует такой узел  , что всякий узел, внешность к-ро-го диффеоморфна внешности узла К, эквивалентен либо К, либо
, что всякий узел, внешность к-ро-го диффеоморфна внешности узла К, эквивалентен либо К, либо  . Если
. Если  - внешности двух гладких n -мерных узлов,
- внешности двух гладких n -мерных узлов, то следующие утверждения равносильны (см. [7]): 1)
то следующие утверждения равносильны (см. [7]): 1) и
и  диффеоморфны, 2) пары
диффеоморфны, 2) пары  гомотопически эквивалентны. Эти результаты сводят проблему классификации узлов к гомотопич. классификации пар
гомотопически эквивалентны. Эти результаты сводят проблему классификации узлов к гомотопич. классификации пар  и к решению вопроса о том, определяет ли внешность тип узла, т. е. верно ли равенство
и к решению вопроса о том, определяет ли внешность тип узла, т. е. верно ли равенство 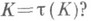 Известно, что это равенство справедливо для узлов типа L(см. [6]), для узлов, получаемых конструкцией Артина и конструкцией сверхзакручивания (см. [8]). Однако найдены двумерные узлы в
Известно, что это равенство справедливо для узлов типа L(см. [6]), для узлов, получаемых конструкцией Артина и конструкцией сверхзакручивания (см. [8]). Однако найдены двумерные узлы в 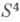 , для к-рых
, для к-рых 
 . (см. [9]).
. (см. [9]).
Изучение гомотопич. типа внешности X усложняется из-за ее неодносвязности. Если G- группа узла (т. е.  ), то
), то  ,
,  , вес группы G(т. е. минимальное число элементов, не содержащихся ни в одном собственном нормальном делителе) равен 1. При
, вес группы G(т. е. минимальное число элементов, не содержащихся ни в одном собственном нормальном делителе) равен 1. При  эти свойства полностью описывают класс групп n -мерных узлов (см. [10]). Группы одномерных и двумерных узлов обладают рядом дополнительных свойств (см. Узлов теория, Двумерный, узел).
эти свойства полностью описывают класс групп n -мерных узлов (см. [10]). Группы одномерных и двумерных узлов обладают рядом дополнительных свойств (см. Узлов теория, Двумерный, узел).
Поскольку  внешность Xобладает единственным бесконечным циклическим накрытием
внешность Xобладает единственным бесконечным циклическим накрытием  , к-рое наз. бесконечным циклическим накрытием узла. Гомологии
, к-рое наз. бесконечным циклическим накрытием узла. Гомологии  являются
являются  -модулями. Их Александера инвариан ты, являются инвариантами узла. Об алгебраич. свойствах модулей
-модулями. Их Александера инвариан ты, являются инвариантами узла. Об алгебраич. свойствах модулей  см. [10]-[13].
см. [10]-[13].
Благодаря тому обстоятельству, что на бесконечном циклическом накрытии группа  действует без неподвижных точек, (n+2)-мерное некомпактное многообразие
действует без неподвижных точек, (n+2)-мерное некомпактное многообразие  обладает рядом гомология, свойств компактных (га+1)-мерных многообразий. В частности, на гомоло-гиях многообразия
обладает рядом гомология, свойств компактных (га+1)-мерных многообразий. В частности, на гомоло-гиях многообразия 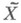 с коэффициентами в поле Fсуществует невырожденное спаривание
с коэффициентами в поле Fсуществует невырожденное спаривание

по свойствам напоминающее спаривание, определяемое пересечения индексом в (n+1)-мерных компактных многообразиях. Имеется также спаривание

аналогичное зацепления коэффициентам в (n+1) - мерных многообразиях (см. [13]), где 
Эти гомологич. спаривания порождают инварианты гомотопич. типа пары  . Для получения алгебраич. инвариантов используются также конечнолистные циклические разветвленные накрытия (см. [14]).
. Для получения алгебраич. инвариантов используются также конечнолистные циклические разветвленные накрытия (см. [14]).
Задача классификации узлов коразмерности 2 с точностью до кобордизма - отношения эквивалентности более грубого, чем изотопич. тип,- полностью решена при 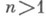 (см. Узлов кобордизм).
(см. Узлов кобордизм).
Лит.:[11 Haefliger A., "Ann. Math.", 1962, v. 75, p. 452-66; [2] eго же, там же, 1966, v. 83, р. 402-36; [3] Levine J., там же, 1965, v. 82, р. 15-51; [4] Сарреll S. Shaneson J., "Topology", 1973, v. 12, p. 33-40; [5] Соси нский А. Б., "Матем. сб.", 1970, т. 81, № 1, с. 145-58-[6] Levine J., "Comm. math, helv.", 1970, v. 45, p. 185-98; [7] Lashof R., Shaneson J., "Bull. Amer. Math. Soc", 1969, v. 75, p. 171-75; |8] Cappell S., в кн.: Topology of Manifolds, Chi., 1971, p. 358-83; [9] Сappell S., Shaneson J., "Ann. Math.", 1976, v. 103, p. 349-53; [10] Кеrvaire M., "Bull. soc. math. France", 1965, t. 93, p. 225-71; [111 Levine J., "Ann. Math.", 1966, v. 84, p. 537-54; [12] его ж е, в кн.: Knots, groups and 3-manifolds, Princeton, 1975, p. 25- 34; [13] Фарбер М. Ш., "Изв. АН СССР. Сер. матем.", 1977, т. 41, с. 794-828; [14] Виро О. Я., там же, 1973, т. 37, с. 1241-58; [15] Милнор Дж., Особые точки комплексных гиперповерхностей, пер. <сангл., М.,1971. М. Ш. Фарбер.

 , состоящая из ориентированной сферы
, состоящая из ориентированной сферы  и ее ориентированного локально плоского подмногообразия
и ее ориентированного локально плоского подмногообразия  , гомеоморфного сфере
, гомеоморфного сфере  . Два узла
. Два узла  наз. эквивалентными, если существует изотопия сферы
наз. эквивалентными, если существует изотопия сферы  , переводящая
, переводящая  на
на  с сохранением ориентации. В зависимости от того, в какой категории (Diff, PL или Тор) понимаются термины "подмногообразие" и "изотопия" в предыдущих определениях, говорится о гладких, кусочно линейных пли топо-логич. М. у. соответственно. В гладком случае подмногообразие
с сохранением ориентации. В зависимости от того, в какой категории (Diff, PL или Тор) понимаются термины "подмногообразие" и "изотопия" в предыдущих определениях, говорится о гладких, кусочно линейных пли топо-логич. М. у. соответственно. В гладком случае подмногообразие  может иметь п нестандартную дифференцируемую структуру, n-мерный узел коразмерности q, изотопный стандартному вложению, наз. тривиальным, или незаузленным, узлом.
может иметь п нестандартную дифференцируемую структуру, n-мерный узел коразмерности q, изотопный стандартному вложению, наз. тривиальным, или незаузленным, узлом.
 тривиальны. В гладком случае это не так. Множество изотопич. классов гладких га-мерных узлов коразмерности
тривиальны. В гладком случае это не так. Множество изотопич. классов гладких га-мерных узлов коразмерности  совпадает при
совпадает при  с множеством
с множеством  классов кобордизмов узлов (два М. у.
классов кобордизмов узлов (два М. у. =
= наз. кобордантными, если существует гладкое
наз. кобордантными, если существует гладкое  -мерное подмногообразие
-мерное подмногообразие  , трансверсально выходящее на
, трансверсально выходящее на  , причем
, причем  и
и  является h-кобордизмом между
является h-кобордизмом между  ). Множество
). Множество  является абелевой группой относительно связного суммирования. В этой группе противоположным к классу М. у.
является абелевой группой относительно связного суммирования. В этой группе противоположным к классу М. у.  является класс кобордизмов узла
является класс кобордизмов узла  , где минус означает обращение ориентации. Имеется естественный гомоморфизм
, где минус означает обращение ориентации. Имеется естественный гомоморфизм 
 , где
, где  - группа n -мерных гомотопич. сфер; этот гомоморфизм сопоставляет узлу
- группа n -мерных гомотопич. сфер; этот гомоморфизм сопоставляет узлу 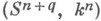 дифференцируемую структуру сферы
дифференцируемую структуру сферы  . Ядро этого гомоморфизма, обозначаемое
. Ядро этого гомоморфизма, обозначаемое  , совпадает с множеством изотопич. классов стандартной сферы
, совпадает с множеством изотопич. классов стандартной сферы  в
в  . Если
. Если  то группа
то группа  тривиальна. Если
тривиальна. Если 
 , то группы
, то группы  и
и  конечны. В случае, когда
конечны. В случае, когда  , группы
, группы  и
и  являются конечно порожденными абелевыми группами ранга 1 (см. [1], [2]). Вычислено также множество классов конкордантных гладких вложений
являются конечно порожденными абелевыми группами ранга 1 (см. [1], [2]). Вычислено также множество классов конкордантных гладких вложений  в
в  при
при  (см. [3]).
(см. [3]). всякий топология, узел переводится изотопией в гладкий. Однако существуют топологич. трехмерные узлы в
всякий топология, узел переводится изотопией в гладкий. Однако существуют топологич. трехмерные узлы в  , не эквивалентные и даже не кобордантные гладким узлам (см. [4]).
, не эквивалентные и даже не кобордантные гладким узлам (см. [4]). тривиален тогда и только тогда, когда
тривиален тогда и только тогда, когда 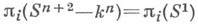 при всех
при всех  Дана (см. [6]) алгебраич. классификация узлов К, у к-рых
Дана (см. [6]) алгебраич. классификация узлов К, у к-рых  при всех
при всех  и число пнечетно (узлы типа L):при n>=5 множество изотопич. классов таких узлов находится во взаимно однозначном соответствии с множеством S-эквивалентных классов Зейферта матриц. Узлы типа Lважны с точки зрения приложений в алгебраич. геометрии, т. к. среди них находятся все узлы, получаемые с помощью следующей конструкции (см. [15]). Пусть
и число пнечетно (узлы типа L):при n>=5 множество изотопич. классов таких узлов находится во взаимно однозначном соответствии с множеством S-эквивалентных классов Зейферта матриц. Узлы типа Lважны с точки зрения приложений в алгебраич. геометрии, т. к. среди них находятся все узлы, получаемые с помощью следующей конструкции (см. [15]). Пусть  - комплексный многочлен ненулевой степени, имеющий О в качестве изолированной особой точки и f(0)=0. Пересечение кгиперповерхности
- комплексный многочлен ненулевой степени, имеющий О в качестве изолированной особой точки и f(0)=0. Пересечение кгиперповерхности  с малой сферой
с малой сферой 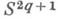 с центром в нуле является (q-2)-связным
с центром в нуле является (q-2)-связным  -мерным многообразием. Многообразие кгомеоморфно сфере
-мерным многообразием. Многообразие кгомеоморфно сфере  тогда и только тогда, когда
тогда и только тогда, когда 
 , где
, где  - полином Александера. Вэтом случае возникает узел
- полином Александера. Вэтом случае возникает узел  . Такие узлы наз. алгебраическими, все они являются узлами типа L.
. Такие узлы наз. алгебраическими, все они являются узлами типа L. наз. дополнение Xоткрытой трубчатой окрестности
наз. дополнение Xоткрытой трубчатой окрестности  в
в 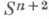 . При
. При  для всякого га-мерного узла Ксуществует такой узел
для всякого га-мерного узла Ксуществует такой узел  , что всякий узел, внешность к-ро-го диффеоморфна внешности узла К, эквивалентен либо К, либо
, что всякий узел, внешность к-ро-го диффеоморфна внешности узла К, эквивалентен либо К, либо  . Если
. Если  - внешности двух гладких n -мерных узлов,
- внешности двух гладких n -мерных узлов, то следующие утверждения равносильны (см. [7]): 1)
то следующие утверждения равносильны (см. [7]): 1) и
и  диффеоморфны, 2) пары
диффеоморфны, 2) пары  гомотопически эквивалентны. Эти результаты сводят проблему классификации узлов к гомотопич. классификации пар
гомотопически эквивалентны. Эти результаты сводят проблему классификации узлов к гомотопич. классификации пар  и к решению вопроса о том, определяет ли внешность тип узла, т. е. верно ли равенство
и к решению вопроса о том, определяет ли внешность тип узла, т. е. верно ли равенство 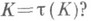 Известно, что это равенство справедливо для узлов типа L(см. [6]), для узлов, получаемых конструкцией Артина и конструкцией сверхзакручивания (см. [8]). Однако найдены двумерные узлы в
Известно, что это равенство справедливо для узлов типа L(см. [6]), для узлов, получаемых конструкцией Артина и конструкцией сверхзакручивания (см. [8]). Однако найдены двумерные узлы в 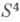 , для к-рых
, для к-рых 
 . (см. [9]).
. (см. [9]). ), то
), то  ,
,  , вес группы G(т. е. минимальное число элементов, не содержащихся ни в одном собственном нормальном делителе) равен 1. При
, вес группы G(т. е. минимальное число элементов, не содержащихся ни в одном собственном нормальном делителе) равен 1. При  эти свойства полностью описывают класс групп n -мерных узлов (см. [10]). Группы одномерных и двумерных узлов обладают рядом дополнительных свойств (см. Узлов теория, Двумерный, узел).
эти свойства полностью описывают класс групп n -мерных узлов (см. [10]). Группы одномерных и двумерных узлов обладают рядом дополнительных свойств (см. Узлов теория, Двумерный, узел). внешность Xобладает единственным бесконечным циклическим накрытием
внешность Xобладает единственным бесконечным циклическим накрытием  , к-рое наз. бесконечным циклическим накрытием узла. Гомологии
, к-рое наз. бесконечным циклическим накрытием узла. Гомологии  являются
являются  -модулями. Их Александера инвариан ты, являются инвариантами узла. Об алгебраич. свойствах модулей
-модулями. Их Александера инвариан ты, являются инвариантами узла. Об алгебраич. свойствах модулей  см. [10]-[13].
см. [10]-[13]. действует без неподвижных точек, (n+2)-мерное некомпактное многообразие
действует без неподвижных точек, (n+2)-мерное некомпактное многообразие  обладает рядом гомология, свойств компактных (га+1)-мерных многообразий. В частности, на гомоло-гиях многообразия
обладает рядом гомология, свойств компактных (га+1)-мерных многообразий. В частности, на гомоло-гиях многообразия 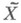 с коэффициентами в поле Fсуществует невырожденное спаривание
с коэффициентами в поле Fсуществует невырожденное спаривание


 . Для получения алгебраич. инвариантов используются также конечнолистные циклические разветвленные накрытия (см. [14]).
. Для получения алгебраич. инвариантов используются также конечнолистные циклические разветвленные накрытия (см. [14]).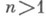 (см. Узлов кобордизм).
(см. Узлов кобордизм).