|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МНОГОМЕРНАЯ ВАРИАЦИОННАЯ ЗАДАЧАЗначение МНОГОМЕРНАЯ ВАРИАЦИОННАЯ ЗАДАЧА в математической энциклопедии: вариационная задача с частными производными,- задача вариационного исчисления, в к-рой требуется определить экстремум функционала, зависящего от функций многих независимых переменных. Обычные вариационные задачи, в к-рых рассматриваются функционалы от функций одной независимой переменной, можно назвать в этом смысле одномерными вариационными задачами. Примером двумерной вариационной задачи может служить задача, в к-рой требуется определить функцию двух независимых переменных u(x, y), непрерывную вместе со своими частными производными 1-го порядка, доставляющую экстремум функционалу
при граничном условии
где I- замкнутый контур, ограничивающий область D
Если
Уравнение (4) наз. уравнением Эйлера - Остроградского (иногда - уравнением Остроградского). Этому уравнению должна удовлетворять функция В случае тройного интеграла и функции
Следующее условие является аналогом Лежандра условия. Для того чтобы функция
Для минимума необходимо
Рассматриваются также разрывные М. в. з. (см. [4]). Лит.:[1] Курант Р., Гильберт Д., Методы математической физики, пер. с нем., 2 изд., т. 2, М.- Л., 1951; [2] Смирнов В. И., Курс высшей математики, 5 изд., т. 4, М., 1958; [3] Ахиезер Н. И., Лекции по вариационному исчислению, М., 1955; [4] Керимов М. К., "Тр. Тбилисск. матем. ин-та АН Груз. ССР", 1951, т. 18, с. 209 - 19. И. Б. Вапнярский. |
|
|
|



 - заданная функция,
- заданная функция, - дважды непрерывно дифференцируемая функция по совокупности своих аргументов. Пусть и( х, у )есть решение задачи (1), (2). Подстановка функций сравнения
- дважды непрерывно дифференцируемая функция по совокупности своих аргументов. Пусть и( х, у )есть решение задачи (1), (2). Подстановка функций сравнения 
 - числовой параметр, в функционал (1), дифференцирование по
- числовой параметр, в функционал (1), дифференцирование по 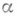 и приравнивание
и приравнивание  позволяет получить следующее выражение для первой вариации функционала
позволяет получить следующее выражение для первой вариации функционала
 имеет непрерывные производные 2-го порядка, то легко показать, что необходимым условием равенства нулю первой вариации
имеет непрерывные производные 2-го порядка, то легко показать, что необходимым условием равенства нулю первой вариации  является выполнение условия
является выполнение условия
 , доставляющая экстремум функционалу (1) при граничных условиях (2). Уравнение Эйлера - Остроградского является аналогом уравнения Эйлера для одномерных вариационных задач. В развернутом виде (4) представляет собой уравнение с частными производными 2-го порядка.
, доставляющая экстремум функционалу (1) при граничных условиях (2). Уравнение Эйлера - Остроградского является аналогом уравнения Эйлера для одномерных вариационных задач. В развернутом виде (4) представляет собой уравнение с частными производными 2-го порядка. , зависящей от трех независимых переменных, уравнение Эйлера - Остроградского принимает вид:
, зависящей от трех независимых переменных, уравнение Эйлера - Остроградского принимает вид:
 доставляла хотя бы слабый экстремум функционалу (1), необходимо, чтобы в каждой внутренней точке области Dвыполнялось условие
доставляла хотя бы слабый экстремум функционалу (1), необходимо, чтобы в каждой внутренней точке области Dвыполнялось условие
 , а для максимума
, а для максимума
