Математический словарь
|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МНОГОЛИСТНАЯ ОБЛАСТЬЗначение МНОГОЛИСТНАЯ ОБЛАСТЬ в математической энциклопедии: - область S римановой поверхности R, рассматриваемой как накрывающая поверхность над плоскостью комплексного переменного Для аналитич. функций многих комплексных переменных также возникают многолистные римановы области над комплексным пространством Е. Д. Соломенцев. |
|
|
|

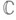 , такая, что над каждой точкой ее проекции
, такая, что над каждой точкой ее проекции  расположены не менее двух точек S; ветвления точка R порядка
расположены не менее двух точек S; ветвления точка R порядка  считается при этом за kточек. Напр., аналитич. функция
считается при этом за kточек. Напр., аналитич. функция  отображает взаимно однозначно круг
отображает взаимно однозначно круг  на двулистную область (двулистный круг)
на двулистную область (двулистный круг) римановой поверхности Вэтой функции; всюду, кроме начала координат, это отображение конформно.
римановой поверхности Вэтой функции; всюду, кроме начала координат, это отображение конформно.