|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МНОГОЗНАЧНАЯ ЛОГИКАЗначение МНОГОЗНАЧНАЯ ЛОГИКА в математической энциклопедии: - раздел математической логики, изучающий математич. модели логики высказываний. Эти модели отражают две основные черты последней - множественность значений истинности высказываний и возможность построения новых более сложных высказываний из заданных при помощи логич. операций, к-рые позволяют также по значениям истинности исходных высказываний устанавливать значение истинности сложного высказывания. Примерами многозначных высказываний являются суждения с модальным исходом ("да", "нет", "может быть") и суждения вероятностного характера, а примерами логич. операций - логич. связки типа "и", "пли", "если..., то". В общем случае модели М. л. представляют собой обобщения алгебры логики. Важно отметить, что в алгебре логики высказывания принимают только два значения истинности ("да", "нет"), в связи с чем она в общем случае не может отразить всего многообразия логпч. построений, встречающихся на практике. При достаточно широком толковании М. л. в нее иногда включают также логические исчисления. Исторически первыми моделями М. л. явились двузначная логика Дж. Буля (G. Boole, сер. 19 в.), называемая также алгеброй логики, трехзначная логика Я. Лукасевича (J. tucasiewicz, 1920) и m-значная логика Э. Поста (Е. Post, 1921). Изучение этих моделей составило важный этап в создании теории М. л. Основные модели многозначной логики. М. л. обладает определенной спецификой, состоящей в рассмотрении задач и подходов, возникающих при исследовании М. л. с позиций математич. логики, математич. кибернетики и алгебры. Так, с позиций математич. кибернетики модели М. л. рассматриваются как языки, описывающие функционирование сложных управляющих систем, компоненты к-рых могут находиться в нек-ром числе различных состояний, а с точки зрения алгебры модели М. л. представляют алгебраические системы, имеющие наряду с прикладным и теоретич. интерес. Построение моделей М. л. осуществляется по, аналогии с построением двузначной логики. Так, индивидуальные высказывания логики, разбитые на классы с одним и тем же значением истинности, приводят к понятию множества Е- констант модели, к-рые фактически отождествляют все индивидуальные высказывания, заменяя их соответствующими значениями истинности; переменные высказывания приводят к переменным величинам х 1 , х 2, ..., которые в качестве значений принимают элементы из множества Е;. логич. связки приводят к множеству Мэлементарных функций (операций), к-рые, как и их аргументы, принимают значения из Е. Сложные высказывания, построенные из индивидуальных и переменных высказываний, а также логич. связок, приводят к множеству Своеобразие подхода математич. кибернетики к М. л. состоит в рассмотрении моделей М. л. как управляющих систем. Элементарные функции при этом являются элементами, производящими определенные операции, а формулы интерпретируются как схемы, построенные из элементов и также осуществляющие переработку входной информации в выходную. Такого рода управляющие системы, известные в кибернетике как схемы из функциональных элементов (без ветвления), широко используются в теоретич. и практич. вопросах кибернетики. Вместе с тем существует ряд задач логики н кибернетики, к-рый связан с изучением соответствий между множествами Ми [М]и при к-ром роль множества <М> несколько затушевывается, сводясь к способу определения второго множества по первому. В этом случае приходят к другой модели М. л., представляющей собой алгебру, элементами к-рой являются функции, принимающие в качестве значений, как и их аргументы, элементы из Е. В качестве операций в этих алгебрах обычно используется специальный набор операций, эквивалентный в смысле соответствий Ми [М]множеству формул, построенных из функций множества М, т. е. получению сложных функций из заданных путем подстановки одних функций вместо аргументов других. Эти алгебры наз. алгебрами m-значных логик. Конкретно это может быть достигнуто, напр., введением следующих унарных операций:
если
и для
Возникающие алгебры Проблематика многозначной логики. К числу задач, характерных для формульной модели М. л., относится задача "об описании", т. е. вопрос об указании для заданного множества Пограничным вопросом между математич. логикой и алгеброй, примыкающим к задаче об описании, является задача о тождественных преобразованиях. В ней при заданном множестве Мтребуется выделить в нек-ром смысле простейшее подмножество пар равных, т. е. реализующих одну и ту же функцию, формул из Аналогичное место занимает т. н. проблема полноты, состоящая в указании всех таких подмножеств Глобальной задачей для М. л. является описание решетки замкнутых классов данной модели М. л. Характерный для теории управляющих систем вопрос о сложности этих систем естественно возникает и по отношению к формулам и функциям из М. л. Типичной при таком подходе является следующая задача о сложности реализации. На множестве всех элементарных формул нек-рым способом вводится числовая мера (сложность формул), к-рая затем распространяется на множество всех формул, напр, путем суммирования мер всех тех элементарных формул, к-рые участвуют в построении заданной формулы. Требуется для заданной функции указать ту формулу (простейшую), к-рая реализует эту функцию и имеет наименьшую сложность, а также выяснить, как эта сложность зависит от нек-рых свойств рассматриваемой функции. Исследуются различные обобщения этой задачи. Широкий круг вопросов связан с реализацией функций формулами с наперед заданными свойствами. Сюда относятся задача о реализации функций алгебры логики дизъюнктивными нормальными формами и связанная с этим задача минимизации; а также задача о реализации функций формулами в нек-ром смысле ограниченной глубины (т. е. такими формулами, в к-рых цепочка подставляемых друг в друга формул имеет ограниченную длину, такое ограничение связано с надежностью и скоростью вычислений), задача о декомпозиций, т. е. о реализации функций от переменных при помощи формул, построенных из элементарных формул, реализующих функции от меньшего числа переменных, и ряд других. Решения всех перечисленных выше задач существенно зависят от мощности множества Еи множества М, порождающего заданную модель М. л. Важнейшие примеры многозначных логик. К числу наиболее важных примеров М. л. относятся конечно-значные логики (т. е. m-значные логики, для к-рых тконечно). Для них обычно полагают, что Е=Е т={0, 1, ... , т-1}, а m-значную логику MF обозначают М т . Наиболее глубоко исследован случай т=2, при этом функции двузначной логики наз. также булевыми функциями. Важнейшим результатом здесь является полное описание Э. Постом (Е. Post, см. [1]) решетки замкнутых классов. Множество их оказалось счетным, а каждый класс и решетки их по включению строятся эффективно. Эти классы наз. классами Поста. Всякий замкнутый класс имеет конечный базис, и его мощность не превосходит 4. Из этих результатов получаются решения задач о выразимости, полноте и базисах, а также задачи о тождественных преобразованиях. Относительно полных конечных систем для "почти всех" функций указано поведение меры сложности простейших формул, реализующих эти функции, и построен соответствующий алгоритм синтеза формул (см. [2]). Изучены задачи о построении оптимальных по сложности формул, реализующих функции надежно и достаточно хорошо по быстродействию, а также вопросы сложности реализации для большого числа специальных классов функций и отдельных функций. Одним из глубоко исследованных вопросов для двузначной логики является также задача минимизации. В ней изучается специальный язык задания функций двузначной логики - язык дизъюнктивных нормальных форм (д. н. ф.). Вводится понятие сложности д. н. ф.- число букв в ней - и изучаются задачи поиска, строения и метрич. свойств "простейших" в смысле этой меры д. н. ф., реализующих заданную функцию (см. [3]). Задача о декомпозиции для булевых функций состоит в выяснении условий, при к-рых заданная функция от ппеременных может быть реализована формулой, построенной из функций от меньшего числа переменных, причем все функции, подставляемые друг в друга в процессе построения формулы, не зависят от общих переменных. Такие формулы наз. бесповторными. Показано, что не существует конечной системы функций такой, что каждая функция может быть реализована бесповторной формулой над этой системой, и даже что "почти все" функции не допускают реализации бесповторными формулами. В целом двузначные логики, в силу нек-рых их особенностей, являются главным объектом, на к-ром просматриваются общие постановки задач. Для произвольных конечнозначных логик, к-рые при m>2 существенно отличаются от двузначной логики, имеются эффективные решения задач о выразимости для конечных систем. Показано, что при Особый интерес представляет задача о полноте в т- значной логике Р т. В Р т существуют конечные полные системы, что позволяет из каждой полной системы выделить конечную полную подсистему и свести задачу к изучению полноты конечных систем. Существуют также полные системы, состоящие из одной функции, такие функции наз. шефферовыми. Примером их может служить функция Вебба mах (x1, х 2)+l (mod m). В силу конечной порожденности в Р т эффективно решается задача о полноте. В Р т явно построены все предполные классы, являющиеся классами сохранения специальных предикатов. Указание этих предикатов составляет содержание теоремы о полноте в конечнозначных логиках (см. [7]). Говорят, что функция f {х 1,... , х п )сохраняет предикат R:(Em )h Ю{0, 1}, если формула
тождественно равна 1 при всех значениях переменных Семейство Uсостоит из всех предикатов R(y1,... , yh )таких, что при Для систем, состоящих из одной функции, критерием полноты является условие 2-транзитивности. Произвольное множество функций при m>2 является полным тогда и только тогда, когда оно m-транзитивно и степень транзитивности не может быть понижена. От конечных полных систем путем операции отождествления можно перейти к рассмотрению более простого класса полных систем, наз. простыми базисами. Под простым базисом понимается такая конечная полная система, к-рая теряет свойство полноты после отождествления любой пары существенных переменных у любой функции этой системы. Существует лишь конечное число qпростых базисов и Первыми примерами конечнозначных логик явились трехзначная логика Лукасевича, к-рая порождается функциями 1- х,min(l, 1- х 1+х 2 ), где х 1, х 2 принимают значения 0, 1/2, 1, и т- значная логика Поста, к-рая порождается функциями х 2+1(mod m),max (x1 , x2), где х 1 , х 2 принимают значения 0, 1, ... , т-1. К конечно-значным логикам примыкают алгебры многозначных функций, на которые в значительной мере переносятся проблематика и методы исследования конечнозначных логик. Примерами других М. л. являются счетнозначные и континуумзначные логики (т. е. такие m-значные логики, для к-рых мощность тявляется соответственно счетной или континуальной). Эти модели играют важную роль в математич. логике, теории моделей и в ма-тематич. анализе. Для счетнозначных логик установлена гиперконтинуальность множеств предполных (а значит и множества всех) замкнутых классов и найдено решение задачи о полноте систем, содержащих множество В счетнозначных и контннуумзначных логиках особую роль играют различные их подклассы. Таковыми являются в первом случае предельные логики, а во втором - М. л. непрерывных функций. Предельные логики представляют собой счетные замкнутые классы функций М. л. К М. л. могут быть отнесены также и такие алгебры функций, в к-рых запас операций несколько отличается от описанного выше. Таковы алгебры неоднородных конечнозначных функций (их аргументы принимают конечное число значений из своих областей), рекурсивных и частично-рекурсивных функций, алгебры автоматных отображений и ряд других. Лит.:[1] Яблонский С. В., Гаврилов Г. П., Кудрявцев В. Б., Функции алгебры логики и классы Поста, М., 1906; [2] Лупанов О. Б., "Проблемы кибернетики", 1965, в. 14, с. 31 - 110; [3] Журавлев Ю. И., "Проблемы кибернетики", 1962, в. 8, с. 5-44: [4] Линдон Р. К., "Кибернетич. сб.", 1960, в. 1, с. 234-45: [5] Мурский В. Л., "Докл. АН СССР", 1965,т. 163, № 4, с. 815-18; [6] Янов Ю. И., Мучник А. А., "Докл. АН СССР", 1959, т. 127, №1, с. 44- 46; [7] Rоsenberg J., Uber die funktionale Vollstandigkeit in den mehrwertigen Logikcn, Praha, 1970; [8]3axapова Е. Ю., Кудрявцев В. Б., Яблонский С. В., "Докл. АН СССР", 1969", т. 186, № 3, с. 509-12; [9] Яблонский С. В., "Тр. Матем. ин-та АН СССР", 1958, т. 51, с. 5 - 142; [10] Саломаа А., "Кибернетич. сб. ", 1964, в. 8, с. 7-32; [11] Кудрявцев В. Б., "Elektronische Informationsverarbeitung und Kybernetik" (EIK), 1973, Bd 9, Hit 1/2, S. 81 -105; [12] Алексеев В. Б., "Дискретный анализ", 1971, № 19, с. 3-10; [13] Мальцев А. И., "Алгебра и логика", 1966, т. 5, в. 2, с. 5-24; [14] Гаврилов Г. П., "Проблемы кибернетики", 1965, в. 15, с. 5-64; [151 Деметрович Я., "Проблемы кибернетики", 1975, в. 30, с. 5 - 42; [16] Витушкин А. Г., в кн.: Тр. Международного конгресса математиков, М., 1968, с. 322- 28. В. Б. Кудрявцев. |
|
|
|

 формул над М. Значение истинности из Есложного высказывания является функцией от соответствующих значений истинности высказываний, входящих в данное сложное высказывание. В модели эта функция приписывается формуле, соответствующей данному сложному высказыванию; говорят также, что формула реализует эту функцию. Функции, отображающие кортежи элементов из Ев Е, наз. функциями т- значной логики, где тобозначает мощность множества Е. Множество всех функций m-значной логики обозначают через Р т . Множество формул
формул над М. Значение истинности из Есложного высказывания является функцией от соответствующих значений истинности высказываний, входящих в данное сложное высказывание. В модели эта функция приписывается формуле, соответствующей данному сложному высказыванию; говорят также, что формула реализует эту функцию. Функции, отображающие кортежи элементов из Ев Е, наз. функциями т- значной логики, где тобозначает мощность множества Е. Множество всех функций m-значной логики обозначают через Р т . Множество формул 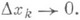 приводит к множеству [М]функций, реализуемых формулами из
приводит к множеству [М]функций, реализуемых формулами из  и наз. суперпозиция м и (или композициями) над М. Множество [М]наз. замыканием множества М. Задание конкретной модели М. л.
и наз. суперпозиция м и (или композициями) над М. Множество [М]наз. замыканием множества М. Задание конкретной модели М. л. считается эквивалентным указанию множеств Е, М,<M> и [М], при этом говорят, что модель порождается множеством М;если Мконечно, говорят, что модель является конечно порожденной. Эта модель наз. формульной моделью, а также т- значной логикой.
считается эквивалентным указанию множеств Е, М,<M> и [М], при этом говорят, что модель порождается множеством М;если Мконечно, говорят, что модель является конечно порожденной. Эта модель наз. формульной моделью, а также т- значной логикой. и бинарной операции
и бинарной операции 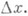 . В предположении, что каждая функция f из PE с учетом фиктивных переменных зависит от переменных х 1 , х 2, ... , х п, где попределяется функцией f, эти операции могут быть заданы так:
. В предположении, что каждая функция f из PE с учетом фиктивных переменных зависит от переменных х 1 , х 2, ... , х п, где попределяется функцией f, эти операции могут быть заданы так: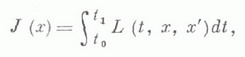
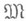 если n=1;
если n=1; 

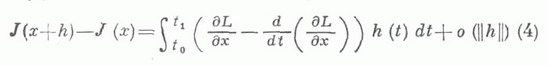
 иногда наз. алгебрами Поста.
иногда наз. алгебрами Поста.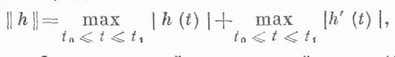 всех формул из
всех формул из 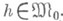 реализующих функции из
реализующих функции из  . Частным случаем такой задачи является важный вопрос математич. логики об указании всех формул, реализующих заданную константу, что, напр., для исчисления высказываний эквивалентно построению всех тождественно истинных высказываний.
. Частным случаем такой задачи является важный вопрос математич. логики об указании всех формул, реализующих заданную константу, что, напр., для исчисления высказываний эквивалентно построению всех тождественно истинных высказываний.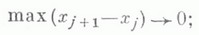 (тождеств), позволяющее путем подстановки выделенных равных формул одной вместо другой получить из любой формулы все формулы, равные ей (полную систему тождеств).
(тождеств), позволяющее путем подстановки выделенных равных формул одной вместо другой получить из любой формулы все формулы, равные ей (полную систему тождеств). заданного замкнутого, т. е. совпадающего со своим замыканием, множества М, для к-рых выполнено равенство
заданного замкнутого, т. е. совпадающего со своим замыканием, множества М, для к-рых выполнено равенство  т. е. имеет место свойство полноты (или свойство функциональной полноты) M1 в М. К этой задаче примыкает задача о базисах, состоящая в указании всех полных в Мподмножеств М 1 никакое собственное подмножество к-рых уже не полно в М(базисы называют также полными независимым и системами функций). Выделяют два подхода к решению задачи о полноте - алгоритмический и алгебраический. В первом случае ставится вопрос о существовании алгоритма, устанавливающего полноту или неполноту систем функций, описанных на нек-ром языке; во втором - переходят к изучению свойств решетки подалгебр данной алгебры m-значной логики и решают задачу о полноте, используя эти свойства. Важным понятием при алгебраич. подходе является понятие критериальной системы подалгебр. Система Nподалгебр алгебры
т. е. имеет место свойство полноты (или свойство функциональной полноты) M1 в М. К этой задаче примыкает задача о базисах, состоящая в указании всех полных в Мподмножеств М 1 никакое собственное подмножество к-рых уже не полно в М(базисы называют также полными независимым и системами функций). Выделяют два подхода к решению задачи о полноте - алгоритмический и алгебраический. В первом случае ставится вопрос о существовании алгоритма, устанавливающего полноту или неполноту систем функций, описанных на нек-ром языке; во втором - переходят к изучению свойств решетки подалгебр данной алгебры m-значной логики и решают задачу о полноте, используя эти свойства. Важным понятием при алгебраич. подходе является понятие критериальной системы подалгебр. Система Nподалгебр алгебры  наз. критериальной, если любое множество
наз. критериальной, если любое множество  является полным тогда и только тогда, когда оно не является подмножеством ни одной подалгебры из N. Таково, напр., множество всех собственных подалгебр алгебры М. В общем случае последняя критериальная система является избыточной. Всякая критериальная система содержит все максимальные подалгебры алгебры М(или предполные класс ы), и это позволяет перейти к рассмотрению более экономных критериальных систем, к-рые не содержат подалгебр максимальных подалгебр. Таким образом, в задачах о полноте можно ограничиться использованием критериальных систем вида
является полным тогда и только тогда, когда оно не является подмножеством ни одной подалгебры из N. Таково, напр., множество всех собственных подалгебр алгебры М. В общем случае последняя критериальная система является избыточной. Всякая критериальная система содержит все максимальные подалгебры алгебры М(или предполные класс ы), и это позволяет перейти к рассмотрению более экономных критериальных систем, к-рые не содержат подалгебр максимальных подалгебр. Таким образом, в задачах о полноте можно ограничиться использованием критериальных систем вида  где
где  - множество всех максимальных подалгебр, а множество
- множество всех максимальных подалгебр, а множество 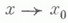 состоит из нек-рых таких подалгебр, к-рые не являются подалгебрами никакой максимальной подалгебры. В случае пустоты е 2 задача о полноте сводится к описанию максимальных подалгебр алгебры N.
состоит из нек-рых таких подалгебр, к-рые не являются подалгебрами никакой максимальной подалгебры. В случае пустоты е 2 задача о полноте сводится к описанию максимальных подалгебр алгебры N. существуют m-значные логики с конечным базисом и в то же время не имеющие конечной полной системы тождеств (см. [4]), тогда как в двузначной логике каждый замкнутый класс имеет конечную полную систему тождеств (см. [5]). Для конечнозначных логик с конечным базисом имеется эффективное решение задачи о полноте. Оно достигается следующим путем. Говорят, что функция f(x1,... , х п). сохраняет множество К= {g1(x1 , ..., xn),..., gs(x1,..., xn)}, если для любого набора gi1 gi2,..., gik , где
существуют m-значные логики с конечным базисом и в то же время не имеющие конечной полной системы тождеств (см. [4]), тогда как в двузначной логике каждый замкнутый класс имеет конечную полную систему тождеств (см. [5]). Для конечнозначных логик с конечным базисом имеется эффективное решение задачи о полноте. Оно достигается следующим путем. Говорят, что функция f(x1,... , х п). сохраняет множество К= {g1(x1 , ..., xn),..., gs(x1,..., xn)}, если для любого набора gi1 gi2,..., gik , где  , имеет место
, имеет место 
 . Множество Кназ. правильным, если селекторная функция
. Множество Кназ. правильным, если селекторная функция  содержится в Кпри всех
содержится в Кпри всех  и каждая функция из Ксохраняет К. Если М=[К], то в М выбирают все системы
и каждая функция из Ксохраняет К. Если М=[К], то в М выбирают все системы 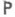 с такими свойствами: функции в них зависят только от
с такими свойствами: функции в них зависят только от  добавление к ним всех селекторных функций делает их правильными, они не содержат в качестве подмножества К. Указанная процедура выделения всех правильных множеств
добавление к ним всех селекторных функций делает их правильными, они не содержат в качестве подмножества К. Указанная процедура выделения всех правильных множеств 
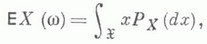 , является эффективной. Критериальной системой является
, является эффективной. Критериальной системой является 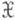 , где
, где 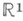 (класс сохранения К i )состоит из всех функций из М, сохраняющих
(класс сохранения К i )состоит из всех функций из М, сохраняющих 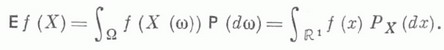 . Невключение произвольного конечного множества
. Невключение произвольного конечного множества  в каждый из классов
в каждый из классов  проверяется также эффективно. Каждый пред-полный класс является одним из классов сохранения, а множество всех предполных классов в этом случае образует критериальную систему. Показано, что при
проверяется также эффективно. Каждый пред-полный класс является одним из классов сохранения, а множество всех предполных классов в этом случае образует критериальную систему. Показано, что при 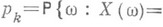 в
в 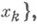 имеется континуум замкнутых классов, существуют замкнутые классы с базисами заданной конечной или счетной мощности, а также такие классы, к-рые не имеют базисов, при этом сами семейства классов без базисов или со счетным базисом континуальны. Примерами классов без базиса или имеющих счетный базис являются
имеется континуум замкнутых классов, существуют замкнутые классы с базисами заданной конечной или счетной мощности, а также такие классы, к-рые не имеют базисов, при этом сами семейства классов без базисов или со счетным базисом континуальны. Примерами классов без базиса или имеющих счетный базис являются  и
и 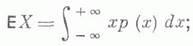
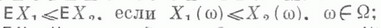 , где:
, где: 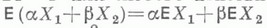 при n=0, а при n>0 функция fn( х 1 ,... , х п )равна 0 на всех наборах, кроме (2, ... , 2), на к-ром равна 1; gn(x1 , ..., х п ). равна 0 на всех наборах, кроме наборов вида (2, ... , 2,1, 2, ... , 2), на к-рых равна 1 (см. [6]).
при n=0, а при n>0 функция fn( х 1 ,... , х п )равна 0 на всех наборах, кроме (2, ... , 2), на к-ром равна 1; gn(x1 , ..., х п ). равна 0 на всех наборах, кроме наборов вида (2, ... , 2,1, 2, ... , 2), на к-рых равна 1 (см. [6]).
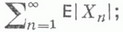 . Класс U(R)всех функций, сохраняющих предикат R, наз. классом сохранения предиката R. Показано, что для каждого предполного класса Nможно выбрать такой предикат R, зависящий не более чем от m+2 переменных, а при
. Класс U(R)всех функций, сохраняющих предикат R, наз. классом сохранения предиката R. Показано, что для каждого предполного класса Nможно выбрать такой предикат R, зависящий не более чем от m+2 переменных, а при 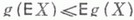 не более чем от тпеременных, что N= U(R). Эти предикаты могут быть разбиты на шесть семейств: Н. S, Е, L, Z, U. Семейства Н, S и Есостоят из всех двуместных предикатов отношения порядка на Е т, имеющих по одному максимальному и минимальному элементу,- в первом случае; задающих подстановки на Е т, разлагающиеся в циклы одинаковой простой длины (без инвариантных элементов),- во втором случае; и задающих нетождественные и неуниверсальные отношения эквивалентности на Е т- в третьем случае. Семейство Lне пусто при m=р h, р- простое, и состоит из всех четырехместных предикатов RG(y1 , у2, у 3 , y4 )таких, что RG (y1 , у2, у 3 , y4)=1 эквивалентно y1+ у2 = у 3 + y4., где G- абелева группа, в к-рой каждый ненулевой элемент имеет порядок р. Предикат R(y1 ,... у h ),
не более чем от тпеременных, что N= U(R). Эти предикаты могут быть разбиты на шесть семейств: Н. S, Е, L, Z, U. Семейства Н, S и Есостоят из всех двуместных предикатов отношения порядка на Е т, имеющих по одному максимальному и минимальному элементу,- в первом случае; задающих подстановки на Е т, разлагающиеся в циклы одинаковой простой длины (без инвариантных элементов),- во втором случае; и задающих нетождественные и неуниверсальные отношения эквивалентности на Е т- в третьем случае. Семейство Lне пусто при m=р h, р- простое, и состоит из всех четырехместных предикатов RG(y1 , у2, у 3 , y4 )таких, что RG (y1 , у2, у 3 , y4)=1 эквивалентно y1+ у2 = у 3 + y4., где G- абелева группа, в к-рой каждый ненулевой элемент имеет порядок р. Предикат R(y1 ,... у h ), 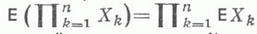 рефлексивен, если из того, что не все числа а 1 , а2, ... , ah различны, следует, что R(a1 , a2, ..., ah)=1, и симметричен, если для любой подстановки s чисел 1, 2, ... , hимеет место R(y1 ,... у h )= R(ys(1) , ... , ys(h)). Множество элементов
рефлексивен, если из того, что не все числа а 1 , а2, ... , ah различны, следует, что R(a1 , a2, ..., ah)=1, и симметричен, если для любой подстановки s чисел 1, 2, ... , hимеет место R(y1 ,... у h )= R(ys(1) , ... , ys(h)). Множество элементов  таких-то R(a1, ... , ah-1 , c)=1 для любых а 1 , ..., ah_1 , наз. центром симметричного предиката R. Предикат R(y1 ,... у h ) является центральным, если он рефлексивен, симметричен и имеет центр с такой, что
таких-то R(a1, ... , ah-1 , c)=1 для любых а 1 , ..., ah_1 , наз. центром симметричного предиката R. Предикат R(y1 ,... у h ) является центральным, если он рефлексивен, симметричен и имеет центр с такой, что  . Семейство 2состоит из всех h- местных центральных предикатов таких, что 1=<h=<m. Для аиз
. Семейство 2состоит из всех h- местных центральных предикатов таких, что 1=<h=<m. Для аиз  полагают
полагают 
 , для нек-рой сюръекции
, для нек-рой сюръекции  равенство R(a1, ... , ah) = l эквивалентно тому, что набор
равенство R(a1, ... , ah) = l эквивалентно тому, что набор  неразнозначен при любом l=0, 1, ... , k-1. Установлено, что предикаты из разных семейств задают разные предполные классы, и указаны условия, когда предикаты из одного и того же семейства задают одинаковые классы. Показано, что число предполных классов асимптотически равно
неразнозначен при любом l=0, 1, ... , k-1. Установлено, что предикаты из разных семейств задают разные предполные классы, и указаны условия, когда предикаты из одного и того же семейства задают одинаковые классы. Показано, что число предполных классов асимптотически равно  , где
, где  , если тчетно, и
, если тчетно, и  , если тнечетно (т. е. это число растет достаточно быстро), что указывает на малую практич. эффективность критериальных систем (см. [8]). Рассматриваются различные модификации задачи о полноте, сводящиеся к исследованию систем с нек-рыми заранее известными свойствами, напр, систем, содержащих множество
, если тнечетно (т. е. это число растет достаточно быстро), что указывает на малую практич. эффективность критериальных систем (см. [8]). Рассматриваются различные модификации задачи о полноте, сводящиеся к исследованию систем с нек-рыми заранее известными свойствами, напр, систем, содержащих множество  всех одноместных функций или же множество Sm всех подстановок. В первом случае система при m>2, а во втором при m>4 является полной тогда и только тогда, когда она содержит существенную функцию, т. <е. функцию, зависящую более чем от одного переменного и принимающую все тзначений (см. [9], [10]). С ними связана задача указания всех таких подмножеств Т множеств
всех одноместных функций или же множество Sm всех подстановок. В первом случае система при m>2, а во втором при m>4 является полной тогда и только тогда, когда она содержит существенную функцию, т. <е. функцию, зависящую более чем от одного переменного и принимающую все тзначений (см. [9], [10]). С ними связана задача указания всех таких подмножеств Т множеств  и
и  , каждое из к-рых вместе с любой существенной функцией образует полную систему. Показано, что подмножество
, каждое из к-рых вместе с любой существенной функцией образует полную систему. Показано, что подмножество  всех одноместных функций, не принимающих хотя бы одного значения, является таковым, а подмножество
всех одноместных функций, не принимающих хотя бы одного значения, является таковым, а подмножество  всех одноместных функций, не принимающих хотя бы двух значений, вообще говоря, таковым уже не является. При m>4 таковыми являются те и только те подмножества Т, к-рые 4-транзитивны при m=2k, 3-транзитивны при т=р к, р- простое,
всех одноместных функций, не принимающих хотя бы двух значений, вообще говоря, таковым уже не является. При m>4 таковыми являются те и только те подмножества Т, к-рые 4-транзитивны при m=2k, 3-транзитивны при т=р к, р- простое,  , 2-транзитивны при остальных т. Эти условия после естественного обобщения транзитивности сохраняются и для произвольных систем функций, к-рые принимают все тзначений (см. [11]).
, 2-транзитивны при остальных т. Эти условия после естественного обобщения транзитивности сохраняются и для произвольных систем функций, к-рые принимают все тзначений (см. [11]). -
- [12]. Число переменных у функций из простых базисов не превосходит
[12]. Число переменных у функций из простых базисов не превосходит  , и существует функция, входящая в простой базис и существенно зависящая от
, и существует функция, входящая в простой базис и существенно зависящая от  переменных. Указаны представления М. л. Pk в Р т, т. е. гомоморфизмы Р k в Р т[13]; построены также нек-рые аналоги теории минимизации для произвольных конечнозначных логик.
переменных. Указаны представления М. л. Pk в Р т, т. е. гомоморфизмы Р k в Р т[13]; построены также нек-рые аналоги теории минимизации для произвольных конечнозначных логик. всех одноместных функций [14]. В отличие от конечнозначных логик Р т при m>2, где имеется только один предполный класс, содержащий все одноместные функции, в
всех одноместных функций [14]. В отличие от конечнозначных логик Р т при m>2, где имеется только один предполный класс, содержащий все одноместные функции, в  существуют два таких предполных класса и указанная система функций является полной тогда и только тогда, когда она не содержится в этих классах. Если обобщить понятие существенной функции и считать, что таковой является всякая функция, образующая полную систему вместе с
существуют два таких предполных класса и указанная система функций является полной тогда и только тогда, когда она не содержится в этих классах. Если обобщить понятие существенной функции и считать, что таковой является всякая функция, образующая полную систему вместе с  , то так же, как и в конечнозначных логиках, возникает задача описания всех тех подмножеств множества
, то так же, как и в конечнозначных логиках, возникает задача описания всех тех подмножеств множества  , к-рые содержат все множество
, к-рые содержат все множество  подстановок из
подстановок из  н вместе с любой существенной функцией образуют полную систему. Показано, что пересечение всех таких замкнутых подмножеств само обладает указанным свойством. Это пересечение, к-рое отлично от
н вместе с любой существенной функцией образуют полную систему. Показано, что пересечение всех таких замкнутых подмножеств само обладает указанным свойством. Это пересечение, к-рое отлично от  эффективно описано в теоретико-множественных терминах.
эффективно описано в теоретико-множественных терминах. , содержащие гомоморфные прообразы всех конечнозначных логик. Существует континуум различных и даже конечно порожденных попарно неизоморфных предельных логик. Установлено, что в общем случае для предельных логик задача о полноте не эквивалентна отысканию всех предполных классов. Мощность множества предполных классов в предельных логиках может быть равной любому натуральному числу, а также быть счетной или континуальной (см. [15]). Для М. л. непрерывных функций показана полнота всех двуместных функций и получены нек-рые аналоги теоремы о полноте систем, состоящих из всех одноместных и многоместной функций. Установлено также, что всякую непрерывную функцию можно представить в виде суммы специально выбранных непрерывных одноместных функций. Показано, что для kраз дифференцируемых функций от ппеременных, вообще говоря, невозможно представление их с помощью суперпозиций функций той же гладкости, но зависящих от меньшего числа переменных (см. [16]).
, содержащие гомоморфные прообразы всех конечнозначных логик. Существует континуум различных и даже конечно порожденных попарно неизоморфных предельных логик. Установлено, что в общем случае для предельных логик задача о полноте не эквивалентна отысканию всех предполных классов. Мощность множества предполных классов в предельных логиках может быть равной любому натуральному числу, а также быть счетной или континуальной (см. [15]). Для М. л. непрерывных функций показана полнота всех двуместных функций и получены нек-рые аналоги теоремы о полноте систем, состоящих из всех одноместных и многоместной функций. Установлено также, что всякую непрерывную функцию можно представить в виде суммы специально выбранных непрерывных одноместных функций. Показано, что для kраз дифференцируемых функций от ппеременных, вообще говоря, невозможно представление их с помощью суперпозиций функций той же гладкости, но зависящих от меньшего числа переменных (см. [16]).