|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МНОГОГРАННИКА ГРУППАЗначение МНОГОГРАННИКА ГРУППА в математической энциклопедии: - группа Sym Рсимметрии многогранника Рв n-мерном евклидовом пространстве E n , т. е. группа всех движений пространства Е n, переводящих Рв себя. Многогранник Рназ. правильным, если группа Sym Pтранзитивно действует на множестве его "флагов" - наборов
где Группа симметрии правильного многогранника порождается отражениями (см. Отражений группа). Ее фундаментальной областью является симшшциальный конус К, вершина к-рого совпадает с центром многогранника Р, а ребра проходят через центры граней, составляющих какой-либо флаг F. Тем самым образующие отражения r1,..., r п группы Sym Pполучают естественную нумерацию: rk есть отражение относительно той гиперплоскости, ограничивающей K, к-рая не проходит через центр грани Г k-1. Образующие Символ Шлефли определяет правильный многогранник с точностью до подобия. Обращению символа Шлефли соответствует переход к взаимному многограннику, вершинами к-рого служат центры (п- 1)-мерных граней многогранника Р. Взаимные многогранники имеют одинаковые группы симметрии. Все возможные символы Шлефли правильных многогранников можно получить из классификации конечных групп отражений, выделив из них те, граф Кокстера к-рых линеен. При Каждая грань правильного многогранника Ртакже является правильным многогранником, причем ее символ Шлефли есть начальный отрезок символа Шлефли самого многогранника Р. Напр., 3-мерная грань многогранника {5, 3, 3} имеет символ Шлефли {5, 3}, т. е. является додекаэдром. Лит.:[1] Coxeter H. S. M., Regular Polytopes, 2 ed., N. Y.- L., 1963; [2] Pозенфельд Б. А., 'Многомерные пространства, М., 1066. Э. Б. Винберг. |
|
|
|


 есть k-мерная замкнутая грань и
есть k-мерная замкнутая грань и 
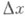 и
и 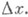 при
при  коммутируют, а порядок
коммутируют, а порядок 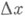 равен
равен  числу k-мерных (или (к-1)-мерных) граней многогранника Tk + 1 , содержащих грань
числу k-мерных (или (к-1)-мерных) граней многогранника Tk + 1 , содержащих грань  (если считать, что
(если считать, что  ). Последовательность
). Последовательность  наз. символом Шлефли многогранника. Трехмерные правильные многогранники (тела Платона) имеют следующие символы Шлефли: тетраэдр - {3,3}, куб - {4,3}, октаэдр - {3,4}, додекаэдр - {5,3}, икосаэдр - {3,5}.
наз. символом Шлефли многогранника. Трехмерные правильные многогранники (тела Платона) имеют следующие символы Шлефли: тетраэдр - {3,3}, куб - {4,3}, октаэдр - {3,4}, додекаэдр - {5,3}, икосаэдр - {3,5}.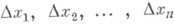 в
в  существует лишь 3 правильных многогранника: симплекс, куб и многогранник взаимный кубу (аналог октаэдра). Их символы Шлефли суть {3, ... , 3}, {4,3, ... , 3} и {3, ... , 3, 4}. В 4-мерном пространстве имеется 6 правильных многогранников; {3, 3, 3}, {4, 3, 3}, {3, 3, 4}, {3, 4, 3}, {5, 3, 3} и {3, 3, 5}.
существует лишь 3 правильных многогранника: симплекс, куб и многогранник взаимный кубу (аналог октаэдра). Их символы Шлефли суть {3, ... , 3}, {4,3, ... , 3} и {3, ... , 3, 4}. В 4-мерном пространстве имеется 6 правильных многогранников; {3, 3, 3}, {4, 3, 3}, {3, 3, 4}, {3, 4, 3}, {5, 3, 3} и {3, 3, 5}.