|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МИТТАГ-ЛЕФФЛЕРА ТЕОРЕМАЗначение МИТТАГ-ЛЕФФЛЕРА ТЕОРЕМА в математической энциклопедии: - 1) М.-Л. т. о разложении мероморфной функции (см. [1], [2]) - одна из основных теорем теории аналитических функций, дающая для мероморфных функций аналог разложения рациональной функции на простейшие дроби. Пусть
и
так что точка а n является единственным полюсом соответствующей функции gn(z). Тогда существуют мероморфные функции f(z)в плоскости С комплексного переменного z , имеющие полюсы в точках а п и только в них с заданными главными частями (1) Лорана рядов, соответствующих точкам а п. Все эти функции f(z)представимы в виде разложения Миттаг-Леффлера:
где pn(z)- нек-рые многочлены, подбираемые по а п и gn(z)так, чтобы ряд (2) равномерно (после выбрасывания конечного числа членов) сходился на любом компакте Из М.-Л. т. вытекает, что любая наперед заданная мероморфная функция f(z)в Справедливо обобщение приведенной теоремы, также принадлежащее Г. Миттаг-Леффлеру и состоящее в том, что каковы бы ни были область Dрасширенной комплексной плоскости Другое обобщение М.-Л. т. состоит в том, что для любых последовательности
являющихся целыми функциями относительно переменного Для аналитических функций многих комплексных переменных обобщением задачи Миттаг-Леффлера о построении функции с заданными особенностями является первая (аддитивная) Кузена проблема. В связи с этим часто оказывается полезной следующая равносильная формулировка М.-Л. т. Пусть 2) М.-Л. т. о разложении однозначной ветви аналитической функции в звезде - см. Звезда элемента функции. Лит.:[1] Мittag -Leffler G., En metod att analytisk framstalla en funktion at rationel karakter...- Ofversigt Kongl. Vetenskaps-Akad. Forhandlingar, 1876, v. 33, № 6, p. 3- 16; [2] eго жe, "Acta math.", 1884, v. 4, p. 1-79; [3] Гурcа Э., Курс математического анализа, пер. с франц., 3 изд., т. 2, М.-Л., 1936; [4] Маркушевич А. И., Теория аналитических функций, 2 изд., т. 2, М., 1968; [5] Шабат Б. В., Введение в комплексный анализ, 2 изд., ч. 1-2, М., 1976; [б] Хёрмандер Л., Введение в теорию функций нескольких комплексных переменных, пер. с англ., М., 1968; [7] Веhnke Н., Sommer P., Theorie der analytischen Funktionen einer komplexen Veranderlichen, 3 AufL, В., 1965; [8] Шварц Л., Анализ, пер. с франц., т. 2, М., 1972. Е. Д. Соломенцев. |
|
|
|

 - последовательность различных комплексных чисел
- последовательность различных комплексных чисел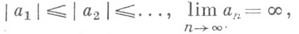
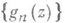 - последовательность рациональных функций вида
- последовательность рациональных функций вида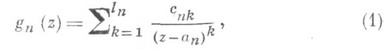
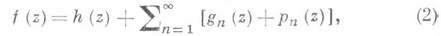
 - произвольная целая функция.
- произвольная целая функция.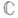 с полюсами аД и соответствующими главными частями gn(z)разложений f(z)в ряды Лорана в окрестности а а разлагается в ряд (2), где целая функция h(z)определяется по f(z). Г. Миттаг-Леффлер указал общую конструкцию многочленов pn{z), отыскание же целой функции h(z)по данной f(z) иногда представляет собой более трудную задачу. Для получения разложения (2) можно применить методы теории вычетов (см. также [3] - [5]).
с полюсами аД и соответствующими главными частями gn(z)разложений f(z)в ряды Лорана в окрестности а а разлагается в ряд (2), где целая функция h(z)определяется по f(z). Г. Миттаг-Леффлер указал общую конструкцию многочленов pn{z), отыскание же целой функции h(z)по данной f(z) иногда представляет собой более трудную задачу. Для получения разложения (2) можно применить методы теории вычетов (см. также [3] - [5]).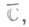 последовательность
последовательность 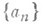 точек
точек 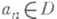 , все предельные точки к-рой находятся на границе
, все предельные точки к-рой находятся на границе 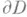 , и соответствующие главные части (1), существует мероморфная в Dфункция f(z), имеющая полюсы в точках а п и только в них с заданными главными частями (1). В такой форме М.-Л. т. обобщается и для открытых римановых поверхностен D(см. [7]); о существовании мероморфных функций с заданными особенностями на компактных римановых поверхностях см. Абелев дифференциал, Дифференциал на римановой поверхности, Римана- Роха теорема. М.-Л. т. верна и для абстрактных мероморфных функций
, и соответствующие главные части (1), существует мероморфная в Dфункция f(z), имеющая полюсы в точках а п и только в них с заданными главными частями (1). В такой форме М.-Л. т. обобщается и для открытых римановых поверхностен D(см. [7]); о существовании мероморфных функций с заданными особенностями на компактных римановых поверхностях см. Абелев дифференциал, Дифференциал на римановой поверхности, Римана- Роха теорема. М.-Л. т. верна и для абстрактных мероморфных функций 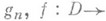
 со значениями в банаховом пространстве F(см. [8]).
со значениями в банаховом пространстве F(см. [8]).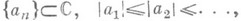
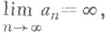 и соответствующих функций
и соответствующих функций
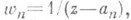 существует однозначная аналитическая функция f(z), имеющая особые точки а п и только их с главными частями gn(z)(см. [3]).
существует однозначная аналитическая функция f(z), имеющая особые точки а п и только их с главными частями gn(z)(см. [3]). где
где 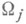 - открытые множества в
- открытые множества в  , и пусть даны мероморфные функции
, и пусть даны мероморфные функции 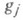 соответственно на множествах
соответственно на множествах 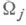 , причем разности
, причем разности  суть регулярные функции на пересечениях
суть регулярные функции на пересечениях  при всех j и k. Тогда на Qсуществует мероморфная функция f такая, что разности f-gj регулярны на
при всех j и k. Тогда на Qсуществует мероморфная функция f такая, что разности f-gj регулярны на 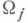 для всех j (см. [5], [6]).
для всех j (см. [5], [6]).