"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МИНИМИЗАЦИЯ ВЫЧИСЛИТЕЛЬНОЙ РАБОТЫ
Значение МИНИМИЗАЦИЯ ВЫЧИСЛИТЕЛЬНОЙ РАБОТЫ в математической энциклопедии:
- раздел современной вычислительной математики, посвященный конструированию и исследованию методов, позволяющих находить приближенное с заранее указываемой точностью  решение поставленной задачи Риз класса {Р}при наименьших затратах вычислительной работы (при наименьшем объеме вычислений). Этот раздел вычислительной математики может быть отнесен к более общему, имеющему дело с задачей оптимизации методов (см., напр., [1], [2]), в к-ром наряду с указанной проблемой М. в. р. рассматривается и двойственная по отношению к ней проблема нахождения среди приближенных методов, требующих примерно одинаковой допустимой вычислительной работы, метода, обладающего максимальной точностью (наименьшей погрешностью). Последняя проблема характерна, напр., для задач численного интегрирования, в к-рых фиксируется число узлов интегрирования, служащее мерой совершаемой вычислительной работы. Пусть
решение поставленной задачи Риз класса {Р}при наименьших затратах вычислительной работы (при наименьшем объеме вычислений). Этот раздел вычислительной математики может быть отнесен к более общему, имеющему дело с задачей оптимизации методов (см., напр., [1], [2]), в к-ром наряду с указанной проблемой М. в. р. рассматривается и двойственная по отношению к ней проблема нахождения среди приближенных методов, требующих примерно одинаковой допустимой вычислительной работы, метода, обладающего максимальной точностью (наименьшей погрешностью). Последняя проблема характерна, напр., для задач численного интегрирования, в к-рых фиксируется число узлов интегрирования, служащее мерой совершаемой вычислительной работы. Пусть  (обычно
(обычно  при
при  ищется точное решение Р)- требуемая точность решения задачи Риз заданного класса
ищется точное решение Р)- требуемая точность решения задачи Риз заданного класса  родственных задач, a m - допустимый метод для отыскания решения любой задачи из
родственных задач, a m - допустимый метод для отыскания решения любой задачи из  , и множество таких методов обозначено через
, и множество таких методов обозначено через  . Пусть число
. Пусть число  характеризует затраты вычислительной работы в методе т, позволяющие найти решение Рс точностью
характеризует затраты вычислительной работы в методе т, позволяющие найти решение Рс точностью  , а
, а

Тогда задача минимизации состоит в отыскании такого метода т 0, что

то есть по существу ищется оптимальный метод решения не одной фиксированной задачи Р, а целого класса задач (оптимизация на классе). Чаще же всего М. в. р. производится в асимптотич. смысле при  где N - параметр, определяющий "размерность" решаемой задачи.
где N - параметр, определяющий "размерность" решаемой задачи.
Метод  наз. оптимальным по порядку, если затраты вычислительной работы в нем не превышают более чем в конечное число раз величину
наз. оптимальным по порядку, если затраты вычислительной работы в нем не превышают более чем в конечное число раз величину  - полученных оценок снизу затрат вычислительной работы в любом возможном методе; метод т 0 наз. логарифмически оптимальным, если
- полученных оценок снизу затрат вычислительной работы в любом возможном методе; метод т 0 наз. логарифмически оптимальным, если

Вычислительная же работа  обычно характеризуется числом арифметич. действий, производимых в методе тдля достижения точности е пря его реализации на условной ЭВМ. До какой-то степени это является оправданным упрощением, поскольку во многих методах логич. операций на реальных ЭВМ совершается лишь в конечное число раз больше, чем арифметических. От допустимых методов, как правило, требуют их устойчивости по отношению к ошибкам округления. Важно, чтобы и асимптотич. рост количества используемых ячеек машинной памяти не был в этих методах чересчур большим.
обычно характеризуется числом арифметич. действий, производимых в методе тдля достижения точности е пря его реализации на условной ЭВМ. До какой-то степени это является оправданным упрощением, поскольку во многих методах логич. операций на реальных ЭВМ совершается лишь в конечное число раз больше, чем арифметических. От допустимых методов, как правило, требуют их устойчивости по отношению к ошибкам округления. Важно, чтобы и асимптотич. рост количества используемых ячеек машинной памяти не был в этих методах чересчур большим.
При конкретизации указанных задач М. в. р. должно быть уточнено и описание класса  и указано метрич. пространство H, с помощью к-рого определяется точность решения исходной задачи.
и указано метрич. пространство H, с помощью к-рого определяется точность решения исходной задачи.
Решение многих таких конкретных проблем минимизации представляет не только теоретич. интерес, но и имеет большое прикладное значение, позволяя часто решать задачи на ЭВМ при сравнительно небольших затратах машинного времени. Особенно это важно пли для задач, требующих большого объема вычислений, что характерно, напр., для многомерных задач мате-матич. физики (см. [2] - [10]), или для задач, подобных задачам вычисления элементарных функций и нахождения дискретных преобразований Фурье (см. [1], [11]), являющихся стандартными, и многократно используемых для решения других, более сложных. Указанные задачи М. в. р. достаточно сложны и во многих случаях их решения получены лишь частично или даже пока (1982) совсем не известны.
На практике при решении задач не очень большой размерности и не с очень большой точностью иногда метод с худшими асимптотич. характеристиками может потребовать меньше машинного времени. Часто же если затраты вычислительной работы приемлемы, то руководствуются при выборе метода прежде всего соображениями его простоты и надежности.
Пусть исходная задача конечномерна и существуют методы, дающие точное решение за конечное число арифметич. действий, если эти действия совершаются без ошибок округления. В качестве примеров можно взять задачу вычисления значения многочлена  степени Nпри заданном значении хс
степени Nпри заданном значении хс  , перемножения двух квадратных матриц порядка N, решения определенной системы линейных алгебраич. уравнений
, перемножения двух квадратных матриц порядка N, решения определенной системы линейных алгебраич. уравнений 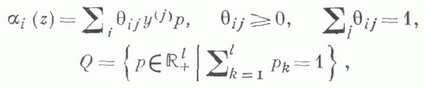 с квадратной матрицей порядка N и задачу нахождения дискретного преобразования Фурье (см. [1], [11]):
с квадратной матрицей порядка N и задачу нахождения дискретного преобразования Фурье (см. [1], [11]):

где i - мнимая единица, вектор  задан и ищется вектор
задан и ищется вектор 
 Никаких конкретных ограничений на вид
Никаких конкретных ограничений на вид  число
число  и вектор ине накладывается, и поэтому в каждой из этих задач допустимый класс
и вектор ине накладывается, и поэтому в каждой из этих задач допустимый класс  состоит из всех задач такого вида. В подобных задачах Nвыступает в роли параметра и особое внимание уделяется поведению затрат вычислительной работы
состоит из всех задач такого вида. В подобных задачах Nвыступает в роли параметра и особое внимание уделяется поведению затрат вычислительной работы  при
при  . Для первой из этих задач метод Горнера, записывающий
. Для первой из этих задач метод Горнера, записывающий 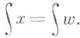 в виде
в виде

позволяет вычислить  за Nумножений и Nсложений. Доказано (см. [11]), что этот метод является оптимальным; не существует метода, к-рый требовал бы меньшего суммарного числа сложений и вычитаний или меньшего числа умножений и делений; устойчивость его приемлема, если
за Nумножений и Nсложений. Доказано (см. [11]), что этот метод является оптимальным; не существует метода, к-рый требовал бы меньшего суммарного числа сложений и вычитаний или меньшего числа умножений и делений; устойчивость его приемлема, если  не велика (см. [1]).
не велика (см. [1]).
Для второй и третьей задач существует большое число методов, дающих их решения при  за
за  арифметич. действий (см. [1]) и реально применяемых на практике. Наименьшие же затраты вычислительной работы среди всех пока известных методов достигаются на методе с оценкой
арифметич. действий (см. [1]) и реально применяемых на практике. Наименьшие же затраты вычислительной работы среди всех пока известных методов достигаются на методе с оценкой  (см. [11]). Этот метод достаточно сложен и по ряду причин интересен пока только с теоретич. точки зрения. Не известно (1982), является ли он даже логарифмически оптимальным. Имеется гипотеза, что у логарифмически оптимального метода с числом арифметич. действий W(N) должно быть
(см. [11]). Этот метод достаточно сложен и по ряду причин интересен пока только с теоретич. точки зрения. Не известно (1982), является ли он даже логарифмически оптимальным. Имеется гипотеза, что у логарифмически оптимального метода с числом арифметич. действий W(N) должно быть 
Для задачи же (1), являющейся предметом гармонич. анализа, простейшие методы требуют  арифметич.
арифметич.
действий с комплексными числами. В 1965 был предложен метод, позволяющий находить вектор за 
 арифметич. действий (см. [1], [11]), получивший название метода быстрого дискретного преобразования Фурье. Этот метод является логарифмически оптимальным; он широко применяется и на практике. Имеется большое число подобных задач минимизации, решенных и нерешенных (см. [11], [12]); оптимальные по порядку или логарифмически оптимальные оценки затрат вычислительной работы для нахождения решения подобных задач могут рассматриваться как показатель их сложности. М. в. р. при решении сеточных систем уравнений, возникающих или в разностных методах, или в проек-ционно-разностных (методах конечных элементов) для приближенного решения краевых задач для уравнений и систем уравнений сильно эллиптич. типа, имеет особое теоретическое и прикладное значение и обычно осуществляется асимптотически при
арифметич. действий (см. [1], [11]), получивший название метода быстрого дискретного преобразования Фурье. Этот метод является логарифмически оптимальным; он широко применяется и на практике. Имеется большое число подобных задач минимизации, решенных и нерешенных (см. [11], [12]); оптимальные по порядку или логарифмически оптимальные оценки затрат вычислительной работы для нахождения решения подобных задач могут рассматриваться как показатель их сложности. М. в. р. при решении сеточных систем уравнений, возникающих или в разностных методах, или в проек-ционно-разностных (методах конечных элементов) для приближенного решения краевых задач для уравнений и систем уравнений сильно эллиптич. типа, имеет особое теоретическое и прикладное значение и обычно осуществляется асимптотически при  , где N - число неизвестных в системе, и при
, где N - число неизвестных в системе, и при  . Для решения простейших разностных аналогов нек-рых краевых задач для уравнения Пуассона в прямоугольнике или параллелепипеде успешно применяются нек-рые прямые методы, являющиеся логарифмически оптимальными и требующие затраты
. Для решения простейших разностных аналогов нек-рых краевых задач для уравнения Пуассона в прямоугольнике или параллелепипеде успешно применяются нек-рые прямые методы, являющиеся логарифмически оптимальными и требующие затраты  арифметич. действий (см. [3], [5], [13], [14]). Известен в случае прямоугольника (см. [15]) и оптимальный по порядку метод, требующий O(N)действий. Используя же итерационные методы, удается получить логарифмически оптимальные оценки типа
арифметич. действий (см. [3], [5], [13], [14]). Известен в случае прямоугольника (см. [15]) и оптимальный по порядку метод, требующий O(N)действий. Используя же итерационные методы, удается получить логарифмически оптимальные оценки типа

где  - точность решения системы в той или иной метрике, для довольно широкого класса дискретных краевых задач на параллелепипедной сетке для линейных и нелинейных сильно эллиптич. систем, рассматриваемых в нек-рых идеальных областях (см. [2] - [10], [16], [17]) (напр., на плоскости Qможет быть образована из конечного числа прямоугольников со сторонами, параллельными осям координат, а в случае трехмерного пространства Qдолжна конечным числом плоских разрезов, параллельных заданной координатной плоскости, разбиваться на параллелепипеды с гранями, параллельными координатным плоскостям). Для более сложных областей
- точность решения системы в той или иной метрике, для довольно широкого класса дискретных краевых задач на параллелепипедной сетке для линейных и нелинейных сильно эллиптич. систем, рассматриваемых в нек-рых идеальных областях (см. [2] - [10], [16], [17]) (напр., на плоскости Qможет быть образована из конечного числа прямоугольников со сторонами, параллельными осям координат, а в случае трехмерного пространства Qдолжна конечным числом плоских разрезов, параллельных заданной координатной плоскости, разбиваться на параллелепипеды с гранями, параллельными координатным плоскостям). Для более сложных областей  использование сеток, топологически эквивалентных указанным сеткам идеальных областей Q, и нек-рых типов проекционно-разностных методов позволяет часто получить системы уравнений, решаемые столь же эффективно, что и в случае идеальных областей (см. [3], [8], [10], [16], [17]). При этом правые части этих систем могли быть любыми векторами; если же учитывать, что они порождались специальным образом как нек-рые функционалы от достаточно гладких функций, то удается построить методы с затратами работы О (NInN)и даже O(N)при условии, что
использование сеток, топологически эквивалентных указанным сеткам идеальных областей Q, и нек-рых типов проекционно-разностных методов позволяет часто получить системы уравнений, решаемые столь же эффективно, что и в случае идеальных областей (см. [3], [8], [10], [16], [17]). При этом правые части этих систем могли быть любыми векторами; если же учитывать, что они порождались специальным образом как нек-рые функционалы от достаточно гладких функций, то удается построить методы с затратами работы О (NInN)и даже O(N)при условии, что  Методы последнего типа для решения задачи на заданной сетке используют последовательность подобных же задач на более редких сетках.
Методы последнего типа для решения задачи на заданной сетке используют последовательность подобных же задач на более редких сетках.
Существуют методы, позволяющие найти с точностью  младшие собственное значение и соответствующую собственную функцию для нек-рых сеточных аналогов эллиптич. задач на собственные значения, при затрате
младшие собственное значение и соответствующую собственную функцию для нек-рых сеточных аналогов эллиптич. задач на собственные значения, при затрате  или даже
или даже  (при
(при 
 ) действий (см. [9]). Пусть задача Рсостоит в решении корректного операторного уравнения
) действий (см. [9]). Пусть задача Рсостоит в решении корректного операторного уравнения

оператор Lдействует из Нв F, где Ни F- бесконечномерные банаховы пространства. Пусть класс  состоит из таких задач с различными f, при к-рых решения уравнения (2) принадлежат нек-рому компакту U. Обычно Uзадается условием:
состоит из таких задач с различными f, при к-рых решения уравнения (2) принадлежат нек-рому компакту U. Обычно Uзадается условием:

где  - нек-рое банахово пространство, вложенное в Н. Если
- нек-рое банахово пространство, вложенное в Н. Если  ищется с точностью
ищется с точностью  в норме Н, то часто известны информационные оценки, равномерные относительно всех
в норме Н, то часто известны информационные оценки, равномерные относительно всех  наименьшей размерности
наименьшей размерности  вектора
вектора  задание к-рого позволяет получить элемент
задание к-рого позволяет получить элемент

(см. [1], [2], [6], [7], [18], [19]). Эти оценки снизу для N(e)дают и очевидные оценки снизу для необходимых затрат вычислительной работы в любом допустимом методе. Для ряда краевых задач сильно эллиптич. систем построены варианты проекционно-разностных методов, приводящих к алгебраич. системам уравнений

с Nнеизвестными, для к-рых, во-первых, известны оптимальные по порядку итерационные методы приближенного решения и, во-вторых, соответствующие восполнения  вектора
вектора  (см. [4]) являются
(см. [4]) являются  -аппроксимациями в Нрешения уравнения (2), причем
-аппроксимациями в Нрешения уравнения (2), причем  , где k- константа, не зависящая от
, где k- константа, не зависящая от  (см. [6] - [8], [10], [17]). Если не учитывать работу на формирование (5), то такие методы приводят к оценкам затраты вычислительной работы, минимальным по порядку. Напр., для случая эллиптич. уравнения 2-го порядка
(см. [6] - [8], [10], [17]). Если не учитывать работу на формирование (5), то такие методы приводят к оценкам затраты вычислительной работы, минимальным по порядку. Напр., для случая эллиптич. уравнения 2-го порядка  - пространство С. Л. Соболева [20]), если
- пространство С. Л. Соболева [20]), если  - область на плоскости, достижимы оценки затрат числа арифметич. действий
- область на плоскости, достижимы оценки затрат числа арифметич. действий  Вычислительную работу на формирование (5) тоже часто можно оценить как
Вычислительную работу на формирование (5) тоже часто можно оценить как  , если брать информацию о заданных функциях в соответствующих пространствах. В частности, в упомянутом примере f должна рассматриваться как элемент
, если брать информацию о заданных функциях в соответствующих пространствах. В частности, в упомянутом примере f должна рассматриваться как элемент  , но не
, но не  (см. [8], [17]). Подобного рода оценки получены и для нек-рых дифференциальных задач на собственные значения (см. [9]).
(см. [8], [17]). Подобного рода оценки получены и для нек-рых дифференциальных задач на собственные значения (см. [9]).
Рассматривались нек-рые вопросы М. в. р. при рeшении интегральных уравнений, обыкновенных дифференциальных уравнений и нестационарных уравнений с частными производными (см., напр., [1] - [4], [21] - [23]).
Лит.:[1] Бахвалов Н. С, Численные методы, 2 изд., М., 1975; [2] его же, в сб.: Международный конгресс математиков в Ницце, 1970, М., 1972, с. 27-33; [3] Марчук Г. И., Методы вычислительной математики, М., 1977; [4] Самарский А. А., Введение в теорию разностных схем, М., 1971; [5] Самарский А. А., Николаев B.C., Методы решения сеточных уравнений, М., 1978; [6] Оганесян Л. А., Ривкинд В. Я., Руховец Л. А., в сб.: Дифференциальные уравнения и их применения, Вильнюс, в. 5, 1973; в. 8, 1974; [7] Дьяконов Е. <Г., "Численные методы механики сплошной среды", Новосиб., 1976, т. 7, № 5, с. 14-78; [8] его же, в кн.: Вариационно-разностные методы в математической физике, Новосиб., 1978; с. 149-64; [9] Дьяконов Е. Г., Орехов М. Ю., "Матем. заметки", 1980, т. 27, № 5; [10] Корнеев В. Г., Схемы метода конечных элементов высоких порядков точности, Л., 1977; [11] Borodin A., Munio I., The Computational Complexity of Algebraic and Numeric Problems, N. Y., 1975; [12] Analytic Computational Complexity, N. Y., 1976; [13] Concus P., Golub G., "SIAM J. Numer. Anal.", 1973, v. 10, p. 1103-20; [14] Barker R. J., в кн.: Mathematical models and numerical methods (Banach Center Publications), Warsz., 1978, v. 3, p. 255-68; [15] Bank R.K., Rose D. J., "Proc. Symp. Carnegie-Mellon Univ.", N. Y., 1976, p. 201-49; [16] Кузнецов Ю. А., в кн.: Вариационно-разностные методы в математической физике, Новосиб., 1978, с. 178-212; [17] Дьяконов Е. Г., в кн.: Численные методы в математической физике, Новосиб., 1979, с. 45-68; [18] Теоретические основы и конструирование численных алгоритмов задач математической физики, М., 1979, с. 45-118; [19] Тихомиров В. М., Некоторые вопросы теории приближений, М., 1976; [20] Соболев С. Л., Некоторые применения функционального анализа в математической физике, Новосиб., 1962; [21] Емельянов К. В., ИльинА. М., "Ж. вычисл. матем. и матем. физ.", 1967, т. 7, № 4, с. 905-10; [22] Иванов В. В., в кн.: Механика сплошной среды и родственные проблемы анализа, М., 1972, с. 209-19; [23] Акопян Ю. Р., Оганесян Л. А., "Ж. вычисл. матем. и матем. физ.", 1977, т. 17, № 1, с. 109 - 18.
Е. Г. Дьяконов.

 решение поставленной задачи Риз класса {Р}при наименьших затратах вычислительной работы (при наименьшем объеме вычислений). Этот раздел вычислительной математики может быть отнесен к более общему, имеющему дело с задачей оптимизации методов (см., напр., [1], [2]), в к-ром наряду с указанной проблемой М. в. р. рассматривается и двойственная по отношению к ней проблема нахождения среди приближенных методов, требующих примерно одинаковой допустимой вычислительной работы, метода, обладающего максимальной точностью (наименьшей погрешностью). Последняя проблема характерна, напр., для задач численного интегрирования, в к-рых фиксируется число узлов интегрирования, служащее мерой совершаемой вычислительной работы. Пусть
решение поставленной задачи Риз класса {Р}при наименьших затратах вычислительной работы (при наименьшем объеме вычислений). Этот раздел вычислительной математики может быть отнесен к более общему, имеющему дело с задачей оптимизации методов (см., напр., [1], [2]), в к-ром наряду с указанной проблемой М. в. р. рассматривается и двойственная по отношению к ней проблема нахождения среди приближенных методов, требующих примерно одинаковой допустимой вычислительной работы, метода, обладающего максимальной точностью (наименьшей погрешностью). Последняя проблема характерна, напр., для задач численного интегрирования, в к-рых фиксируется число узлов интегрирования, служащее мерой совершаемой вычислительной работы. Пусть  (обычно
(обычно  при
при  ищется точное решение Р)- требуемая точность решения задачи Риз заданного класса
ищется точное решение Р)- требуемая точность решения задачи Риз заданного класса  родственных задач, a m - допустимый метод для отыскания решения любой задачи из
родственных задач, a m - допустимый метод для отыскания решения любой задачи из  , и множество таких методов обозначено через
, и множество таких методов обозначено через  . Пусть число
. Пусть число  характеризует затраты вычислительной работы в методе т, позволяющие найти решение Рс точностью
характеризует затраты вычислительной работы в методе т, позволяющие найти решение Рс точностью  , а
, а

 где N - параметр, определяющий "размерность" решаемой задачи.
где N - параметр, определяющий "размерность" решаемой задачи. наз. оптимальным по порядку, если затраты вычислительной работы в нем не превышают более чем в конечное число раз величину
наз. оптимальным по порядку, если затраты вычислительной работы в нем не превышают более чем в конечное число раз величину  - полученных оценок снизу затрат вычислительной работы в любом возможном методе; метод т 0 наз. логарифмически оптимальным, если
- полученных оценок снизу затрат вычислительной работы в любом возможном методе; метод т 0 наз. логарифмически оптимальным, если
 обычно характеризуется числом арифметич. действий, производимых в методе тдля достижения точности е пря его реализации на условной ЭВМ. До какой-то степени это является оправданным упрощением, поскольку во многих методах логич. операций на реальных ЭВМ совершается лишь в конечное число раз больше, чем арифметических. От допустимых методов, как правило, требуют их устойчивости по отношению к ошибкам округления. Важно, чтобы и асимптотич. рост количества используемых ячеек машинной памяти не был в этих методах чересчур большим.
обычно характеризуется числом арифметич. действий, производимых в методе тдля достижения точности е пря его реализации на условной ЭВМ. До какой-то степени это является оправданным упрощением, поскольку во многих методах логич. операций на реальных ЭВМ совершается лишь в конечное число раз больше, чем арифметических. От допустимых методов, как правило, требуют их устойчивости по отношению к ошибкам округления. Важно, чтобы и асимптотич. рост количества используемых ячеек машинной памяти не был в этих методах чересчур большим. и указано метрич. пространство H, с помощью к-рого определяется точность решения исходной задачи.
и указано метрич. пространство H, с помощью к-рого определяется точность решения исходной задачи. степени Nпри заданном значении хс
степени Nпри заданном значении хс  , перемножения двух квадратных матриц порядка N, решения определенной системы линейных алгебраич. уравнений
, перемножения двух квадратных матриц порядка N, решения определенной системы линейных алгебраич. уравнений 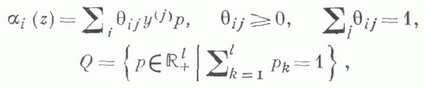 с квадратной матрицей порядка N и задачу нахождения дискретного преобразования Фурье (см. [1], [11]):
с квадратной матрицей порядка N и задачу нахождения дискретного преобразования Фурье (см. [1], [11]):
 задан и ищется вектор
задан и ищется вектор 
 Никаких конкретных ограничений на вид
Никаких конкретных ограничений на вид  число
число  и вектор ине накладывается, и поэтому в каждой из этих задач допустимый класс
и вектор ине накладывается, и поэтому в каждой из этих задач допустимый класс  состоит из всех задач такого вида. В подобных задачах Nвыступает в роли параметра и особое внимание уделяется поведению затрат вычислительной работы
состоит из всех задач такого вида. В подобных задачах Nвыступает в роли параметра и особое внимание уделяется поведению затрат вычислительной работы  при
при  . Для первой из этих задач метод Горнера, записывающий
. Для первой из этих задач метод Горнера, записывающий 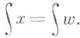 в виде
в виде
 за Nумножений и Nсложений. Доказано (см. [11]), что этот метод является оптимальным; не существует метода, к-рый требовал бы меньшего суммарного числа сложений и вычитаний или меньшего числа умножений и делений; устойчивость его приемлема, если
за Nумножений и Nсложений. Доказано (см. [11]), что этот метод является оптимальным; не существует метода, к-рый требовал бы меньшего суммарного числа сложений и вычитаний или меньшего числа умножений и делений; устойчивость его приемлема, если  не велика (см. [1]).
не велика (см. [1]). за
за  арифметич. действий (см. [1]) и реально применяемых на практике. Наименьшие же затраты вычислительной работы среди всех пока известных методов достигаются на методе с оценкой
арифметич. действий (см. [1]) и реально применяемых на практике. Наименьшие же затраты вычислительной работы среди всех пока известных методов достигаются на методе с оценкой  (см. [11]). Этот метод достаточно сложен и по ряду причин интересен пока только с теоретич. точки зрения. Не известно (1982), является ли он даже логарифмически оптимальным. Имеется гипотеза, что у логарифмически оптимального метода с числом арифметич. действий W(N) должно быть
(см. [11]). Этот метод достаточно сложен и по ряду причин интересен пока только с теоретич. точки зрения. Не известно (1982), является ли он даже логарифмически оптимальным. Имеется гипотеза, что у логарифмически оптимального метода с числом арифметич. действий W(N) должно быть 
 арифметич.
арифметич.
 арифметич. действий (см. [1], [11]), получивший название метода быстрого дискретного преобразования Фурье. Этот метод является логарифмически оптимальным; он широко применяется и на практике. Имеется большое число подобных задач минимизации, решенных и нерешенных (см. [11], [12]); оптимальные по порядку или логарифмически оптимальные оценки затрат вычислительной работы для нахождения решения подобных задач могут рассматриваться как показатель их сложности. М. в. р. при решении сеточных систем уравнений, возникающих или в разностных методах, или в проек-ционно-разностных (методах конечных элементов) для приближенного решения краевых задач для уравнений и систем уравнений сильно эллиптич. типа, имеет особое теоретическое и прикладное значение и обычно осуществляется асимптотически при
арифметич. действий (см. [1], [11]), получивший название метода быстрого дискретного преобразования Фурье. Этот метод является логарифмически оптимальным; он широко применяется и на практике. Имеется большое число подобных задач минимизации, решенных и нерешенных (см. [11], [12]); оптимальные по порядку или логарифмически оптимальные оценки затрат вычислительной работы для нахождения решения подобных задач могут рассматриваться как показатель их сложности. М. в. р. при решении сеточных систем уравнений, возникающих или в разностных методах, или в проек-ционно-разностных (методах конечных элементов) для приближенного решения краевых задач для уравнений и систем уравнений сильно эллиптич. типа, имеет особое теоретическое и прикладное значение и обычно осуществляется асимптотически при  , где N - число неизвестных в системе, и при
, где N - число неизвестных в системе, и при  . Для решения простейших разностных аналогов нек-рых краевых задач для уравнения Пуассона в прямоугольнике или параллелепипеде успешно применяются нек-рые прямые методы, являющиеся логарифмически оптимальными и требующие затраты
. Для решения простейших разностных аналогов нек-рых краевых задач для уравнения Пуассона в прямоугольнике или параллелепипеде успешно применяются нек-рые прямые методы, являющиеся логарифмически оптимальными и требующие затраты  арифметич. действий (см. [3], [5], [13], [14]). Известен в случае прямоугольника (см. [15]) и оптимальный по порядку метод, требующий O(N)действий. Используя же итерационные методы, удается получить логарифмически оптимальные оценки типа
арифметич. действий (см. [3], [5], [13], [14]). Известен в случае прямоугольника (см. [15]) и оптимальный по порядку метод, требующий O(N)действий. Используя же итерационные методы, удается получить логарифмически оптимальные оценки типа
 - точность решения системы в той или иной метрике, для довольно широкого класса дискретных краевых задач на параллелепипедной сетке для линейных и нелинейных сильно эллиптич. систем, рассматриваемых в нек-рых идеальных областях (см. [2] - [10], [16], [17]) (напр., на плоскости Qможет быть образована из конечного числа прямоугольников со сторонами, параллельными осям координат, а в случае трехмерного пространства Qдолжна конечным числом плоских разрезов, параллельных заданной координатной плоскости, разбиваться на параллелепипеды с гранями, параллельными координатным плоскостям). Для более сложных областей
- точность решения системы в той или иной метрике, для довольно широкого класса дискретных краевых задач на параллелепипедной сетке для линейных и нелинейных сильно эллиптич. систем, рассматриваемых в нек-рых идеальных областях (см. [2] - [10], [16], [17]) (напр., на плоскости Qможет быть образована из конечного числа прямоугольников со сторонами, параллельными осям координат, а в случае трехмерного пространства Qдолжна конечным числом плоских разрезов, параллельных заданной координатной плоскости, разбиваться на параллелепипеды с гранями, параллельными координатным плоскостям). Для более сложных областей  использование сеток, топологически эквивалентных указанным сеткам идеальных областей Q, и нек-рых типов проекционно-разностных методов позволяет часто получить системы уравнений, решаемые столь же эффективно, что и в случае идеальных областей (см. [3], [8], [10], [16], [17]). При этом правые части этих систем могли быть любыми векторами; если же учитывать, что они порождались специальным образом как нек-рые функционалы от достаточно гладких функций, то удается построить методы с затратами работы О (NInN)и даже O(N)при условии, что
использование сеток, топологически эквивалентных указанным сеткам идеальных областей Q, и нек-рых типов проекционно-разностных методов позволяет часто получить системы уравнений, решаемые столь же эффективно, что и в случае идеальных областей (см. [3], [8], [10], [16], [17]). При этом правые части этих систем могли быть любыми векторами; если же учитывать, что они порождались специальным образом как нек-рые функционалы от достаточно гладких функций, то удается построить методы с затратами работы О (NInN)и даже O(N)при условии, что  Методы последнего типа для решения задачи на заданной сетке используют последовательность подобных же задач на более редких сетках.
Методы последнего типа для решения задачи на заданной сетке используют последовательность подобных же задач на более редких сетках. младшие собственное значение и соответствующую собственную функцию для нек-рых сеточных аналогов эллиптич. задач на собственные значения, при затрате
младшие собственное значение и соответствующую собственную функцию для нек-рых сеточных аналогов эллиптич. задач на собственные значения, при затрате  или даже
или даже  (при
(при 
 ) действий (см. [9]). Пусть задача Рсостоит в решении корректного операторного уравнения
) действий (см. [9]). Пусть задача Рсостоит в решении корректного операторного уравнения
 состоит из таких задач с различными f, при к-рых решения уравнения (2) принадлежат нек-рому компакту U. Обычно Uзадается условием:
состоит из таких задач с различными f, при к-рых решения уравнения (2) принадлежат нек-рому компакту U. Обычно Uзадается условием:
 - нек-рое банахово пространство, вложенное в Н. Если
- нек-рое банахово пространство, вложенное в Н. Если  ищется с точностью
ищется с точностью  в норме Н, то часто известны информационные оценки, равномерные относительно всех
в норме Н, то часто известны информационные оценки, равномерные относительно всех  наименьшей размерности
наименьшей размерности  вектора
вектора  задание к-рого позволяет получить элемент
задание к-рого позволяет получить элемент

 вектора
вектора  (см. [4]) являются
(см. [4]) являются  -аппроксимациями в Нрешения уравнения (2), причем
-аппроксимациями в Нрешения уравнения (2), причем  , где k- константа, не зависящая от
, где k- константа, не зависящая от  (см. [6] - [8], [10], [17]). Если не учитывать работу на формирование (5), то такие методы приводят к оценкам затраты вычислительной работы, минимальным по порядку. Напр., для случая эллиптич. уравнения 2-го порядка
(см. [6] - [8], [10], [17]). Если не учитывать работу на формирование (5), то такие методы приводят к оценкам затраты вычислительной работы, минимальным по порядку. Напр., для случая эллиптич. уравнения 2-го порядка  - пространство С. Л. Соболева [20]), если
- пространство С. Л. Соболева [20]), если  - область на плоскости, достижимы оценки затрат числа арифметич. действий
- область на плоскости, достижимы оценки затрат числа арифметич. действий  Вычислительную работу на формирование (5) тоже часто можно оценить как
Вычислительную работу на формирование (5) тоже часто можно оценить как  , если брать информацию о заданных функциях в соответствующих пространствах. В частности, в упомянутом примере f должна рассматриваться как элемент
, если брать информацию о заданных функциях в соответствующих пространствах. В частности, в упомянутом примере f должна рассматриваться как элемент  , но не
, но не  (см. [8], [17]). Подобного рода оценки получены и для нек-рых дифференциальных задач на собственные значения (см. [9]).
(см. [8], [17]). Подобного рода оценки получены и для нек-рых дифференциальных задач на собственные значения (см. [9]).