|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МИНИМАЛЬНЫХ НЕВЯЗОК МЕТОДЗначение МИНИМАЛЬНЫХ НЕВЯЗОК МЕТОД в математической энциклопедии: - итерационный метод решения линейного операторного уравнения
с самосопряженным положительно определенным ограниченным оператором А, действующим в гильбертовом пространстве Н, и заданным элементом
где параметр
выбирается на каждом шаге
Если спектр оператора Апринадлежит отрезку [ т, М]действительной оси, где Различные способы определения в H скалярного произведения приводят к различным итерационным методам. В частности, при специальных скалярных произведениях формулы М. н. м. совпадают с формулами наискорейшего спуска метода и метода минимальных ошибок (см. [2]). Условия сходимости М. н. м. могут быть ослаблены по сравнению с перечисленными выше: если рассматривать на нек-рых подмножествах из H. Напр., если рассматривать М. н. м. только в действительных пространствах, то можно отказаться от требования самосопряженности оператора А(см. [3], [4]). Лит.:[1] Красносельский М. А., Крейн С. Г., "Матем. сб.", .1952, № 31, с. 315-34; [2] Приближенное решение операторных уравнений, М., 1969; [3] Самарский А. А., Введение в теорию разностных схем, М., 1971; [4] Марчук Г. И., Кузнецов Ю. А., Итерационные методы и квадратичные функционалы, Новосиб., 1972. Ю. А. Кузнецов. |
|
|
|


 . Формулы М. н. м. имеют вид
. Формулы М. н. м. имеют вид

 из условия максимальной минимизации нормы невязки
из условия максимальной минимизации нормы невязки  т. е. требуется выполнение соотношения
т. е. требуется выполнение соотношения
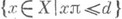 - положительные числа, то последовательные приближения
- положительные числа, то последовательные приближения  метода (2) -(3) сходятся к решению
метода (2) -(3) сходятся к решению  уравнения (1) со скоростью геометрич. прогрессии со знаменателем
уравнения (1) со скоростью геометрич. прогрессии со знаменателем 