|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МИНИМАЛЬНЫХ ИТЕРАЦИЙ МЕТОДЗначение МИНИМАЛЬНЫХ ИТЕРАЦИЙ МЕТОД в математической энциклопедии: - метод решения системы линейных алгебраич. уравнений Ах=b, в к-ром решение xпредставляется в виде линейной комбинации базисных векторов, ортогональных в нек-рон метрике, связанной с матрицей системы. В случае симметричной матрицы Аортогональная система векторов p0, р 1 ..., pn-1 строится по трехчленным рекуррентным формулам pn+1=Apk -akpk -bkpk-1 , k=1, 2, ..., n- 2, (1) p1=Ap0-aop, p0- произвольный вектор, где ak=(Apk , pk)/(pk ,pk ),k=1, 2, ..., n- 2, bk=(pk ,pk )/(pk -1 , pk-1 ),k=1, 2, ..., n- 2. Решение системы
В случае вырождения в алгоритме ортогонализации, т. е. когда р 2=0 при Для случая несимметричной матрицы разработан биортогональный алгоритм. Если матрица Асимметрична и положительно определена, то построение А-ортогональной системы векторов
позволяет избежать решения вспомогательной системы (2) и получить явное выражение для коэффициентов
причем х=х п_1. Такая модификация метода не требует повторного использования всех векторов р 0 , р1, . . ., pk-1.M. и. м. используется также для решения полной проблемы собственных значении и для нахождения обратной матрицы. Лит.:[1] Lanсzоs С, "J. Res. Nat. Bur. Stand.", 1950, v. 45, №4, p. 255-88; [2] Фаддеев Д. К., Фаддеева В. Н., Вычислительные методы линейной алгебры, М., 1960. Е. С. Николаев. |
|
|
|

 находится по формулам
находится по формулам 
 а коэффициенты с k дают решение системы
а коэффициенты с k дают решение системы
 , выбирают новый начальный вектор
, выбирают новый начальный вектор  ортогональный
ортогональный  и достраивают систему базисных векторов до полной системы.
и достраивают систему базисных векторов до полной системы. по формулам (1) с
по формулам (1) с
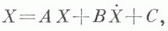 При этом методу A-минимальных, итераций можно придать итерационную форму
При этом методу A-минимальных, итераций можно придать итерационную форму