|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МИНИМАКСНОСТЬ СТАТИСТИЧЕСКОЙ ПРОЦЕДУРЫЗначение МИНИМАКСНОСТЬ СТАТИСТИЧЕСКОЙ ПРОЦЕДУРЫ в математической энциклопедии: - один из вариантов оптимальности в математич. статистике, согласно к-рому статистич. процедура объявляется оптимальной в минимаксном смысле, если она минимизирует максимальный риск. В терминах решающих функций понятие М. с. п. определяется следующим образом. Пусть случайная величина Xпринимает значения в выборочном пространстве (
где
- функция риска, отвечающая статистич. процедуре (решающему правилу)
показывает ожидаемые потери, к-рые можно понести при использовании процедуры
Понятие М. с. п. является полезным в задачах принятия статистич. решении в условиях отсутствия априорной информации относительно параметра Лит.:[1] Леман Э., Проверка статистических гипотез, пер. с англ., 2 изд., М., 1979; [2] 3акс Ш., Теория статистических выводов, пер. с англ., М., 1975. М. С. Никулин |
|
|
|

 ,
,  ),
), , и пусть
, и пусть  - класс решающих функций, с помощью к-рых по реализации случайной величины Xнадлежит выбрать решение d из пространства решений D, т. е.
- класс решающих функций, с помощью к-рых по реализации случайной величины Xнадлежит выбрать решение d из пространства решений D, т. е. при этом задана некрая функция потерь L(a, d), определенная на
при этом задана некрая функция потерь L(a, d), определенная на  В таком случае статистич. процедура
В таком случае статистич. процедура  наз. минимаксной в задаче принятия статистич. решения относительно функции потерь
наз. минимаксной в задаче принятия статистич. решения относительно функции потерь  , если при всех
, если при всех  выполняется соотношение
выполняется соотношение

 , при этом решение
, при этом решение  , отвечающее наблюденной реализации
, отвечающее наблюденной реализации  и минимаксной процедуре
и минимаксной процедуре  , наз. минимаксным. Так как величина
, наз. минимаксным. Так как величина 
 , то М. с. п.
, то М. с. п. означает, что если руководствоваться процедурой
означает, что если руководствоваться процедурой  в задаче выбора решения dиз пространства решений D, то наибольший ожидаемый риск
в задаче выбора решения dиз пространства решений D, то наибольший ожидаемый риск  будет настолько малым, насколько это возможно. Принцип М. с. п. не всегда приводит к разумным выводам (см. рис.); в данном случае следует ориентироваться на процедуру
будет настолько малым, насколько это возможно. Принцип М. с. п. не всегда приводит к разумным выводам (см. рис.); в данном случае следует ориентироваться на процедуру  , а не на
, а не на  , хотя
, хотя 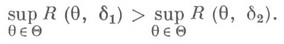

 .
.