"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МИЛНОРА СФЕРА
Значение МИЛНОРА СФЕРА в математической энциклопедии:
- гладкое многообразие, гомео-морфное (кусочно линейно изоморфное) сфере S", но не диффеоморфное ей. Впервые пример такого многообразия был построен Дж. Милнором в 1956 (см. [1]); этот же пример - первый пример гомеоморфных, но не диффеоморфных многообразий.
Построение М. с. Любое гладкое замкнутое многообразие, гомотопически эквивалентное сфере S", при  гомеоморфно (и даже кусочно линейно изоморфно) сфере
гомеоморфно (и даже кусочно линейно изоморфно) сфере  (см. Пуанкаре гипотеза обобщенная, h-кобпрдизм). Сигнатура замкнутого гладкого почти параллелизуемого многообразия размерности
(см. Пуанкаре гипотеза обобщенная, h-кобпрдизм). Сигнатура замкнутого гладкого почти параллелизуемого многообразия размерности  делится на число sk , экспоненциально растущее с ростом k. Для любого кимеется параллелизуемое многообразие
делится на число sk , экспоненциально растущее с ростом k. Для любого кимеется параллелизуемое многообразие  сигнатуры 8 (именно, древовидное многообразие Милнора), край к-рого
сигнатуры 8 (именно, древовидное многообразие Милнора), край к-рого  есть при
есть при  гомотопическая сфера (см. [2]). Если бы Мбыло диффеоморфно сфере
гомотопическая сфера (см. [2]). Если бы Мбыло диффеоморфно сфере  , то многообразие
, то многообразие  , полученное из
, полученное из  добавлением конуса над краем, было бы гладким почти параллелизуемым замкнутым многообразием сигнатуры 8. Таким образом, Месть М. с.
добавлением конуса над краем, было бы гладким почти параллелизуемым замкнутым многообразием сигнатуры 8. Таким образом, Месть М. с.
Имеется и др. пример М. с. (см. [5]).
Классификация М. с. Имеется 28 различных (не диффеоморфных) 7-мерных М. с. (в эти 28 многообразий включена стандартная сфера S 7, и в дальнейшем термин "М. с." используется и для обозлачения стандартной сферы S n).
Множество всех гладкостей на кусочно линейной сфере (точнее, сглаживаний, но для сфер это одно и то же) эквивалентно множеству элементов группы  Последняя группа при i<7 тривиальна, так что любая М. с. размерности, меньшей 7, диффеоморфна стандартной.
Последняя группа при i<7 тривиальна, так что любая М. с. размерности, меньшей 7, диффеоморфна стандартной.
Пусть  - множество классов h-кобордантности n-мерных гладких многообразии, гомотопически эквивалентных сфере S n. Операция связной суммы превращает это множество в группу, где нуль - класс h- кобордантности сферы Sn. При n>5 элементы группы qn находятся во взаимно однозначном соответствии с классами диффеоморфности n-мерных М. с. Для вычисления групп qn n>5, задается (см. [3]) тривиализация стабильного нормального расслоения (оснащение) М. с. М п. Это возможно, так как М п стабильно параллелизуемо. Полученное оснащенное многообразие определяет элемент стабильной гомотопич. группы
- множество классов h-кобордантности n-мерных гладких многообразии, гомотопически эквивалентных сфере S n. Операция связной суммы превращает это множество в группу, где нуль - класс h- кобордантности сферы Sn. При n>5 элементы группы qn находятся во взаимно однозначном соответствии с классами диффеоморфности n-мерных М. с. Для вычисления групп qn n>5, задается (см. [3]) тривиализация стабильного нормального расслоения (оснащение) М. с. М п. Это возможно, так как М п стабильно параллелизуемо. Полученное оснащенное многообразие определяет элемент стабильной гомотопич. группы 

Этот элемент зависит, вообще говоря, от выбора оснащения ( - "многозначное отображение"). Пусть
- "многозначное отображение"). Пусть  - подгруппа в
- подгруппа в  , состоящая из М. с, ограничивающих параллелизуемые многообразия. Построенное многозначное отображение индуцирует гомоморфизм
, состоящая из М. с, ограничивающих параллелизуемые многообразия. Построенное многозначное отображение индуцирует гомоморфизм  где
где  - стационарный Уайтхеда гомоморфизм и
- стационарный Уайтхеда гомоморфизм и  -изоморфизм. Вычисление группы
-изоморфизм. Вычисление группы 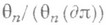 сводится к задаче (нерешенной, 1982) вычисления группы
сводится к задаче (нерешенной, 1982) вычисления группы  и вычисления группы
и вычисления группы  что делается посредством Морса перестроек пленки (при сохранении края). Пусть
что делается посредством Морса перестроек пленки (при сохранении края). Пусть  , то есть
, то есть  и
и  параллелизуемо. Если W- стягиваемое многообразие, то после вырезания в Wмаленького диска многообразие М h -кобордантно
параллелизуемо. Если W- стягиваемое многообразие, то после вырезания в Wмаленького диска многообразие М h -кобордантно  , то есть
, то есть  . Если пчетно, то можно так изменить Wпосредством перестроек Морса, что новое многообразие
. Если пчетно, то можно так изменить Wпосредством перестроек Морса, что новое многообразие  будет стягиваемым (здесь требуется параллелизуемость многообразия Wи условие n>5). Итак,
будет стягиваемым (здесь требуется параллелизуемость многообразия Wи условие n>5). Итак,
Случай n+1 = 4k. Если сигнатура s(W). многообразия Wесть 0, то Wможно перестройками Морса превратить в стягиваемое многообразие, так что в этом случае Месть стандартная сфера. Если M=дW и M' = дW, то 
 (здесь
(здесь  - связная сумма многообразий А и В). Если
- связная сумма многообразий А и В). Если  , то
, то  , так что инвариант
, так что инвариант  однозначно определяет элемент
однозначно определяет элемент  Если
Если  и
и  то
то  делится на
делится на  . Обратно, для любого
. Обратно, для любого  существует гладкое замкнутое многообразие
существует гладкое замкнутое многообразие  с
с  поэтому если
поэтому если  и
и  то
то  гле
гле 
 параллелизуемо и
параллелизуемо и 
Элемент  полностью определяется вычетом
полностью определяется вычетом 
 , и разные вычеты определяют разные многообразия. Так как
, и разные вычеты определяют разные многообразия. Так как  принимает любое значение, кратное 8, то
принимает любое значение, кратное 8, то 
Случай n=4k+1. Пусть  . Если Кервера инвариант многообразия Wесть нуль, то есть
. Если Кервера инвариант многообразия Wесть нуль, то есть  , то Wперестраивается до стягиваемого многообразия, то есть [M] = 0. Пусть теперь
, то Wперестраивается до стягиваемого многообразия, то есть [M] = 0. Пусть теперь  Так как при
Так как при  не существует гладкого замкнутого почти параллелизуемого (что в размерности
не существует гладкого замкнутого почти параллелизуемого (что в размерности  равносильно параллелизуемости) многообразия с инвариантом Кервера, не равным нулю, то Мне диффеоморфно
равносильно параллелизуемости) многообразия с инвариантом Кервера, не равным нулю, то Мне диффеоморфно  В этом случае
В этом случае  то есть
то есть 
При  и тех значениях i, где существует многообразие с ненулевым инвариантом Кервера,
и тех значениях i, где существует многообразие с ненулевым инвариантом Кервера,  , то есть
, то есть  но вопрос об описании всех таких не решен (1982), хотя при
но вопрос об описании всех таких не решен (1982), хотя при  ответ положителен. Итак,
ответ положителен. Итак,  есть
есть  или 0.
или 0.
Имеется другое представление М. с. Пусть в пространстве  W- алгебраическое многообразие с уравнением
W- алгебраическое многообразие с уравнением

и  есть (2п+1)-мерная сфера радиуса e(малого) с центром в начале координат. При подходящих значениях
есть (2п+1)-мерная сфера радиуса e(малого) с центром в начале координат. При подходящих значениях  есть М. с. (см. [4]). Напр., при n=4 и a1=6k-1, а 2=3, a3=a4=a5=2 и k=1, 2, . . ., 28 получаются все 28 7-мерных М. с.
есть М. с. (см. [4]). Напр., при n=4 и a1=6k-1, а 2=3, a3=a4=a5=2 и k=1, 2, . . ., 28 получаются все 28 7-мерных М. с.
Лит.:[1] Милнор Дж .,"Математика", 1957, т. 1, № 3, с. 35-42; [2] Мilnоr j., Kervaire М., в кн.: Proceedings of the International Congress of Mathematicians, 1958, Camb., 1960, p. 454 - 58; [3] их же, "Ann. Math.", 1963, v. 77, № 3, p. 504-37: [4] Mилнор Дж., Особые точки комплексных гиперповерхностей, пер. с англ., М., 1971; [5] Милнор Д ж., Сташеф Дж., Характеристические классы, пер. с англ., М., 1979. Ю. Б. Рудяк.

 гомеоморфно (и даже кусочно линейно изоморфно) сфере
гомеоморфно (и даже кусочно линейно изоморфно) сфере  (см. Пуанкаре гипотеза обобщенная, h-кобпрдизм). Сигнатура замкнутого гладкого почти параллелизуемого многообразия размерности
(см. Пуанкаре гипотеза обобщенная, h-кобпрдизм). Сигнатура замкнутого гладкого почти параллелизуемого многообразия размерности  делится на число sk , экспоненциально растущее с ростом k. Для любого кимеется параллелизуемое многообразие
делится на число sk , экспоненциально растущее с ростом k. Для любого кимеется параллелизуемое многообразие  сигнатуры 8 (именно, древовидное многообразие Милнора), край к-рого
сигнатуры 8 (именно, древовидное многообразие Милнора), край к-рого  есть при
есть при  гомотопическая сфера (см. [2]). Если бы Мбыло диффеоморфно сфере
гомотопическая сфера (см. [2]). Если бы Мбыло диффеоморфно сфере  , то многообразие
, то многообразие  , полученное из
, полученное из  добавлением конуса над краем, было бы гладким почти параллелизуемым замкнутым многообразием сигнатуры 8. Таким образом, Месть М. с.
добавлением конуса над краем, было бы гладким почти параллелизуемым замкнутым многообразием сигнатуры 8. Таким образом, Месть М. с. Последняя группа при i<7 тривиальна, так что любая М. с. размерности, меньшей 7, диффеоморфна стандартной.
Последняя группа при i<7 тривиальна, так что любая М. с. размерности, меньшей 7, диффеоморфна стандартной. - множество классов h-кобордантности n-мерных гладких многообразии, гомотопически эквивалентных сфере S n. Операция связной суммы превращает это множество в группу, где нуль - класс h- кобордантности сферы Sn. При n>5 элементы группы qn находятся во взаимно однозначном соответствии с классами диффеоморфности n-мерных М. с. Для вычисления групп qn n>5, задается (см. [3]) тривиализация стабильного нормального расслоения (оснащение) М. с. М п. Это возможно, так как М п стабильно параллелизуемо. Полученное оснащенное многообразие определяет элемент стабильной гомотопич. группы
- множество классов h-кобордантности n-мерных гладких многообразии, гомотопически эквивалентных сфере S n. Операция связной суммы превращает это множество в группу, где нуль - класс h- кобордантности сферы Sn. При n>5 элементы группы qn находятся во взаимно однозначном соответствии с классами диффеоморфности n-мерных М. с. Для вычисления групп qn n>5, задается (см. [3]) тривиализация стабильного нормального расслоения (оснащение) М. с. М п. Это возможно, так как М п стабильно параллелизуемо. Полученное оснащенное многообразие определяет элемент стабильной гомотопич. группы 

 - "многозначное отображение"). Пусть
- "многозначное отображение"). Пусть  - подгруппа в
- подгруппа в  , состоящая из М. с, ограничивающих параллелизуемые многообразия. Построенное многозначное отображение индуцирует гомоморфизм
, состоящая из М. с, ограничивающих параллелизуемые многообразия. Построенное многозначное отображение индуцирует гомоморфизм  где
где  - стационарный Уайтхеда гомоморфизм и
- стационарный Уайтхеда гомоморфизм и  -изоморфизм. Вычисление группы
-изоморфизм. Вычисление группы 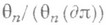 сводится к задаче (нерешенной, 1982) вычисления группы
сводится к задаче (нерешенной, 1982) вычисления группы  и вычисления группы
и вычисления группы  что делается посредством Морса перестроек пленки (при сохранении края). Пусть
что делается посредством Морса перестроек пленки (при сохранении края). Пусть  , то есть
, то есть  и
и  параллелизуемо. Если W- стягиваемое многообразие, то после вырезания в Wмаленького диска многообразие М h -кобордантно
параллелизуемо. Если W- стягиваемое многообразие, то после вырезания в Wмаленького диска многообразие М h -кобордантно  , то есть
, то есть  . Если пчетно, то можно так изменить Wпосредством перестроек Морса, что новое многообразие
. Если пчетно, то можно так изменить Wпосредством перестроек Морса, что новое многообразие  будет стягиваемым (здесь требуется параллелизуемость многообразия Wи условие n>5). Итак,
будет стягиваемым (здесь требуется параллелизуемость многообразия Wи условие n>5). Итак,

 (здесь
(здесь  - связная сумма многообразий А и В). Если
- связная сумма многообразий А и В). Если  , то
, то  , так что инвариант
, так что инвариант  однозначно определяет элемент
однозначно определяет элемент  Если
Если  и
и  то
то  делится на
делится на  . Обратно, для любого
. Обратно, для любого  существует гладкое замкнутое многообразие
существует гладкое замкнутое многообразие  с
с  поэтому если
поэтому если  и
и  то
то  гле
гле 
 параллелизуемо и
параллелизуемо и 
 полностью определяется вычетом
полностью определяется вычетом 
 , и разные вычеты определяют разные многообразия. Так как
, и разные вычеты определяют разные многообразия. Так как  принимает любое значение, кратное 8, то
принимает любое значение, кратное 8, то 
 . Если Кервера инвариант многообразия Wесть нуль, то есть
. Если Кервера инвариант многообразия Wесть нуль, то есть  , то Wперестраивается до стягиваемого многообразия, то есть [M] = 0. Пусть теперь
, то Wперестраивается до стягиваемого многообразия, то есть [M] = 0. Пусть теперь  Так как при
Так как при  не существует гладкого замкнутого почти параллелизуемого (что в размерности
не существует гладкого замкнутого почти параллелизуемого (что в размерности  равносильно параллелизуемости) многообразия с инвариантом Кервера, не равным нулю, то Мне диффеоморфно
равносильно параллелизуемости) многообразия с инвариантом Кервера, не равным нулю, то Мне диффеоморфно  В этом случае
В этом случае  то есть
то есть 
 и тех значениях i, где существует многообразие с ненулевым инвариантом Кервера,
и тех значениях i, где существует многообразие с ненулевым инвариантом Кервера,  , то есть
, то есть  но вопрос об описании всех таких не решен (1982), хотя при
но вопрос об описании всех таких не решен (1982), хотя при  ответ положителен. Итак,
ответ положителен. Итак,  есть
есть  или 0.
или 0. W- алгебраическое многообразие с уравнением
W- алгебраическое многообразие с уравнением
 есть (2п+1)-мерная сфера радиуса e(малого) с центром в начале координат. При подходящих значениях
есть (2п+1)-мерная сфера радиуса e(малого) с центром в начале координат. При подходящих значениях  есть М. с. (см. [4]). Напр., при n=4 и a1=6k-1, а 2=3, a3=a4=a5=2 и k=1, 2, . . ., 28 получаются все 28 7-мерных М. с.
есть М. с. (см. [4]). Напр., при n=4 и a1=6k-1, а 2=3, a3=a4=a5=2 и k=1, 2, . . ., 28 получаются все 28 7-мерных М. с.