|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МЕТРИЧЕСКОЕ ПРОСТРАНСТВОЗначение МЕТРИЧЕСКОЕ ПРОСТРАНСТВО в математической энциклопедии: - множество Xвместе с нек-рой метрикойr на ном. Теоретико-множественный подход к изучению фигур (пространств) основан на исследовании взаимного расположения составляющих их элементарных частей. Одной из фундаментальных характеристик взаимного расположения точек пространства является расстояние между ними. Этот подход к пространственным отношениям и приводит к понятию М. п., впервые выделенному М. Фрепте [2] в связи с рассмотрением функциональных пространств. Оказалось, что естественную метрику несут на себе множества объектов самой разной природы. Как М. <п. могут рассматриваться множества состояний, функций и отображений, любые подмножества евклидовых пространств и гильбертова пространства. Рассмотрение метрик важно при исследовании сходимости (рядов, функций), при решении вопросов аппроксимации. Развитие теории М. п. шло по следующим важнейшим направлениям. Общая теория М. п. В ней исследуются свойства М. п., инвариантные относительно изометрий - взаимно однозначных отображений на, сохраняющих расстояние. К числу таких свойств относятся полнота, ограниченность, вполне ограниченность, диаметр. Свойства этого типа наз. метрическими. Топологическая теория М. <п. Предметом ее являются свойства М. п., сохраняющиеся при гомеоморфизмах. Среди них - компактность, сепарабельность, связность, свойство Бэра, нульмерность. Свойства этого типа наз. топологическими. Теория пространств, на к-рых задана метрика, согласованная с какой-либо дополнительной алгебраич. структурой (напр., векторного пространства или группы). Сюда относятся евклидовы пространства, предгильбертовы и гильбертовы пространства (любого веса), банаховы пространства, банаховы алгебры, банаховы решетки, счетно нормированные пространства. Имеющиеся здесь факты существенно связаны с рассмотрением важных в идей ном отношении свойств метрик или норм, но по содержанию целиком принадлежат соответствующим областям алгебры и функционального анализа. Рассмотрение специальных метрик играет важную роль при исследовании неевклидовых геометрий, в дифференциальной геометрии, механике и физике. Центральное место здесь занимает понятие римановой метрики риманова пространства (см. Риманова геометрия). Более широкий подход к изучению поверхностей и фигур, возникающих в дифференциальной геометрии, связан с концепцией G-пространства, получающейся добавлением к аксиомам метрики нек-рых условий (см. Геодезических геометрия), создающих основу для рассмотрения геодезических в G-пространстве, обеспечивая их существование и правильные свойства. Характерным здесь является отказ от пользования методами дифференциального исчисления, при этом обнаруживается, что многое в дифференциальной геометрии не связано с условиями дифференцируемости, а определяется только геометрич. аксиомами. Геометрия геодезических представляет интерес не только как обобщение римановой геометрии, но и как попытка заменить вычисления рассуждениями, сделать исследование геометрич. объектов более геометричным. На каждом множестве Xможет быть определена метрика Точка хобъявляется абсолютно близкой ко множеству А, если В исследовании М. п. (особенно их топологич. свойств) важная роль принадлежит понятию сходящейся последовательности. Это объясняется тем, что топология каждого М. п. может быть полностью описана на языке последовательностей. Пусть Важным метрич. свойством является полнота - М. п. Примерами полных М. п. могут служить евклидовы и банаховы пространства. Важным свойством полных М. п., сохраняющимся при гомеоморфизмах, является Бэра свойство, в силу к-рого каждое полное М. п. без изолироваяных точек несчетно. Поэтому обычная топология пространства рациональных чисел не порождается никакой полной метрикой. Однако каждое М. <П. может быть представлено как часть нек-рого полного М. п. посредством стандартной конструкции пополнения. Две фундаментальные последовательности Пусть Метрика
Для С рассмотрением пополнений связана Лаврентьева теорема о продолжении гомеоморфизмов. Из нее следует, что свойство М. п. быть множеством типа Метрики Важен следующий пример полного М. п.: пространство
для всех Подмножество У полного М. п. Существует фундаментальная связь между понятиями полноты и компактности М. п. Компактность М. п. X, р равносильна любому из следующих условий: 1) любая последовательность в 4) каждая убывающая последовательность непустых замкнутых в Простейшие примеры компактных М. п.: конечные дискретные пространства, любой отрезок (с концами), квадрат, окружность, сфера. Вообще, подпространство евклидова пространства Не все из перечисленных условий равносильны за пределами класса М. п. (см. Бикомпактное пространство). А. Лебег (Н. Lebesgue, 1911) установил, что для каждого открытого покрытия Каждое компактное М. п. полно, но обратное неверно; простейшим примером служит бесконечное дискретное пространство, наделенное тривиальной метрикой. Но имеет место следующая характеристика: М. п. компактно в том и только в том случае, если всякое гомеоморфное ему М. п. полно. Интуитивно очевидно, что компактность включает, помимо полноты, условие типа ограниченности, что подтверждается рассмотрением компактных подпространств в Важную роль в функциональном анализе играет критерий компактности произвольного множества Анепрерывных функций, определенных на отрезке Отображение f М. п. Топологич. теория М. п. значительно проще общей теории топологич. пространств. Ниже приводятся наиболее важные топологич. свойства М. п. Исследование топологич. свойств М. п. в большей степени основывается на следующей теореме Стоуна: М. п. паракомпактно, т. о. в любое его открытое покрытие g можно вписать локально конечное открытое покрытие l(локальная конечность означает наличие у каждой точки окрестности, задевающей лишь конечное множество элементов покрытия l). На теореме о паракомпактности М. п. основан метризационный критерий Нагаты - Смирнова (см. Метризуемое пространство). Для М. п. имеют место важные теоремы об эквивалентности топологич. свойств, различаемых в рамках общей топологии. Так, совпадают следующие карди-нальнозначные инварианты: плотность, вес, число Суслина, число Линделёфа. Для М. п. равносильны: счетная компактность, псевдокомпактность и бикомпактность. Для М. п. совпадают размерности dim (в смысле покрытий) и Ind (большая индуктивная), а для сепарабельных М. п. с dim и Ind совпадает и малая индуктивная размерность ind (см. Размерности теория). Каждое М. п. М. п. может не иметь счетной базы, но всегда удовлетворяет первой аксиоме счетности - имеет счетную базу в каждой точке. Более того, каждый компакт в М. п. имеет счетную базу окрестностей. Сверх того, в каждом М. п. существует такая база, что каждая точка пространства принадлежит лишь счетному множеству ее элементов - точечно-счетная база, но это свойство слабее метризуемости даже в присутствии паракомпактности и хаусдорфовости. Не обязано быть метризуемым и регулярное сепарабельное пространство с первой аксиомой счетности. Просто выглядит условие метризуемости отделимой топологич. группы - для этого необходимо и достаточно, чтобы пространство группы удовлетворяло первой аксиоме счетности, причем на группе тогда существуют как левоинвариантная, так и правоинвариантная метрики, порождающие ее топологию. С каждым М. п.
Пространство Непрерывный образ М. п. может быть не гомеоморфен никакому М. п., даже удовлетворяя аксиоме отделимости Хаусдорфа. Это относится и к факторпространствам М. п. Напр., если на плоскости "склеить" в точку фиксированную прямую, взяв в качестве отдельных элементов разбиения все точки плоскости, не попавшие на эту прямую, то получится неметризуемое нормальное сепарабельное пространство - в особой его точке не выполняется первая аксиома счетности. Имеется общий критерий метризуемости факторпространства М. п. (см. 16]). В частности, пространство непрерывного разбиения М. п. на компакты всегда метризуемо. Всякое хаусдорфово пространство, являющееся непрерывным образом компактного М. п., метризуемо и компактно - это частное проявление общего положения о неповышении веса топологич. пространства при непрерывном отображении на бикомпакт. Но и когда образ YМ. п.
если и только если Топологич. пространство, являющееся образом М. п. при непрерывном, открытом и замкнутом отображении, само гомеоморфно нек-рому М. п. Однако при непрерывных открытых отображениях метризуемость сохраняется не всегда - все пространства с первой аксиомой счетности и только они представимы как образы М. п. при непрерывных открытых отображениях. Среди обобщений М. п. наиболее важны псевдометрич. пространства, пространства с симметрикой и пространства с 0-метрикой [7]. Они определяются аксиоматически посредством естественных ослаблений системы аксиом М. п. Но расстояние здесь по-прежнему выражается неотрицательной действительным числом. Можно рассматривать обобщенные метрики со значениями в упорядоченных полугруппах, полуполях и т. д. (см. [8]). На этом пути можно осуществить обобщенную метризацию произвольного вполне регулярного пространства. Фундаментальным обобщением концепции М. п. является понятие равномерного пространства. Далее идут чисто топологич. расширения класса М. п., среди к-рых важны классы пространств с равномерной базой, моровских пространств, перистых и паракомпактных перистых пространств, кружевных пространств. Класс паракомпактов является слишком широким обобщением класса М. п., чтобы считаться таковым: паракомпактность не сохраняется даже при возведении в квадрат. Напротив, класс паракомпактных перистых пространств является удачным одновременным обобщением класса пространств, гомеоморфных М. п., и класса бикомпактов. В ином направлении обобщают понятие метрики х-метрики и б-метрики [4]. Концепция стати-стич. М. п., введенная К. Менгером (К. Menger), в топологич. отношении оказалась равноценной понятию пространства с симметрикой. Лит.:[1] Александров П. С, Введение в теорию множеств и общую топологию, М., 1977; [2] Frechet M., "Rend. Circolo mat. Palermo", 1906, v. 22; [3] Архангельский А. В., Пономарев В. И., Основы общей топологии в задачах и упражнениях, М., 1974; [4] Щепин Е. В., "Успехи матем. наук", 1976, т. 31, в. 5, с. 191-226; [5] Еngelking R., General topology, Warsz., 1977; [6] Apxангельcкий А. В., "Докл. АН СССР", 1964, т.155, №2, с. 247-50; [7] Недев С. Й., "Тр. Моск. матем. об-ва", 1971, т. 24, с. 201--36; [81 Антоновский М. Я., Болтянский В. Г., Сарымсаков Т. А., "Успехи матем. наук", 1966, т. 21, в. 4, с. 185-218; [9] Недев С. Й., Чобан М. М., "Сердика", 1975, т. 1, с. 12-28. А. В. Архангельский. |
|
|
|

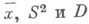 по следующему правилу:
по следующему правилу:  если
если  , и
, и  , если
, если 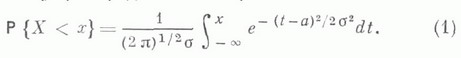 Эта метрика наз. тривиальной. Каждая метрика
Эта метрика наз. тривиальной. Каждая метрика  на множестве Xпозволяет естественным образом ввести на Xтопологию
на множестве Xпозволяет естественным образом ввести на Xтопологию  Концепция топологич. пространства заключает в себе аксиоматизацию отношения абсолютной близости точки к множеству, тогда как концепцией М. п. формализуется отношение сравнительной близости между точками. Расстояние
Концепция топологич. пространства заключает в себе аксиоматизацию отношения абсолютной близости точки к множеству, тогда как концепцией М. п. формализуется отношение сравнительной близости между точками. Расстояние  от точки хдо множества Ав М. п.
от точки хдо множества Ав М. п.  определяется как
определяется как 
 . Замыканием [А]множества Ав
. Замыканием [А]множества Ав  наз. множество всех точек из X, абсолютно близких к А. Однозначно отвечающая этой операции топология на множестве X и наз. топологией, порожденной на X метрикой
наз. множество всех точек из X, абсолютно близких к А. Однозначно отвечающая этой операции топология на множестве X и наз. топологией, порожденной на X метрикой  . Тривиальной метрике на Xотвечает дискретная топология - все множества замкнуты.
. Тривиальной метрике на Xотвечает дискретная топология - все множества замкнуты. - последовательность точек в М. п.
- последовательность точек в М. п.  . Она наз. сходящейся к точке
. Она наз. сходящейся к точке  , если для каждого
, если для каждого  найдется целое число Nтакое, что
найдется целое число Nтакое, что  при всех
при всех 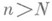 . Последовательность
. Последовательность  наз. фундаментальной, если для каждого
наз. фундаментальной, если для каждого  найдется целое число Nтакое, что
найдется целое число Nтакое, что  при всех т, n>N.
при всех т, n>N. наз. полным, если каждая фундаментальная последовательность в нем сходится к нек-рой его точке. Пространство
наз. полным, если каждая фундаментальная последовательность в нем сходится к нек-рой его точке. Пространство  полно. Полнота М. п. не является топологич. свойством: М. п., гомеоморфное полному М. п., может не быть полным, напр, действительная прямая
полно. Полнота М. п. не является топологич. свойством: М. п., гомеоморфное полному М. п., может не быть полным, напр, действительная прямая  с обычной метрикой
с обычной метрикой  гомеоморфна интервалу
гомеоморфна интервалу  , наделенному той же метрикой, однако первое М. п. полно, а второе - нет.
, наделенному той же метрикой, однако первое М. п. полно, а второе - нет.
 в М. п.
в М. п.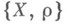 наз. эквивалентными, если
наз. эквивалентными, если 
 - множество всех возникающих классов эквивалентности.
- множество всех возникающих классов эквивалентности. на
на  вводится правилом:
вводится правилом: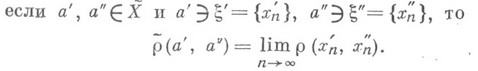
 пусть
пусть  , где
, где  при всех
при всех  . Тогда
. Тогда  - полное М. п. и
- полное М. п. и  - изометрич. отображение пространства
- изометрич. отображение пространства  на всюду плотное подпространство в
на всюду плотное подпространство в  (в связи с чем
(в связи с чем  и наз. пополнением пространства
и наз. пополнением пространства  ).
). в своем пополнении топологически инвариантно (в отличие от неинвариантности самой метрич. полноты относительно гомеоморфизмов).
в своем пополнении топологически инвариантно (в отличие от неинвариантности самой метрич. полноты относительно гомеоморфизмов). и
и  на множестве Xназ. топологически эквивалентными, если совпадают порожденные ими топологии
на множестве Xназ. топологически эквивалентными, если совпадают порожденные ими топологии  и
и  . На конечном множестве все метрики эквивалентны - он порождают дискретную топологию. Теорема Александрова - Хаусдорфа: метрика
. На конечном множестве все метрики эквивалентны - он порождают дискретную топологию. Теорема Александрова - Хаусдорфа: метрика  на множестве Xтопологически эквивалентна нек-рой полной метрике в том и только в том случае, если Xявляется множеством типа Gd в пополнении М. п.
на множестве Xтопологически эквивалентна нек-рой полной метрике в том и только в том случае, если Xявляется множеством типа Gd в пополнении М. п. В частности, пространство иррациональных чисел с обычной метрикой (не полное относительно ее) гомео-морфно полному метрич. пространству Бэра, точками к-рого являются всевозможные бесконечные последовательности
В частности, пространство иррациональных чисел с обычной метрикой (не полное относительно ее) гомео-морфно полному метрич. пространству Бэра, точками к-рого являются всевозможные бесконечные последовательности  натуральных чисел, а расстояние задается правилом:
натуральных чисел, а расстояние задается правилом:  где
где  таково, что
таково, что  и
и 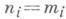 при всех
при всех 
 , составленное из всех непрерывных функций, определенных на отрезке
, составленное из всех непрерывных функций, определенных на отрезке  , и несущее на себе метрику, определенную правилом
, и несущее на себе метрику, определенную правилом
 . Пространство
. Пространство  сепарабельно - в нем есть счетное всюду плотное множество. Оказывается, каждое сепарабельное М. п. изометрично нек-рому подпространству
сепарабельно - в нем есть счетное всюду плотное множество. Оказывается, каждое сепарабельное М. п. изометрично нек-рому подпространству 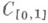 (теорема Банаха - Мазура). Этот результат означает, в частности, что все метрики, порождающие сепарабельные топологии, оправданы (ибо изометричное пространство может быть получено сужением естественной метрики множества непрерывных функций).
(теорема Банаха - Мазура). Этот результат означает, в частности, что все метрики, порождающие сепарабельные топологии, оправданы (ибо изометричное пространство может быть получено сужением естественной метрики множества непрерывных функций). , наделенное той же метрикой
, наделенное той же метрикой  (точнее, ее сужением на
(точнее, ее сужением на  ), является полным М. п., если и только если Y замкнуто в
), является полным М. п., если и только если Y замкнуто в 
 содержит сходящуюся предпоследовательность; 2) каждое счетное открытое покрытие пространства
содержит сходящуюся предпоследовательность; 2) каждое счетное открытое покрытие пространства  содержит конечное подпокрытие; 3) в любом открытом покрытии пространства
содержит конечное подпокрытие; 3) в любом открытом покрытии пространства  найдется конечное подпокрытие;
найдется конечное подпокрытие; множеств имеет непустое пересечение; 5) каждое замкнутое дискретное подпространство пространства
множеств имеет непустое пересечение; 5) каждое замкнутое дискретное подпространство пространства  конечно.
конечно. , взятое в обычной метрике, компактно в том и только в том случае, если оно замкнуто в
, взятое в обычной метрике, компактно в том и только в том случае, если оно замкнуто в  и ограничено.
и ограничено. компактного М. п.
компактного М. п.  существует числотакое,
существует числотакое,  что всякое множество
что всякое множество  диаметра
диаметра  содержится в некотором элементе покрытия
содержится в некотором элементе покрытия  . Отсюда следует фундаментальное свойство компактных М. п., характеризующее их в классе всех М. п.: всякое непрерывное отображение такого пространства в произвольное М. п. равномерно непрерывно. Далее, М. п. компактно в том и только в том случае, если каждая непрерывная действительная функция на нем ограничена (и достигает наименьшего и наибольшего значений).
. Отсюда следует фундаментальное свойство компактных М. п., характеризующее их в классе всех М. п.: всякое непрерывное отображение такого пространства в произвольное М. п. равномерно непрерывно. Далее, М. п. компактно в том и только в том случае, если каждая непрерывная действительная функция на нем ограничена (и достигает наименьшего и наибольшего значений). . В общем случае М. п.
. В общем случае М. п.  наз. ограниченным, если существует действительное число атакое, что
наз. ограниченным, если существует действительное число атакое, что  для всех
для всех  . Каждое компактное М. п. ограничено. Пространство
. Каждое компактное М. п. ограничено. Пространство  полно и ограничено, но не компактно, если Xбесконечно, так что полнота и ограниченность в совокупности недостаточны для компактности М. п. Вообще, всякая метрика на любом множестве топологически эквивалентна нек-рой ограниченной метрике - полной, если заданная метрика полна. В связи с этим получает важное значение понятие вполне ограниченности. М. п.
полно и ограничено, но не компактно, если Xбесконечно, так что полнота и ограниченность в совокупности недостаточны для компактности М. п. Вообще, всякая метрика на любом множестве топологически эквивалентна нек-рой ограниченной метрике - полной, если заданная метрика полна. В связи с этим получает важное значение понятие вполне ограниченности. М. п.  наз. вполне ограниченным, если для каждого
наз. вполне ограниченным, если для каждого  существует конечное множество
существует конечное множество  такое, что
такое, что  при всех
при всех  . Множество
. Множество  наз. при этом
наз. при этом  -сетью в
-сетью в  . М. п.
. М. п. компактно, если и только если оно полно и вполне ограничено, и
компактно, если и только если оно полно и вполне ограничено, и  вполне ограничено в том и только в том случае, если оно изометрично подпространству нек-рого компактного М. п. Точнее, вполне ограниченность М. п.
вполне ограничено в том и только в том случае, если оно изометрично подпространству нек-рого компактного М. п. Точнее, вполне ограниченность М. п.  равносильна компактности его пополнения
равносильна компактности его пополнения  . Каждое подпространство вполне ограниченного М. п. вполне ограничено. Все вполне ограниченные М. п. (в частности, все компактные М. п.) сепарабельны и обладают счетной базой. Компактность, вообще говоря, не наследуется подпространствами; множество
. Каждое подпространство вполне ограниченного М. п. вполне ограничено. Все вполне ограниченные М. п. (в частности, все компактные М. п.) сепарабельны и обладают счетной базой. Компактность, вообще говоря, не наследуется подпространствами; множество  компактно в М. п.
компактно в М. п.  , если замыкание Ав
, если замыкание Ав  является компактным М. п. Если
является компактным М. п. Если  полно, то компактность множества
полно, то компактность множества  в
в  равносильна вполне ограниченности А, наделенного метрикой
равносильна вполне ограниченности А, наделенного метрикой  .
. , в М. п.
, в М. п. , заключенный в следующей теореме Арцела - Асколи: множество Акомпактно в
, заключенный в следующей теореме Арцела - Асколи: множество Акомпактно в  если и только если выполняются условия: 1) существует число Мтакое, что
если и только если выполняются условия: 1) существует число Мтакое, что  при всех
при всех  и всех
и всех  ;.2) для каждого
;.2) для каждого  найдется
найдется  такое, что
такое, что  для всех
для всех  и всех
и всех  для к-рых
для к-рых 
 в себя наз. сжимающим, если существует действительное число
в себя наз. сжимающим, если существует действительное число  такое, что
такое, что  при всех
при всех 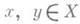 . Важной теоремой о полных М. п. является принцип сжимающих (сжатых) отображений: для каждого такого отображения (непустого) полного М. п.
. Важной теоремой о полных М. п. является принцип сжимающих (сжатых) отображений: для каждого такого отображения (непустого) полного М. п.  в себя существует ровно одна неподвижная точка.
в себя существует ровно одна неподвижная точка. - имеются ввиду свойства топологии
- имеются ввиду свойства топологии  , порожденной метрикой. Каждое М. п. нормально и даже коллективно нормально. Это позволяет продолжать непрерывные действительные функции с замкнутых подмножеств М. п. на все пространство. Более сильное утверждение: для каждого замкнутого подмножества YМ. п.
, порожденной метрикой. Каждое М. п. нормально и даже коллективно нормально. Это позволяет продолжать непрерывные действительные функции с замкнутых подмножеств М. п. на все пространство. Более сильное утверждение: для каждого замкнутого подмножества YМ. п. существует линейное отображение
существует линейное отображение  пространства всех непрерывных действительных функций на
пространства всех непрерывных действительных функций на  в пространство всех непрерывных действительных функций на
в пространство всех непрерывных действительных функций на  такое, что (каково бы ни было f)
такое, что (каково бы ни было f)  является продолжением функции
является продолжением функции  и
и 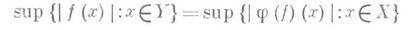 (теорема Дугунджи). Эта теорема связана с теоремой Хаусдорфа о продолжении метрики: если замкнутое подпространство Yметризуемого пространства Xуже метризовано метрикой r1 (порождающей на Y топологию подпространства X), то можно продолжить r1. до метрики р на всем X, порождающей исходную топологию на X. Аналогичные утверждения справедливы для вполне ограниченных метрик и полных метрик.
(теорема Дугунджи). Эта теорема связана с теоремой Хаусдорфа о продолжении метрики: если замкнутое подпространство Yметризуемого пространства Xуже метризовано метрикой r1 (порождающей на Y топологию подпространства X), то можно продолжить r1. до метрики р на всем X, порождающей исходную топологию на X. Аналогичные утверждения справедливы для вполне ограниченных метрик и полных метрик. звездно нормально: в любое открытое покрытие упространства
звездно нормально: в любое открытое покрытие упространства  можно вписать открытое покрытие l. звездно, т. е. так, что для каждой точки
можно вписать открытое покрытие l. звездно, т. е. так, что для каждой точки  найдется
найдется  , содержащее всякое
, содержащее всякое  , для к-рого.
, для к-рого. С этой теоремой связан критерий метризуемости (Стоуна-Архангельского). Критерием метризуемости регулярного пространства вполне ограниченной метрикой является наличие в этом пространстве счетной базы - но даже счетное регулярное пространство может быть не метризуемо. Простейший пример получается присоединением к дискретному натуральному ряду какой-нибудь одной точки из нароста Стоуна- Чеха бикомпактного расширения натурального ряда. Неожиданный характер носит критерий метризуемости метризуемого пространства Xполной метрикой - для этого необходимо и достаточно, чтобы Xбыло множеством типа Gd. в каком-нибудь (а тогда и в любом) бикомпактном хаусдорфовом расширении пространства X. Впрочем, бикомпактные хаусдорфовы расширения М. п. несут полную информацию о топологии последних, как это видно из теоремы Чеха: М. п. гомеоморфны в том и только в том случае, если гомеоморфны их расширения Стоуна - Чеха.
С этой теоремой связан критерий метризуемости (Стоуна-Архангельского). Критерием метризуемости регулярного пространства вполне ограниченной метрикой является наличие в этом пространстве счетной базы - но даже счетное регулярное пространство может быть не метризуемо. Простейший пример получается присоединением к дискретному натуральному ряду какой-нибудь одной точки из нароста Стоуна- Чеха бикомпактного расширения натурального ряда. Неожиданный характер носит критерий метризуемости метризуемого пространства Xполной метрикой - для этого необходимо и достаточно, чтобы Xбыло множеством типа Gd. в каком-нибудь (а тогда и в любом) бикомпактном хаусдорфовом расширении пространства X. Впрочем, бикомпактные хаусдорфовы расширения М. п. несут полную информацию о топологии последних, как это видно из теоремы Чеха: М. п. гомеоморфны в том и только в том случае, если гомеоморфны их расширения Стоуна - Чеха. стандартным образом связано другое М. п., а именно пространство
стандартным образом связано другое М. п., а именно пространство  всех его непустых замкнутых подмножеств, несущее на себе метрику Хаусдорфа, определяемую следующей формулой:
всех его непустых замкнутых подмножеств, несущее на себе метрику Хаусдорфа, определяемую следующей формулой:
 изометрично замкнутому подпространству полученного М. п.
изометрично замкнутому подпространству полученного М. п.  . Если метрика r полна, то и метрика
. Если метрика r полна, то и метрика  полна. Но из топологич. эквивалентности метрик
полна. Но из топологич. эквивалентности метрик  и
и  , заданных на X, не следует, вообще говоря, что отвечающие им метрики Хаусдорфа
, заданных на X, не следует, вообще говоря, что отвечающие им метрики Хаусдорфа  и
и 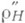 топологически эквивалентны.
топологически эквивалентны. метризуем, метрику, осуществляющую метризацию Y, не удается получить из метрики
метризуем, метрику, осуществляющую метризацию Y, не удается получить из метрики  посредством какой-либо формулы. Вместо метрики на
посредством какой-либо формулы. Вместо метрики на  по
по  естественно определяется функция dпосредством правила:
естественно определяется функция dпосредством правила: 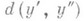 для любых
для любых  равно расстоянию в смысле р между прообразами точек
равно расстоянию в смысле р между прообразами точек  и
и 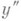 при рассматриваемом отображении. Часто (напр., если
при рассматриваемом отображении. Часто (напр., если  - пространство разбиения М. п. на компакты)
- пространство разбиения М. п. на компакты) хорошо согласуется с топологией Yи является симметрикой. Последнее означает, что
хорошо согласуется с топологией Yи является симметрикой. Последнее означает, что для всех
для всех 
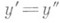 . Симметрика d, так определенная, почти никогда не удовлетворяет аксиоме треугольника, но если разбиение на компакты непрерывно, то dобладает топологич. свойствами, с успехом заменяющими аксиому треугольника и гарантирующими метризуемость образа "настоящей" метрикой.
. Симметрика d, так определенная, почти никогда не удовлетворяет аксиоме треугольника, но если разбиение на компакты непрерывно, то dобладает топологич. свойствами, с успехом заменяющими аксиому треугольника и гарантирующими метризуемость образа "настоящей" метрикой.