"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МЕТРИЧЕСКИЙ ТЕНЗОР
Значение МЕТРИЧЕСКИЙ ТЕНЗОР в математической энциклопедии:
основной тензор, фундаментальный тензор,- поле дважды ковариантного симметрич. тензора  на n-мерном дифференцируемом многообразии
на n-мерном дифференцируемом многообразии  . Задание на
. Задание на  М. т. вводит в касательном к
М. т. вводит в касательном к  в точке
в точке  векторном пространстве
векторном пространстве  скалярное произведение
скалярное произведение  контравариантных векторов
контравариантных векторов  определяемое как билинейная функция
определяемое как билинейная функция  где
где  - значение поля gв точке р. В координатной записи:
- значение поля gв точке р. В координатной записи:

Метрика пространства  с введенным в нем скалярным произведением принимается в бесконечно малом за метрику многообразия
с введенным в нем скалярным произведением принимается в бесконечно малом за метрику многообразия  , что выражается в выборе дифференциальной квадратичной формы
, что выражается в выборе дифференциальной квадратичной формы

квадратом дифференциала длины дуги кривой  , исходящей из рв направлении
, исходящей из рв направлении  По ее геометрич. смыслу форму (*) наз. метрической, или первой основной, формой на
По ее геометрич. смыслу форму (*) наз. метрической, или первой основной, формой на  ,
,
соответствующей М. т. g. Обратно, если на  задана симметрическая квадратичная форма вида (*), то ей сопоставляется поле дважды ковариантного тензора
задана симметрическая квадратичная форма вида (*), то ей сопоставляется поле дважды ковариантного тензора  соответствующая метрич. форма к-рого совпадает с g. Таким образом, задание на
соответствующая метрич. форма к-рого совпадает с g. Таким образом, задание на  М. т. g равносильно заданию на
М. т. g равносильно заданию на  метрики с квадратом линейного элемента вида (*). М. т. полностью определяет внутреннюю геометрию
метрики с квадратом линейного элемента вида (*). М. т. полностью определяет внутреннюю геометрию  Совокупность М. т. gи . определяемых ими метрик подразделяется на два класса - вырожденные метрики, когда
Совокупность М. т. gи . определяемых ими метрик подразделяется на два класса - вырожденные метрики, когда  и невырожденные, когда
и невырожденные, когда  . Многообразие
. Многообразие  с вырожденной метрикой (*) наз. изотропным. Среди невырожденных М. т., в свою очередь, различаются риманов М. т., для к-рого квадратичная форма (*) является положительно определенной, и псевдориманов М. т., когда форма (*) является знакопеременной. Риманова (псев-дориманова) метрика, вводимая на
с вырожденной метрикой (*) наз. изотропным. Среди невырожденных М. т., в свою очередь, различаются риманов М. т., для к-рого квадратичная форма (*) является положительно определенной, и псевдориманов М. т., когда форма (*) является знакопеременной. Риманова (псев-дориманова) метрика, вводимая на  через риманов (псевдориманов) М. т., определяет на
через риманов (псевдориманов) М. т., определяет на 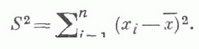 риманову (соответственно псевдориманову) геометрию.
риманову (соответственно псевдориманову) геометрию.
Обычно под М. т. без специального на то указания понимается риманов М. т.; но если, рассматривая невырожденный М. т., хотят подчеркнуть, что речь идет именно о римановом, а не псевдоримановом М. т., то об этом М. т. говорят как о собственно римановом М. т. Собственно риманов М. т. может быть введен на любом паракомпактном дифференцируемом многообразии.
Лит.:[1] Эйзенхарт Л. П., Риманова геометрия, пер. с англ., М., 1948; [2] Рашевский П. К., Риманова геометрия и тензорный анализ, 3 изд., М., 1967; [3] Громол Д., Клингенберг В., Мейер В., Риманова геометрия в целом, пер. с нем., М., 1971.
И. X. Сабитов.

 на n-мерном дифференцируемом многообразии
на n-мерном дифференцируемом многообразии  . Задание на
. Задание на  М. т. вводит в касательном к
М. т. вводит в касательном к  в точке
в точке  векторном пространстве
векторном пространстве  скалярное произведение
скалярное произведение  контравариантных векторов
контравариантных векторов  определяемое как билинейная функция
определяемое как билинейная функция  где
где  - значение поля gв точке р. В координатной записи:
- значение поля gв точке р. В координатной записи:
 с введенным в нем скалярным произведением принимается в бесконечно малом за метрику многообразия
с введенным в нем скалярным произведением принимается в бесконечно малом за метрику многообразия  , что выражается в выборе дифференциальной квадратичной формы
, что выражается в выборе дифференциальной квадратичной формы
 , исходящей из рв направлении
, исходящей из рв направлении  По ее геометрич. смыслу форму (*) наз. метрической, или первой основной, формой на
По ее геометрич. смыслу форму (*) наз. метрической, или первой основной, формой на  ,
, задана симметрическая квадратичная форма вида (*), то ей сопоставляется поле дважды ковариантного тензора
задана симметрическая квадратичная форма вида (*), то ей сопоставляется поле дважды ковариантного тензора  соответствующая метрич. форма к-рого совпадает с g. Таким образом, задание на
соответствующая метрич. форма к-рого совпадает с g. Таким образом, задание на  М. т. g равносильно заданию на
М. т. g равносильно заданию на  метрики с квадратом линейного элемента вида (*). М. т. полностью определяет внутреннюю геометрию
метрики с квадратом линейного элемента вида (*). М. т. полностью определяет внутреннюю геометрию  Совокупность М. т. gи . определяемых ими метрик подразделяется на два класса - вырожденные метрики, когда
Совокупность М. т. gи . определяемых ими метрик подразделяется на два класса - вырожденные метрики, когда  и невырожденные, когда
и невырожденные, когда  . Многообразие
. Многообразие  с вырожденной метрикой (*) наз. изотропным. Среди невырожденных М. т., в свою очередь, различаются риманов М. т., для к-рого квадратичная форма (*) является положительно определенной, и псевдориманов М. т., когда форма (*) является знакопеременной. Риманова (псев-дориманова) метрика, вводимая на
с вырожденной метрикой (*) наз. изотропным. Среди невырожденных М. т., в свою очередь, различаются риманов М. т., для к-рого квадратичная форма (*) является положительно определенной, и псевдориманов М. т., когда форма (*) является знакопеременной. Риманова (псев-дориманова) метрика, вводимая на  через риманов (псевдориманов) М. т., определяет на
через риманов (псевдориманов) М. т., определяет на 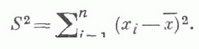 риманову (соответственно псевдориманову) геометрию.
риманову (соответственно псевдориманову) геометрию.