|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МАТЬЕ ГРУППАЗначение МАТЬЕ ГРУППА в математической энциклопедии: - конечная группа, изоморфная одной из пяти групп, открытых Э. Матьё [1]. Серия М. г. состоит из групп, обозначаемых
они представимы как группы подстановок на множествах из 11,12, 22, 23, 24 элементов соответственно. Группы М 12 и M24 являются пятикратно транзитивными. M11 реализуется естественным образом как стабилизатор в М 12 элемента множества, на к-ром действует М 12, М 23 - как стабилизатор элемента в M24 , М 22- как стабилизатор элемента в М 23. Порядки М. г. равны соответственно 7 920, 95 040, 443 520, 10 200 960, 244 823 040. При рассмотрении М. г. часто пользуются (см. [2]) представлением ее в виде группы автоморфизмов соответствующей системы Штейнера М. г. были первыми (и на протяжении более 80 лет единственными) известными спорадическими конечными простыми группами. Лит.:[1] Mathieu Ё., "J. math, pures et appl.", 1861, t. 6, p. 241 - 323; 1873, t. 18, p. 25-46; [2] Witt E., "Abhandl. Math. Semin. Univ. Hamburg", 1938, Bd 12, S. 256-64, 265-75; [3] Итоги науки и техники. Алгебра. Топология. Геометрия, т. 14, М., 1976, с. 5-56. С. П. Струннов. |
|
|
|
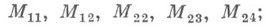
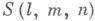, т. е. множества из пэлементов, в к-ром выделена система 
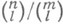подмножеств, называемых блоками, состоящих из тэлементов множества, причем каждые lэлементов содержатся в одном и только в одном блоке. Автоморфизмом системы Штейнера наз. подстановка множества ее элементов, переводящая блок в блок. Группа М 11 является группой автоморфизмов системы Штейнера 
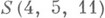, группа М 12 - системы S(5, 6, 12), группа М 22 - системы S(3, 6, 22), группа М 23 - системы 5(4, 7, 23), группа M24- системы S(5, 8, 24).