"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
АСИМПТОТИЧЕСКИ НЕСМЕЩЕННАЯ ОЦЕНКАЗначение АСИМПТОТИЧЕСКИ НЕСМЕЩЕННАЯ ОЦЕНКА в математической энциклопедии:
понятие, утверждающее несмещенность оценки в пределе (см. Несмещенная оценка). Пусть  - последовательность случайных величин на вероятностном пространстве - последовательность случайных величин на вероятностном пространстве  , где Ресть одна из мер семейства , где Ресть одна из мер семейства  . На семействе . На семействе  задан функционал задан функционал  и имеется последовательность S-измеримых функций и имеется последовательность S-измеримых функций 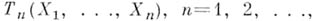 математич. ожидания к-рых математич. ожидания к-рых  существуют. Тогда, если при существуют. Тогда, если при 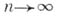 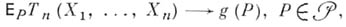
говорят, что  есть функция, асимптотически несмещенная для функционала есть функция, асимптотически несмещенная для функционала  Называя Называя  наблюдениями и наблюдениями и  оценкой, получают определение А, н. о. В простейшем случае неограниченного повторного выбора из совокупности, распределение к-рой содержит одномерный параметр оценкой, получают определение А, н. о. В простейшем случае неограниченного повторного выбора из совокупности, распределение к-рой содержит одномерный параметр  , А. н. о. , А. н. о.  для для  , построенная по выборке объема п, удовлетворяет , построенная по выборке объема п, удовлетворяет 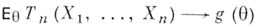 условию для каждого условию для каждого 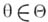 , Когда , Когда  . О. В. Шалаевский. . О. В. Шалаевский.
|

 - последовательность случайных величин на вероятностном пространстве
- последовательность случайных величин на вероятностном пространстве  , где Ресть одна из мер семейства
, где Ресть одна из мер семейства  . На семействе
. На семействе  задан функционал
задан функционал  и имеется последовательность S-измеримых функций
и имеется последовательность S-измеримых функций 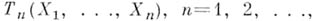 математич. ожидания к-рых
математич. ожидания к-рых  существуют. Тогда, если при
существуют. Тогда, если при 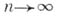
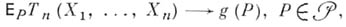
 есть функция, асимптотически несмещенная для функционала
есть функция, асимптотически несмещенная для функционала  Называя
Называя  наблюдениями и
наблюдениями и  оценкой, получают определение А, н. о. В простейшем случае неограниченного повторного выбора из совокупности, распределение к-рой содержит одномерный параметр
оценкой, получают определение А, н. о. В простейшем случае неограниченного повторного выбора из совокупности, распределение к-рой содержит одномерный параметр  , А. н. о.
, А. н. о.  для
для  , построенная по выборке объема п, удовлетворяет
, построенная по выборке объема п, удовлетворяет 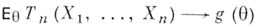 условию для каждого
условию для каждого 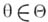 , Когда
, Когда  . О. В. Шалаевский.
. О. В. Шалаевский.