|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МАТРИЦ КОЛЬЦОЗначение МАТРИЦ КОЛЬЦО в математической энциклопедии: полное кольцо матриц,- кольцо всех квадратных матриц фиксированного порядка над кольцом R. Кольцо Кольцо Rn изоморфно кольцу End Mвсех эндоморфизмов свободного правого R-модуля М, обладающего га-элементным базисом. Матрица единица в Rn. Ассоциативное кольцо А с единицей 1 тогда и только тогда изоморфно Rn, когда в Аесть множество из n2 элементов 1) 2) централизатор множества элементов е ij в Аизоморфен кольцу R. Центр кольца Rn совпадает с Z(R)En, где Z(R)- центр R;при n>1 кольцо Rn некоммутативно. Мультипликативная группа кольца Rn (группа всех обратимых элементов) наз. полной линейной группой и обозначается GL(n, R). Матрица из Rn обратима в Rn тогда и только тогда, когда ее столбцы составляют базис свободного правого модуля всех Кольцо Rn тогда и только тогда просто, когда просто R , ибо двусторонние идеалы в Rn имеют вид к n , где к- двусторонний идеал в R. Артиново кольцо тогда и только тогда просто, когда оно изоморфно М. к. над телом (теорема Веддерберна - Артина). категория R-модулей эквивалентна категории Rn -модулей. Однако из того, что проективные R-модули свободны, еще не следует, что будут свободны и проективные Rn -модули. Так, если R- поле, а n>1, то существуют несвободные конечно порожденные проективные Rn -модули. Лит.:[1] Фейс К., Алгебра: кольца, модули и категории, пер. с англ., т. 1, М., 1977; [2] Ламбек И., Кольца и модули, пер. с англ., М., 1971; [3] Бокуть Л. А., Ассоциативные кольца, ч. 1, Новосиб., 1977. Д. А. Супруненко. |
|
|
|
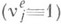-матриц над R обозначается Rn или Mn(R). Всюду ниже R- ассоциативное кольцо с единицей 1.
-
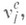подчиненное следующим условиям:
-матриц над R. Если R коммутативно, то обратимость матрицы ав Rn равносильна обратимости ее определителя det ав R. Имеет место равенство 
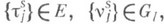
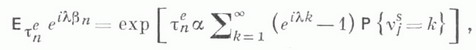где J(R) - радикал Джекобсона кольца R. Следовательно, для полупростого кольца R М. к. над R также полупросто. Если R регулярно (т. е. для любого 
в R есть такое b, что аbа=а), то и Rn регулярно. Если R - кольцо с инвариантным базисным числом, т. е. число базисных элементов каждого свободного R-модуля не зависит от выбора базиса, то Rn также кольцо с инвариантным базисным числом. Кольца R и Rn эквивалентны в смысле Мориты (см. Мориты эквивалентность):